Алгоритмы растеризации отрезков, окружностей и эллипсов
3.4. Изображение окружностей
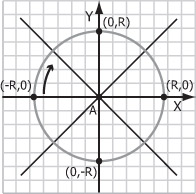
Для начала перейдем к канонической системе координат, в которой центр окружности совпадает с началом координат. Тогда можно заметить, что в силу симметрии окружности относительно прямых, разделяющих октанты, достаточно построить растровое представление в одном октанте, а затем с помощью симметрий получить изображения в других октантах (см. рис. 3.7). Будем пользоваться заданием окружности в виде неявной функции: x2 + y2 - R2 = 0.
Пусть f(x, y) = x2 + y2 - R2. Будем рисовать часть окружности в 4 -м октанте, начиная с точки (-R, 0) (см. рис. 3.7, показано стрелкой).
Пусть  , тогда
, тогда  . Пусть функция plot8(x, y) отображает на растре все 8 точек, полученных из (x, y) с помощью симметрий.
. Пусть функция plot8(x, y) отображает на растре все 8 точек, полученных из (x, y) с помощью симметрий.
Алгоритм Брезенхема
Будем рассуждать подобно алгоритму Брезенхема для отрезков (с соответствующими поправками на 4 -й октант) [17]. Из двух возможных пикселов в 4 -м октанте (соответствующих вертикальному и диагональному смещениям, которые обозначаются аналогично прежним s и d, см. рис. 3.10) будем выбирать тот, расстояние от окружности до которого меньше.
Для того чтобы выбрать один из двух возможных пикселей, будем сравнивать расстояния от них до окружности: где расстояние меньше - тот пиксел и будет искомым. В примере на рис. 3.8 сравниваются расстояния от точек S(xs, ys) и D(xd, yd) до окружности с радиусом R. Из евклидовой метрики получаем:
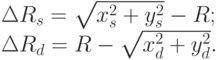
Но вычисление квадратного корня - вычислительно трудоемкая операция, поэтому при достаточно больших R мы будем заменять сравнение расстояний сравнением приближенных значений их квадратов (см. рис. 3.9):
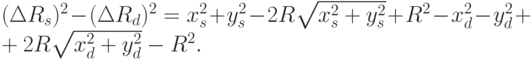
Уменьшим два слагаемых на приблизительно одинаковые величины:
 заменим на
заменим на  ,
,
 заменим на
заменим на 
получим

Таким образом, приближенно
-
D ближе к окружности, чем S


-
S ближе к окружности, чем D


Пусть (x, y) - текущий пиксель. Обозначим

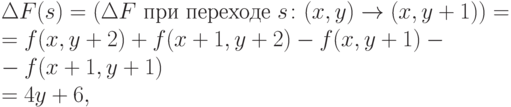
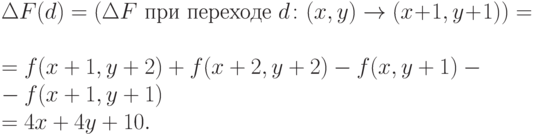
Тогда из двух возможных смещений d и s выберем.
-
 , т.е. (x + 1, y + 1) ближе к
окружности, чем (x, y + 1):
, т.е. (x + 1, y + 1) ближе к
окружности, чем (x, y + 1):d: Переходим в (x + 1, y + 1) и придаем соответствующие приращения F,
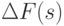 ,
, 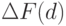 :
: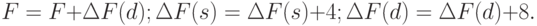
-
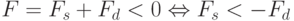 , т.е. (x, y+1) ближе к окружности,
чем (x + 1, y + 1):
, т.е. (x, y+1) ближе к окружности,
чем (x + 1, y + 1):s: Переходим в (x, y + 1) и придаем соответствующие приращения F,
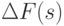 ,
, 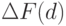 :
:
Если мы начинаем из (-R, 0), то начальные значения будут следующими:
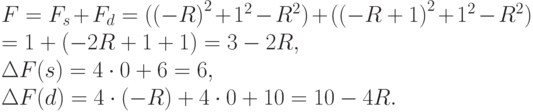
Легко видеть, что в алгоритме все величины, связанные с F, кроме F начального, будут кратны 2. Но, если мы поделим все эти величины на 2 (в дальнейшем значения всех величин уже понимаются в этом смысле), то  . Так как приращения F могут быть только целочисленными, то
. Так как приращения F могут быть только целочисленными, то  , где
, где 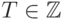 ; т.е. если отнять
; т.е. если отнять  от всех значений, то знак F не изменится для всех T, кроме T = 0. Для того чтобы результат сравнения остался прежним, будем считать, что F = 0 теперь соответствует смещению s.
от всех значений, то знак F не изменится для всех T, кроме T = 0. Для того чтобы результат сравнения остался прежним, будем считать, что F = 0 теперь соответствует смещению s.
x = -r; y = 0;
F = 1-r;
delta_Fs = 3;
delta_Fd = 5-2*r;
while( x + y < 0 )
{
plot8( x, y );
if( F > 0 )
{
// d: Диагональное смещение
F += delta_Fd;
x++; y++;
delta_Fs += 2;
delta_Fd += 4;
}
else
{
// s: Вертикальное смещение
F += delta_Fs;
y++;
delta_Fs += 2;
delta_Fd += 2;
}
}
Листинг
3.5.
Алгоритм Брезенхема для окружности
Размерность вычислений этого алгоритма (т.е. отношение максимальных модулей значений величин, с которыми он оперирует к модулям исходных данных (в данном случае R )) равна 2.