Основные понятия. Представление цвета в машинной графике
Преобразования между CIE XYZ и RGB
Цветовое пространство RGB, как и CIE XYZ, является трехмерным и аддитивным. Поэтому преобразования между двумя этими пространствами описываются матрицами 3 x 3 ; достаточно задать координаты базисных цветов R, G и B в системе CIE XYZ. Обычно удобно это делать, отдельно задавая цветовую информацию точками (x, y) на диаграмме цветности и яркостной компонентой Y. Если цвет задан таким образом (x, y, Y), то из формул (1.1) следует, что
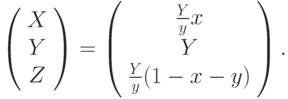 |
( 1.2) |
Тогда, если базисные RGB-цвета заданы как (xR, yR, YR), (xG, yG, YG), (xB, yB, YB), получаем следующую формулу преобразования:
zR=1-xR-yR; zG=1-xG-yG; zB=1-xB-yB;1.1. Переход от RGB к CIE XYZ
![\left( \begin{array}{c}
X \\
Y \\
Z
\end{array} \right) ={ \left[ \begin{array}{ccc}
\frac{Y_R}{y_R}x_R & \frac{Y_G}{y_G}x_G & \frac{Y_B}{y_B}x_B \\
Y_R & Y_G & Y_ B \\
\frac{Y_R}{y_R}z_R & \frac{Y_G}{y_G}z_G & \frac{Y_B}{y_B}z_B
\end{array} \right] \left( \begin{array}{c}
R \\
G \\
B
\end{array} \right) };](/sites/default/files/tex_cache/21b832a162feeb62a0430fa0285b4fa7.png)
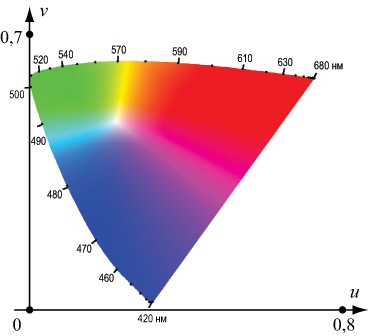
Все представимые в модели RGB цвета образуют параллелепипед в CIE XYZ (см. рис. 1.10), пересечение которого с плоскостью X + Y + Z = 1, спроецированное на диаграмму цветности и дает цветовую гамму данной модели.
Таким образом, в зависимости от координат (x, y, Y ) для базисных цветов в конкретном устройстве (фотоаппарате, мониторе, проекторе и т.п.) одним и тем же значениям (R,G,B) соответствуют разные цвета.
Цветовые пространства, в которых каждому набору цветовых компонент соответствует физически единственный цвет, называются абсолютными цветовыми пространствами. Таким пространством является как раз CIE XYZ. Если мы также однозначно зафиксируем (x, y, Y ) для базисных RGB-цветов, то получим абсолютное RGB-пространство. Такие стандартные пространства играют важную роль в обеспечении одинакового отображения одного и того же изображения на разных устройствах. Для корректного отображения на конкретном устройстве изображение надо перевести из абсолютного пространства в цветовое пространство для данного устройства. Для осуществления подобного преобразования программным путем информация о характеристиках устройства хранится в сопоставленном ему специальном файле. Стандарт на такие файлы был разработан ICC (англ. International Color Consortium), поэтому они получили название профилей ICC.
Наиболее широко распространенным абсолютным RGB-пространством является модель sRGB (хорошо отражает характеристики цифровых фотокамер любительского уровня), также были созданы Adobe RGB, AdobeWide Gamut RGB и ProPhoto RGB, каждая последующая с все более широкой цветовой гаммой для представления максимальной части цветов видимого спектра. В ProPhoto RGB "базисные цвета" R, G и B ради этого даже находятся за рамками зоны видимых цветов. Для представления цветов в таком широком диапазоне рекомендуется использовать повышенную точность с 16 или более бит/канал. Все эти модели представлены на рис. 1.11.
Цветовые модели CIE L*u*v* и CIE L*a*b*
У модели CIE XYZ все же есть существенный недостаток - неоднородность восприятия изменения цвета относительно расстояния на диаграмме цветности. В идеале хотелось бы, чтобы одинаковые расстояния между точками, соответствующими цветам на диаграмме цветности, соответствовали приблизительно одинаковому восприятию человеком отличий между этими парами цветов. Именно для этих целей CIE в 1976 году предложила модель L*u*v*. L* (от англ. Lightness) в этой модели соответствует яркости, скорректированной с учетом особенностей человеческого восприятия [21]. Получающаяся диаграмма цветности представлена на рис. 1.12. Эта модель рекомендуется для представления света от источников.
Определим функцию F(s) как
 |
( 1.3) |
и определим
u' = 4X/(X + 15Y + 3Z); v' = 9Y/(X + 15Y + 3Z);
Пусть точка белого имеет координаты (Xw, Yw, Zw), тогда получим следующий алгоритм преобразования:
L* = 116F(Y/Yw) - 16; u* = 13L*(u' - u'w); v* = 13L*(v' - v'w);Листинг 1.2. Переход от XYZ к L*u*v*
В обратную сторону:
u' = u*/(13L*) + u'w; v' = v*/(13L*) + v'w; Y = F-1((L* + 16)/116)Yw; X = 9Yu'/4v'; Z = (4X - 15v'Y - v'X)/3u';Листинг 1.3. Переход от L*u*v* к XYZ
Также CIE в 1976 году с той же целью предложила и другую похожую модель L*a*b*, которая получила несколько более широкое распространение [21]. Эта модель рекомендуется для представления отраженного света.
В ней используется та же функция F(s), определенная в (1.3), и L* имеет то же самое значение, что в L*u*v*.
L* = 116F(Y/Yw) - 16; a* = 500[F(X/Xw) - F(Y/Yw)]; b* = 200[F(Y/Yw) - F(Z/Zw)];Листинг 1.4. Переход от XYZ к L*a*b*