НОУ ИНТУИТ | Алгоритмические основы растровой графики. Лекция 7: Дискретизация. Антиалиасинг. Геометрические преобразования растровых изображений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 23.04.2007 | Доступ: свободный | Студентов: 3322 / 463 | Оценка: 4.18 / 3.71 | Длительность: 17:54:00

ISBN: 978-5-9556-0098-7

Тема: Компьютерная графика

Специальности: Программист

|

Вам нравится? Нравится 37 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Теорема Найквиста-Котельникова

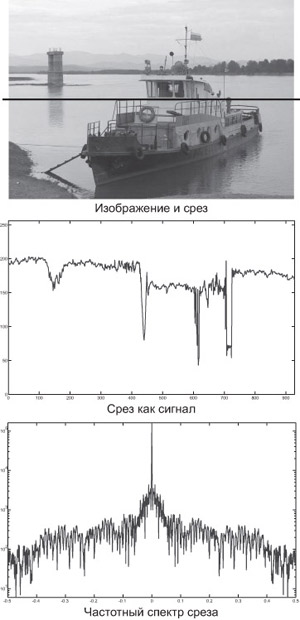
Теорема Найквиста-Котельникова дает ответ на вопрос, какой частоты дискретизации f_s достаточно для того, чтобы не произошло потери информации, т.е. чтобы по дискретизованному сигналу можно было восстановить исходный. Применительно к изображениям это грубо (поскольку еще не ясно, как происходит восстановление, которое зависит от устройства отображения) можно понимать так: "Какая разрешающая способность должна быть у растра, чтобы он сохранил все детали исходного аналогового изображения". Хотя потеря информации даже в случае соблюдения условий теоремы Котельникова произойдет из-за того, что значения дискретизованной функции (растрового изображения) в компьютере сами хранятся с ограниченной точностью. Передача цветов и оттенков лучшим образом при ограниченном диапазоне значений является задачей квантования, которая рассмотрена в "Алгоритмы квантования для полутоновых и цветных изображений" .

Рис. 7.2. Срез изображения как сигнал и его частотный спектр.

Рис. 7.3. Гребенчатый фильтр и его преобразование Фурье.

В доказательстве теоремы и далее будет использоваться операция свертки функций I(x), J(x), определяемая так:

$(I * J)(x) \stackrel{def}{ = }\int_{-\infty}^{\infty} I(u) \cdot J(x - u)du.$

Теорема 7.1.1 (Найквиста-Котельникова). Для того чтобы сигнал I(x) можно было восстановить по его дискретному образу, его спектр должен быть ограничен максимальной частотой f_H и частота дискретизации f_s должна быть более 2f_H.

Доказательство использует факты из математического и функционального анализа (см. например [3]). Пусть I_s(x) - дискретный образ исходного сигнала I(x), как обычно, T = 1/f_s - период дискретизации, тогда

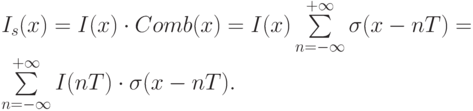
$I_s(x) = I(x)\cdot Comb(x) = I(x) \sum\limits_{n=-\infty}^{+\infty}\sigma (x-nT) = \\ \sum\limits_{n=-\infty}^{+\infty}I(nT)\cdot \sigma (x-nT).$

Образом функции Comb в частотной области является функция

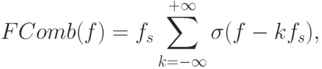
$FComb(f) = f_s \sum\limits_{k=-\infty}^{+\infty}\sigma (f - kf_s),$

а Фурье-образ I(x) по-прежнему будем обозначать F(f). Умножение функций в пространственной области соответствует их свертке (будем обозначать ее ) в частотной и наоборот. Соответственно, рассмотрим свертку F и FComb, являющуюся Фурье-образом I_s(x) (обозначим его F_s(f) ):

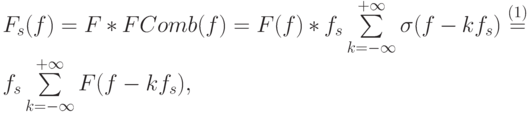$F_s(f) = F * FComb(f) = F(f) * f_s \sum\limits_{k=-\infty}^{+\infty}\sigma (f - kf_s) \stackrel{(1)}{ = } \\ f_s \sum\limits_{k=-\infty}^{+\infty}F(f-kf_s),$

( 7.6)

где переход (1) произошел благодаря сдвигающему свойству дельта-функции при свертке. Как видно из последнего выражения, F_s(f) представляет собой бесконечную сумму функций F(f), умноженных на f_s и сдвинутых на f_s относительно друг друга, поэтому при условии f_s > 2f_H носители соседних сдвинутых версий не пересекаются, и отдельно, взяв центральную копию F(f) (k = 0) и применив к ней обратное преобразование Фурье, можно получить исходный сигнал I(x). Центральная копия берется путем умножения F_s(f) на прямоугольную функцию 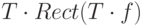$T \cdot Rect(T \cdot f)$ , где

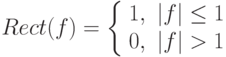
$Rect(f) =\left\{ \begin{array}{cc} 1, & |f| \le 1 \\ 0, & |f| > 1 \\ \end{array} \right.$

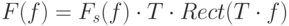Т.е. $F(f) = F_s(f) \cdot T \cdot Rect(T \cdot f)$ , - образ исходной функции получен. Заметим, этому умножению в частотной области соответствует свертка в пространственной области. Применив обратное преобразование Фурье к 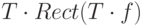$T \cdot Rect(T \cdot f)$ , получим функцию

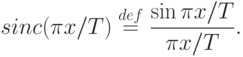$sinc(\pi x/T)\stackrel{def}{ = }\frac{\sin \pi x/T}{\pi x/T}.$

( 7.7)

Применив свертку с I_s(x), получаем

$I(x) = I_s(x) * sinc(\pi x/T) \\ = \sum\limits_{n=-\infty}^{+\infty}\left( I(nT) \cdot \sigma (x - nT)\right) * sinc((x - nT)/T) \\ \stackrel{(2)}{ = }\sum\limits_{n=-\infty}^{+\infty}I(nT) \cdot sinc((x - nT)/T),$

где переход (2) также произошел благодаря сдвигающему свойству дельта-функции при свертке. Последняя формула называется Интерполяционной формулой Найквиста-Шеннона.

Для завершения доказательства осталось показать, что невозможно однозначно восстановить сигнал при 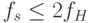$f_s \le 2f_H$ .

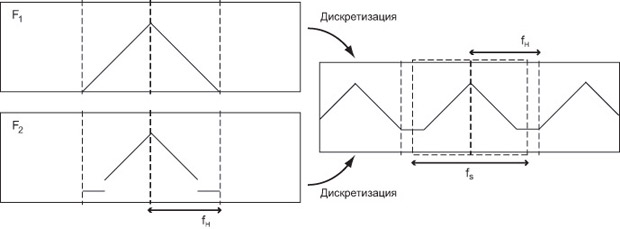
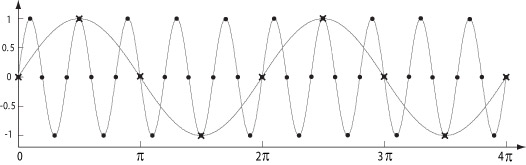
Приведем соответствующий пример. Зафиксируем две частоты - f_s и f_H, 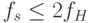$f_s \le 2f_H$ ; для упрощения рассуждений предположим, что f_s > f_H (в общем случае может быть более двух наложений сдвинутых образов, что усложнит построение контрпримера). Из формулы (7.6) следует, что Фурье-образ I_s(x) является периодической функцией с периодом f_s, поэтому вся информация для восстановления содержится в одном периоде (например $f \in [-\frac{f_s}{2}, \frac{f_s}{2}]$ ). Рассмотрим две функции, Фурье-образы которых равны

$F_1(f) =\left\{ \begin{array}{ccc} f_H - |f|, & |f| \in [0, f_s - f_H) \\ \frac{2f_H-f_s}{2}, & |f| \in [f_s - f_H, f_H] \\ 0, & |f| > f_H \\ \end{array} \right.$

$F_2(f) = \left\{ \begin{array}{cc} f_H - |f|, & |f| \in [0, f_H] \\ 0, & |f| > f_H \\ \end{array} \right.$

(функция однозначно задается своим Фурье-образом). При дискретизации с частотой f_s в соответствии с формулой (7.6) Фурье-образ в интервале $[-\frac{f_s}{2}, \frac{f_s}{2}]$ для обеих функций будет равен

$F_s(f) = \left\{ \begin{array}{cc} f_s(f_H - |f|), & |f| \in [0, f_s - f_H) \\ f_s(2f_H - f_s), & |f| \in [f_s - f_H, f_s/2] \\ \end{array} \right.$

(см. рис. 7.4).

Таким образом, в этом случае однозначная реконструкция невозможна.

увеличить изображение
Рис. 7.4. Пример двух функций, дискретизированный образ которых совпадает

Рис. 7.5. Адекватная и неадекватная частоты дискретизации

Дальше >>

Авторизоваться

Алгоритмические основы растровой графики

Дискретизация. Антиалиасинг. Геометрические преобразования растровых изображений

Теорема Найквиста-Котельникова

Вопросы и ответы