Преобразование автомата для упрощения функционального контроля
Необходимость в таком преобразовании возникает при решении проблемы повышения надежности цифровых устройств (ЦУ). Решение упомянутой проблемы в качестве обязательного этапа включает обнаружение неисправности в ЦУ, поскольку лишь после установления факта отказа ЦУ имеет смысл проводить работы по восстановлению его правильного функционирования. Существующие методы контроля ЦУ подразделяются на тестовые и функциональные. Каждый из них имеет свои достоинства и недостатки. Ниже речь будет идти о реализации функционального контроля, который требует некоторых аппаратурных затрат, что является его недостатком, но осуществляется в процессе использования ЦУ по его прямому назначению, что относится к несомненным достоинствам.
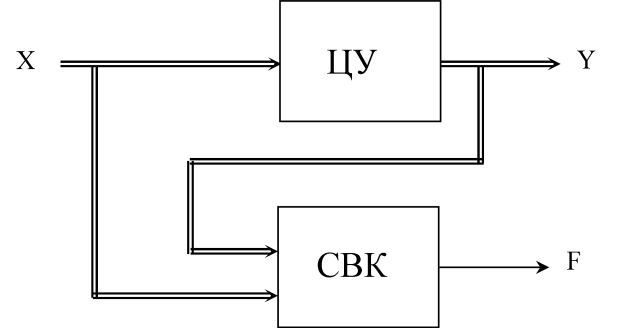
Обычно функциональный контроль реализуется так, как это изображено на рис.9.1. На этом рисунке блок СВК представляет собой схему встроенного контроля. Как видно из рисунка, рабочие воздействия  поступают как на ЦУ, так и на СВК. Помимо последовательности
поступают как на ЦУ, так и на СВК. Помимо последовательности  на входы СВК поступают также выходные реакции
на входы СВК поступают также выходные реакции  ЦУ. На выход
ЦУ. На выход  СВК выводится информация о техническом состоянии (исправности или неисправности) ЦУ.
СВК выводится информация о техническом состоянии (исправности или неисправности) ЦУ.
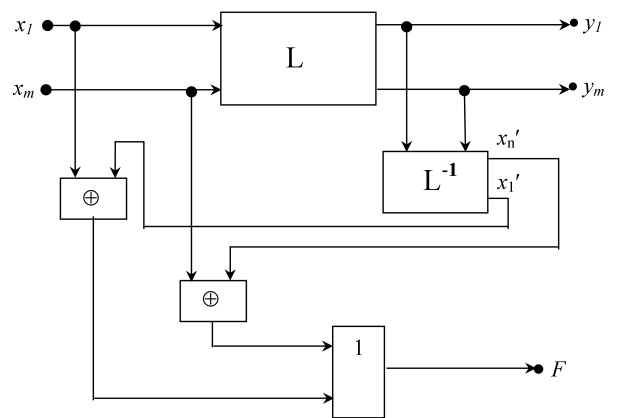
Один из принципов построения СВК для комбинационных устройств (КУ), используемый на практике, базируется на восстановлении входов ЦУ (рис.9.2).
Известно, что для КУ блок 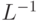 существует не всегда, а необходимым и достаточным условием его существования является наличие у булевых функций, реализуемых блоком
существует не всегда, а необходимым и достаточным условием его существования является наличие у булевых функций, реализуемых блоком  , свойства обратимости [80].
, свойства обратимости [80].
Аналогичный принцип построения СВК может быть использован и для устройств с памятью, описываемых математической моделью автомата Мили.
В лекции 4 был рассмотрен класс ОБПИК-автоматов, которые обладают следующим свойством: по наблюдаемой реакции такого автомата на неизвестную входную последовательность длины  всегда возможно однозначное восстановление первого символа этой входной последовательности независимо от начального состояния автомата из заданного множества
всегда возможно однозначное восстановление первого символа этой входной последовательности независимо от начального состояния автомата из заданного множества  допустимых состояний. Отметим, что упомянутое восстановление осуществляется с помощью специальной схемы, описанной в лекции 4, которая фактически является СВК, изображенной на рис.9.2. Существенный недостаток использования упомянутой СВК при
допустимых состояний. Отметим, что упомянутое восстановление осуществляется с помощью специальной схемы, описанной в лекции 4, которая фактически является СВК, изображенной на рис.9.2. Существенный недостаток использования упомянутой СВК при  состоит в том, что сигнал на ее выходе
состоит в том, что сигнал на ее выходе 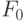 возникшей неисправности в ЦУ появится не в момент ее первого проявления, а через
возникшей неисправности в ЦУ появится не в момент ее первого проявления, а через  тактов. Понятно, что такая задержка может привести к катастрофическому отказу ЦУ. Таким образом, чтобы исключить такую ситуацию, необходимо, чтобы порядок
тактов. Понятно, что такая задержка может привести к катастрофическому отказу ЦУ. Таким образом, чтобы исключить такую ситуацию, необходимо, чтобы порядок  ОБПИК-автомата был равен 1.
ОБПИК-автомата был равен 1.
В связи с изложенным возникает задача преобразования произвольного автомата в ОБПИК-автомат порядка 1, которая и будет исследована в этом разделе.
Указанное преобразование будем осуществлять за счет расширения выходного алфавита автомата, достигаемого путем выведения контрольных точек.
Рассмотрим слабоинициальный минимальный автомат Мили 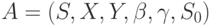 , где
, где  - множество допустимых начальных состояний
- множество допустимых начальных состояний  .
.
Как следует из теоремы 4.1, необходимое и достаточное условие принадлежности автомата классу ОБПИК порядка 1 состоит в следующем: в его проверочном графе, конструкция которого описана в лекции 4, должны отсутствовать выделенные дуги.
Легко показать, что выведение контрольных точек из автомата  , преобразующее его в ОБПИК-автомат порядка 1, эквивалентно нахождению такого разбиения
, преобразующее его в ОБПИК-автомат порядка 1, эквивалентно нахождению такого разбиения 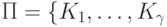 множества
множества 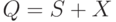 , чтобы проверочный граф автомата
, чтобы проверочный граф автомата 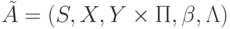 не имел выделенных дуг. Функция выходов в автомате
не имел выделенных дуг. Функция выходов в автомате 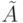 такова, что
такова, что 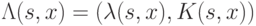 , где
, где  - код класса разбиения
- код класса разбиения  , содержащего пару
, содержащего пару  в некотором стандартном алфавите.
в некотором стандартном алфавите.
В формулировке рассматриваемой задачи отсутствует требование минимальности множества контрольных точек, поскольку при его наличии никакого другого метода ее решения, кроме перебора, не существует. Справедливость последнего утверждения вытекает из того, что задача поиска минимального множества контрольных точек может быть сведена к классической задаче о покрытии, относящейся к числу 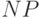 -полных проблем.
-полных проблем.
Напомним, что дуга 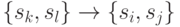 с пометкой
с пометкой  проверочного графа
проверочного графа  автомата
автомата  называется выделенной, если
называется выделенной, если

Очевидно, что в проверочном графе выделенные дуги имеются тогда и только тогда, когда один и тот же выходной сигнал встречается не менее чем в двух различных столбцах таблицы переходов-выходов (ТПВ) автомата. Следующая лемма дает возможность оценить количество выделенных дуг в проверочном графе автомата.
Лемма 9.1. Пусть символ  находится в
находится в  клетках ТПВ автомата
клетках ТПВ автомата  , а
, а 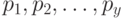 - номера всех столбцов ТПВ, которые этот символ содержат. Если
- номера всех столбцов ТПВ, которые этот символ содержат. Если 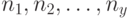 - количество символов
- количество символов  в соответствующих столбцах, то число выделенных дуг в проверочном графе автомата
в соответствующих столбцах, то число выделенных дуг в проверочном графе автомата  , помеченных символом
, помеченных символом  , равно величине
, равно величине
 |
( 9.1) |
где 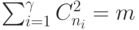 и
и 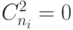 , если
, если 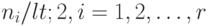 .
.
Доказательство приведенной формулы достаточно очевидно, поэтому мы не будем на нем останавливаться.
Вернемся теперь к рассматриваемой задаче отыскания множества выходных контрольных точек. По построению каждой выделенной дуге 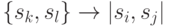 с пометкой
с пометкой  графа
графа  соответствует две дуги:
соответствует две дуги:  и
и 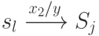 графа автомата
графа автомата  , которые далее именуются ее составляющими. Очевидно, что если изменить выходной сигнал
, которые далее именуются ее составляющими. Очевидно, что если изменить выходной сигнал  одной из этих дуг, то в проверочном графе для автомата с измененной функцией выхода эта выделенная дуга будет отсутствовать. Воспользуемся этим для удаления всех выделенных дуг в проверочном графе.
одной из этих дуг, то в проверочном графе для автомата с измененной функцией выхода эта выделенная дуга будет отсутствовать. Воспользуемся этим для удаления всех выделенных дуг в проверочном графе.
Опишем теперь способ получения разбиения  множества
множества 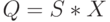 . С этой целью сначала сформируем список
. С этой целью сначала сформируем список  всех выделенных дуг в проверочном графе
всех выделенных дуг в проверочном графе  автомата
автомата  , упорядочив его произвольным образом. На основе списка
, упорядочив его произвольным образом. На основе списка  составим множество
составим множество 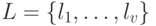 всех попарно различных дуг графа автомата
всех попарно различных дуг графа автомата  , являющихся составляющими выделенных дуг этого списка. Далее сформируем множество
, являющихся составляющими выделенных дуг этого списка. Далее сформируем множество  всех таких пар дуг автомата, которые совместно не образуют выделенной дуги проверочного графа. Содержательно принадлежность пары
всех таких пар дуг автомата, которые совместно не образуют выделенной дуги проверочного графа. Содержательно принадлежность пары  множеству
множеству  означает, что в автомате
означает, что в автомате  , полученном из
, полученном из  в результате расширения выходного алфавита, дуги
в результате расширения выходного алфавита, дуги 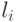 и
и 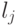 могут иметь одну и ту же пометку. Вместе с тем, если
могут иметь одну и ту же пометку. Вместе с тем, если 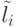 и
и 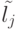 принадлежат разным парам из
принадлежат разным парам из  , то их пометки обязательно должны быть различными.
, то их пометки обязательно должны быть различными.
В принятых обозначениях алгоритм получения искомого разбиения  можно сформулировать следующим образом:
можно сформулировать следующим образом:
-
 .
. -
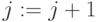 .
. - Проверка: выполняется ли неравенство
 ? Если нет, то переходим к пункту 4, предварительно положив
? Если нет, то переходим к пункту 4, предварительно положив 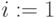 , иначе переходим к пункту 7.
, иначе переходим к пункту 7. - Для всех элементов
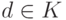 проверяется условие: принадлежит ли
проверяется условие: принадлежит ли  множеству
множеству  ? Если условие выполняется для всех
? Если условие выполняется для всех 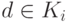 , то
, то 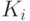 пополняем дугой
пополняем дугой 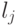 и переходим к пункту 2, в противном случае переходим
к пункту 5.
и переходим к пункту 2, в противном случае переходим
к пункту 5. -
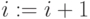 .
. - Проверка:
 ? Если да, то класс
? Если да, то класс 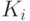 пополняем дугой
пополняем дугой 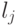 и переходим к пункту 2, иначе - к пункту 4.
и переходим к пункту 2, иначе - к пункту 4. - Конец работы алгоритма.
Проиллюстрируем описанный способ на примере. Пусть автомат  , у которого
, у которого  , задан своей ТПВ ( табл.9.1), в которой имеется
, задан своей ТПВ ( табл.9.1), в которой имеется  клеток
клеток  помеченных одним и тем же выходным символом
помеченных одним и тем же выходным символом  , причем в первом столбце имеется
, причем в первом столбце имеется 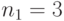 таких символов, во втором -
таких символов, во втором - 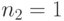 и в третьем -
и в третьем -  . В соответствии с леммой 9.1 общее число выделенных дуг этого автомата равно
. В соответствии с леммой 9.1 общее число выделенных дуг этого автомата равно  .
.
Приведем список  этих выделенных дуг, каждая из которых имеет одну и ту же пометку
этих выделенных дуг, каждая из которых имеет одну и ту же пометку  .
.
Множество всех попарно различных составляющих выделенных дуг этого списка есть 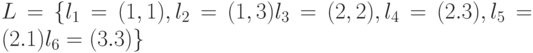 . Сформируем теперь на основе
. Сформируем теперь на основе  множество пар дуг
множество пар дуг 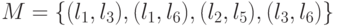 .
.
Применение предложенного алгоритма дает следующее разбиение  :
: 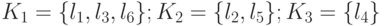 .
.
Поскольку разбиение имеет три класса, для кодирования символов классов достаточно двух двоичных переменных. Пусть  , тогда автомат с контрольными точками представлен табл.9.2.
, тогда автомат с контрольными точками представлен табл.9.2.
 |
0 | 1 | 2 |
|---|---|---|---|
| 1 | 1, a 0 0 | 2, b 0 0 | 3, a 1 0 |
| 2 | 2, a 0 0 | 3, a 0 1 | 1, a 1 0 |
| 3 | 3, a 0 0 | 1, b 0 0 | 2, c 0 0 |
Предположим, что выходные сигналы 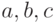 закодированы двоичными числами 00, 01 и 10. При таком кодировании часть СВК для рассматриваемого автомата, восстанавливающая входные сигналы, должна, как легко сообразить, реализовывать две булевы функции
закодированы двоичными числами 00, 01 и 10. При таком кодировании часть СВК для рассматриваемого автомата, восстанавливающая входные сигналы, должна, как легко сообразить, реализовывать две булевы функции 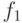 и
и  , заданные табл.9.3.
, заданные табл.9.3.
Отметим, что класс автоматов без потери информации конечного порядка 1 представляет собой важный частный случай, широко используемый в теории кодирования и получивший название взаимно однозначных автоматов. По аналогии, рассмотренные выше ОБПИК-автоматы порядка 1 назовем сильно взаимно однозначными (СВО).
Исходя из общего определения ОБПИК-автоматов, определение СВО-автоматов может быть сформулировано следующим образом: слабоинициальный автомат 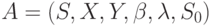 назовем СВО, если
назовем СВО, если
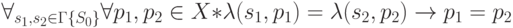 |
( 9.2) |
где  - множество состояний автомата
- множество состояний автомата  , достижимых без состояний множества
, достижимых без состояний множества  .
.
Из этого определения непосредственно следует критерий принадлежности автомата классу СВО.
Лемма 9.2. Слабоинициальный автомат  является СВО-автоматом тогда и только тогда, когда
является СВО-автоматом тогда и только тогда, когда
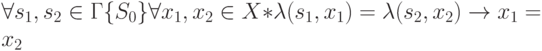 |
( 9.3) |
Отметим существенное различие между (9.1) и (9.2): если в (9.1) используются слова из алфавита  , то в (9.2) фигурируют символы этого алфавита.
, то в (9.2) фигурируют символы этого алфавита.
Пусть 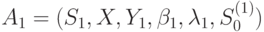 и
и  - два слабоинициальных автомата, тогда автомат
- два слабоинициальных автомата, тогда автомат 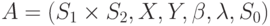 с множеством начальных состояний
с множеством начальных состояний 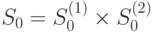 назовем суперпозицией автоматов
назовем суперпозицией автоматов  и
и  , если
, если  .
.
Нетрудно показать справедливость следующего утверждения.
Лемма 9.3. Суперпозиция СВО-автоматов  и
и  является СВО-автоматом.
является СВО-автоматом.
Понятно, что определение суперпозиции (последовательного соединения) может быть распространено на любое конечное число автоматов, но и в этом случае лемма 9.3 остается справедливой. Таким образом, функциональный контроль любого числа последовательно соединенных СВО-автоматов может быть осуществлен по схеме, изображенной на рис.9.1.
Вопросы и упражнения
- Что представляет собой функциональный контроль автомата?
- Опишите принципиальную схему организации такого контроля.
- Опишите схему контроля, основанную на восстановлении входных сигналов.
- Сформулируйте постановку задачи организации контроля с применением ОБПИК-автоматов порядка 1.
- Опишите процедуру преобразования произвольного автомата в ОБПИК-автомат порядка 1 путем выведения контрольных точек.