Эксперименты по контролю функции выходов инициального автомата
Оценки длины кратчайших обходов и характеристических слов
Граф 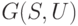 с начальной вершиной
с начальной вершиной  , удовлетворяющий условиям теоремы 6.1, будем называть
, удовлетворяющий условиям теоремы 6.1, будем называть  - правильным или просто правильным. Через
- правильным или просто правильным. Через  обозначим кратчайший обход графа
обозначим кратчайший обход графа 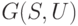 , а через
, а через 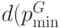 - его длину, т. е. число дуг, входящих в обход.
- его длину, т. е. число дуг, входящих в обход.
По определению обход графа 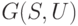 представляет собой путь, содержащий все дуги из
представляет собой путь, содержащий все дуги из  . Отсюда следует нижняя оценка длины кратчайшего обхода:
. Отсюда следует нижняя оценка длины кратчайшего обхода:
 |
( 6.1) |
Возникает вопрос, существуют ли графы, для которых эта оценка достижима, и если да, то как описать такой класс графов. Ответы на эти вопросы даются следующей теоремой.
Теорема 6.2. Для правильного графа 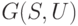 обход длины
обход длины 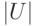 существует тогда и только тогда, когда выполняется одно из следующих условий:
существует тогда и только тогда, когда выполняется одно из следующих условий:
- в каждой вершине графа число исходящих дуг равно числу заходящих;
- в начальной вершине
 графа число исходящих дуг на единицу больше числа заходящих, и существует такая вершина
графа число исходящих дуг на единицу больше числа заходящих, и существует такая вершина  , в которой число исходящих дуг на единицу меньше числа заходящих; в остальных вершинах графа число исходящих дуг равно числу заходящих.
, в которой число исходящих дуг на единицу меньше числа заходящих; в остальных вершинах графа число исходящих дуг равно числу заходящих.
Справедливость этой теоремы следует из известных результатов теории графов [25]. Очевидно, что путь (контур) в графе длины 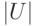 , проходящий через все его дуги и только по одному разу, есть не что иное, как эйлеров путь (контур). Условия сформулированной теоремы являются соответственно условиями существования эйлерова контура и пути.
, проходящий через все его дуги и только по одному разу, есть не что иное, как эйлеров путь (контур). Условия сформулированной теоремы являются соответственно условиями существования эйлерова контура и пути.
Далее обход графа 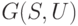 , начинающийся в вершине
, начинающийся в вершине  и заканчивающийся в одной из вершин множества
и заканчивающийся в одной из вершин множества  , будем именовать
, будем именовать 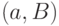 -обходом.
-обходом.
 -обход, т. е. обход в определенном ранее смысле, будем называть
-обход, т. е. обход в определенном ранее смысле, будем называть  -обходом, чтобы отметить его начальную вершину. Если
-обходом, чтобы отметить его начальную вершину. Если  , то
, то 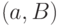 -обход будем называть
-обход будем называть  -обходом.
-обходом.
Для установления верхней оценки длины кратчайших обходов введем несколько определений и докажем ряд вспомогательных утверждений.
Через  обозначим разность между числом заходящих и исходящих дуг вершины
обозначим разность между числом заходящих и исходящих дуг вершины  графа
графа 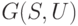 .
.
Определение 6.2. Вершину  графа
графа 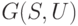 , у которой
, у которой  ), назовем положительной (отрицательной).
), назовем положительной (отрицательной).
Через  обозначим множество всех положительных (отрицательных) вершин графа
обозначим множество всех положительных (отрицательных) вершин графа 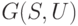 .
.
Определение 6.3. Семейство  элементарных путей назовем компенсирующей системой путей графа
элементарных путей назовем компенсирующей системой путей графа  для
для  -обхода, если:
-обхода, если:
- каждая положительная (отрицательная) вершина
 , отличная от
, отличная от  и
и  , является началом
, является началом  (концом
(концом  ) путей из
) путей из  , где
, где 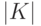 - модуль
- модуль  ;
; - при
 вершина
вершина  является началом
является началом  (концом
(концом 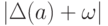 ) путей из
) путей из  , где
, где  , если
, если 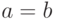 , и
, и 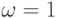 , если
, если 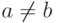 ;
; - если
 ), то вершина
), то вершина  является началом
является началом 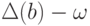 (концом
(концом  ) путей из
) путей из  , где
, где  определяется так же, как в пункте 2.
определяется так же, как в пункте 2.
Сумму длины всех путей из  назовем длиной компенсирующей системы
назовем длиной компенсирующей системы  и обозначим ее через
и обозначим ее через 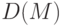 .
.
Через 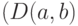 обозначим длину кратчайшего
обозначим длину кратчайшего  -обхода графа
-обхода графа  . Легко убедиться, что для правильных графов компенсирующая система всегда существует.
. Легко убедиться, что для правильных графов компенсирующая система всегда существует.
Теорема 6.3.  , где
, где  - компенсирующая система минимальной длины для
- компенсирующая система минимальной длины для  -обхода графа
-обхода графа 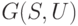 .
.
Доказательство. Каждому пути из  , ведущему из вершины
, ведущему из вершины  в вершину
в вершину  , поставим во взаимно однозначное соответствие дугу, соединяющую те же вершины. Пусть множество этих дуг есть
, поставим во взаимно однозначное соответствие дугу, соединяющую те же вершины. Пусть множество этих дуг есть  . Рассмотрим граф
. Рассмотрим граф 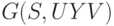 , полученный из
, полученный из 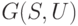 добавлением всех дуг множества
добавлением всех дуг множества  . Легко видеть, что в графе
. Легко видеть, что в графе 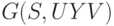 существует эйлеров путь
существует эйлеров путь  , ведущий из вершины
, ведущий из вершины  в вершину
в вершину  (см. теорему параграфа 28 из [25]). Заменив в
(см. теорему параграфа 28 из [25]). Заменив в  каждую дугу
каждую дугу 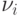 соответствующим ему путем из
соответствующим ему путем из  , получим новый путь
, получим новый путь 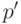 , проходящий только по дугам графа
, проходящий только по дугам графа 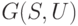 и являющийся его
и являющийся его  -обходом. Из сказанного следует, что
-обходом. Из сказанного следует, что 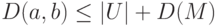 . Неравенство
. Неравенство  вытекает из того, что
вытекает из того, что  - компенсирующая система минимальной длины. Из приведенных неравенств следует справедливость утверждения теоремы.
- компенсирующая система минимальной длины. Из приведенных неравенств следует справедливость утверждения теоремы.
Будем говорить, что граф 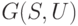 имеет степень
имеет степень  , если из каждой его вершины исходит ровно
, если из каждой его вершины исходит ровно  дуг.
дуг.
Теорема 6.4. Для сильно связного графа 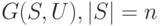 степени
степени  и диаметра
и диаметра  имеет место неравенство
имеет место неравенство
 |
( 6.2) |
Доказательство. Поскольку при 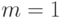 теорема очевидна, то рассмотрим случай
теорема очевидна, то рассмотрим случай  . Число дуг графа
. Число дуг графа  , т. е.
, т. е. 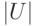 , равно
, равно 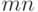 , но тогда в силу теоремы 6.3 достаточно доказать, что существует компенсирующая система путей
, но тогда в силу теоремы 6.3 достаточно доказать, что существует компенсирующая система путей  графа
графа  для
для  -обхода, длина которой не превосходит величины
-обхода, длина которой не превосходит величины  .
.
Пусть 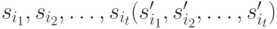 - неупорядоченная последовательность вершин графа
- неупорядоченная последовательность вершин графа 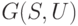 , таких, которые в соответствии с определением 6.3 являются начальными (конечными) вершинами путей компенсирующей системы
, таких, которые в соответствии с определением 6.3 являются начальными (конечными) вершинами путей компенсирующей системы  графа
графа  . Факт существования системы
. Факт существования системы  для сильно связного графа очевиден.
для сильно связного графа очевиден.
Если некоторая вершина является началом (концом)  путей системы
путей системы  , где
, где  , то в последовательности
, то в последовательности 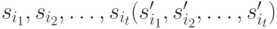 она встречается
она встречается  раз.
раз.
Построение компенсирующей системы путей  будем выполнять в виде пошагового процесса.
будем выполнять в виде пошагового процесса.
1-й шаг. Находим кратчайший путь 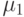 среди путей, ведущих из вершины
среди путей, ведущих из вершины  в вершину
в вершину 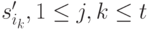 . Путь
. Путь 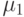 является первым путем компенсирующей системы
является первым путем компенсирующей системы  . Предположим, что
. Предположим, что 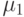 начинается в вершине
начинается в вершине  и заканчивается в вершине
и заканчивается в вершине 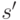 . Вычеркиваем
. Вычеркиваем  и
и 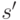 из соответствующих последовательностей вершин, выписанных выше.
из соответствующих последовательностей вершин, выписанных выше.
 -й шаг. Пусть уже построены пути
-й шаг. Пусть уже построены пути 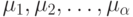 компенсирующей системы
компенсирующей системы  , где
, где  . Тогда последовательность начальных (конечных) вершин путей системы
. Тогда последовательность начальных (конечных) вершин путей системы  содержит на данном шаге
содержит на данном шаге 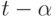 членов. Не теряя общности, можно считать, что такая последовательность начальных (конечных) вершин суть
членов. Не теряя общности, можно считать, что такая последовательность начальных (конечных) вершин суть 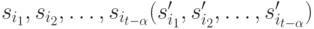 . Находим кратчайший путь
. Находим кратчайший путь  среди путей, ведущих из вершины
среди путей, ведущих из вершины  в вершину
в вершину 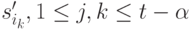 . Пусть
. Пусть  является
является  -м путем компенсирующей системы
-м путем компенсирующей системы  .
.
Построение компенсирующей системы путей  заканчивается, когда из последовательности ее начальных (конечных) вершин будут вычеркнуты все элементы.
Предположим, что по описанному алгоритму построена компенсирующая система путей
заканчивается, когда из последовательности ее начальных (конечных) вершин будут вычеркнуты все элементы.
Предположим, что по описанному алгоритму построена компенсирующая система путей  . Покажем, что при любом
. Покажем, что при любом 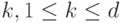 , система эта содержит
, система эта содержит  путей длины, не меньшей
путей длины, не меньшей  , где
, где  .
.
Допустим противное. Пусть  - пути системы
- пути системы  длины, не меньшей
длины, не меньшей  , где
, где 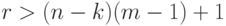 . Поскольку
. Поскольку  сильно связен, то каждая вершина из множества
сильно связен, то каждая вершина из множества  является концом не более чем для
является концом не более чем для 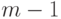 путей из
путей из  . Очевидно, что вершина
. Очевидно, что вершина  может являться концом не более чем для
может являться концом не более чем для  путей системы
путей системы  . Из этого следует, что среди вершин, являющихся конечными для путей
. Из этого следует, что среди вершин, являющихся конечными для путей  из
из  длины, не меньшей
длины, не меньшей  , найдется по крайней мере
, найдется по крайней мере  различных. Тогда, если
различных. Тогда, если  является начальной вершиной некоторого пути
является начальной вершиной некоторого пути  , среди конечных вершин путей
, среди конечных вершин путей 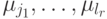 найдется вершина
найдется вершина 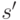 , такая, что длина кратчайшего пути из
, такая, что длина кратчайшего пути из  в
в 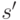 не превышает
не превышает  . Это противоречит нашему предположению.
. Это противоречит нашему предположению.
Обозначим через 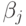 число путей длины
число путей длины  в компенсирующей системе путей
в компенсирующей системе путей  графа
графа 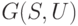 для
для  -обхода. Очевидно, что общая длина всех путей из
-обхода. Очевидно, что общая длина всех путей из  определяется следующим образом:
определяется следующим образом:
![D(M)=\sum_{j=1}^{d}j*\beta_j \le \sum_{k=1}^{d}[(n-k)(m-1)+1]=\frac 12 (m-1)(2n-d-1)d+d](/sites/default/files/tex_cache/deaf9bcee74e4f1b3787fdc0b8f6a15d.png)
Покажем, что оценка (6.2) является достижимой. Рассмотрим граф на рис.6.3.
Из каждой вершины графа выходит  дуг с отметками
дуг с отметками  . Для простоты на этом рисунке кратные дуги заменены одной дугой с кратной отметкой. Легко видеть, что для всех
. Для простоты на этом рисунке кратные дуги заменены одной дугой с кратной отметкой. Легко видеть, что для всех 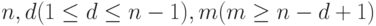 и для всех
и для всех  длина кратчайшего
длина кратчайшего 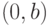 -обхода графа
-обхода графа  точно равна оценке (6.2).
точно равна оценке (6.2).
Теорема 6.5. Пусть 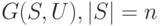 , есть сильно связный граф степени
, есть сильно связный граф степени  , у которого удалена одна дуга, исходящая из вершины
, у которого удалена одна дуга, исходящая из вершины  . Если после удаления этой дуги граф
. Если после удаления этой дуги граф  остался сильно связным и диаметр его равен
остался сильно связным и диаметр его равен  , то для любой вершины
, то для любой вершины  этого графа справедливо неравенство
этого графа справедливо неравенство
 |
( 6.3) |
Доказательство. При 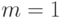 сильно связный граф
сильно связный граф  представляет собой следующую конструкцию: из
представляет собой следующую конструкцию: из  -й вершины дуга ведет в
-й вершины дуга ведет в  -ю для
-ю для  , а из
, а из  -й вершины в первую. Очевидно, что удаление любой дуги из
-й вершины в первую. Очевидно, что удаление любой дуги из  превращает его в граф, не являющийся сильно связным. Поэтому мы покажем справедливость оценки (6.3) при
превращает его в граф, не являющийся сильно связным. Поэтому мы покажем справедливость оценки (6.3) при  .
.
Пусть 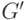 - сильно связный граф, полученный из
- сильно связный граф, полученный из  удалением одной дуги, исходящей из вершины
удалением одной дуги, исходящей из вершины  . Добавим к этому графу петлю в ту же вершину. Полученный в результате новый граф обозначим через
. Добавим к этому графу петлю в ту же вершину. Полученный в результате новый граф обозначим через 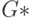 . Построим компенсирующую систему путей
. Построим компенсирующую систему путей  для
для  -обхода графа
-обхода графа 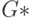 по алгоритму, изложенному при доказательстве теоремы 6.4. Рассуждения, аналогичные приведенным при доказательстве предыдущей теоремы, показывают, что компенсирующая система путей
по алгоритму, изложенному при доказательстве теоремы 6.4. Рассуждения, аналогичные приведенным при доказательстве предыдущей теоремы, показывают, что компенсирующая система путей  для
для  -обхода графа
-обхода графа 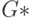 при любом
при любом 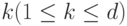 содержит
содержит  путей длины, не меньшей
путей длины, не меньшей  , причем
, причем 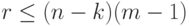 . Отсюда следует, что общая длина
. Отсюда следует, что общая длина 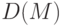 путей компенсирующей системы
путей компенсирующей системы  графа
графа  удовлетворяет неравенству
удовлетворяет неравенству
![D(M) \le \sum_{k=1}^{d}[(n-k)(m-1)]\frac 12 (m-1)(2n-d-1)d=](/sites/default/files/tex_cache/16c16cd70683151db3446ba24145a92b.png)
Тогда длина  -обхода графа
-обхода графа 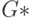 не превосходит величины
не превосходит величины 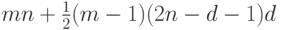 . Нетрудно убедиться, что среди
. Нетрудно убедиться, что среди  -обходов графа
-обходов графа 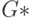 , удовлетворяющих оценке (6.3), есть такой, у которого добавленная фиктивная петля является последней в этом обходе, т. е. обход имеет следующую структуру:
, удовлетворяющих оценке (6.3), есть такой, у которого добавленная фиктивная петля является последней в этом обходе, т. е. обход имеет следующую структуру: 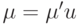 , где
, где  - дуга фиктивной петли в вершине
- дуга фиктивной петли в вершине  . Отсюда следует, что путь
. Отсюда следует, что путь 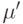 является
является  -обходом графа
-обходом графа 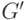 , а длина его не превосходит величины
, а длина его не превосходит величины  .
.
Покажем, что оценка (6.3) является достижимой. С этой целью вновь обратимся к графу, изображенному на рис.6.3. Непосредственным подсчетом легко убедиться, что для всех 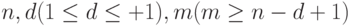 и
и  , если удалить одну дугу (произвольным образом) рассматриваемого графа, длина
, если удалить одну дугу (произвольным образом) рассматриваемого графа, длина  -обхода в точности равна оценке (6.3).
-обхода в точности равна оценке (6.3).
Рассмотрим теперь обход графов, не являющихся сильно связными.
Пусть 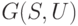 -
-  правильный граф, число слоев которого есть
правильный граф, число слоев которого есть  . Обозначим через
. Обозначим через  подграф графа
подграф графа  , соответствующий его
, соответствующий его  -му слою. Легко видеть, что
-му слою. Легко видеть, что 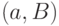 -обход графа
-обход графа  существует тогда и только тогда, когда
существует тогда и только тогда, когда 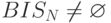 и
и  есть
есть  -правильный граф.
-правильный граф.
Пусть 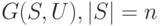 , есть граф степени
, есть граф степени  , являющийся
, являющийся  -правильным. Предположим, что
-правильным. Предположим, что  - слои графа
- слои графа  , которые занумерованы в соответствии с процедурой нумерации, описанной в разделе 6.1. Условимся считать, что
, которые занумерованы в соответствии с процедурой нумерации, описанной в разделе 6.1. Условимся считать, что  , а диаметр
, а диаметр  есть
есть  . Пусть
. Пусть  - дуга, ведущая из вершины
- дуга, ведущая из вершины  в вершину
в вершину  . Через
. Через 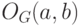 обозначим
обозначим  -обход графа
-обход графа  . Очевидно, что
. Очевидно, что 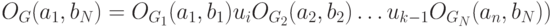 . Из этого, а также теорем 6.3 и 6.5 вытекает справедливость следующего утверждения.
. Из этого, а также теорем 6.3 и 6.5 вытекает справедливость следующего утверждения.
Теорема 6.6.

где  - компенсирующая система путей минимальной длины графа
- компенсирующая система путей минимальной длины графа  для
для 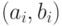 -обхода.
-обхода.
Следствие 1. Длина кратчайшего  -обхода (следовательно, и
-обхода (следовательно, и  -обхода) графа
-обхода) графа  не превосходит величины
не превосходит величины
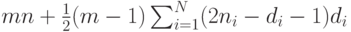 |
( 6.4) |
Доказательство. В силу теоремы 6.4 достаточно доказать, что для каждого из графов  , у которого удалена дуга, ведущая из вершины
, у которого удалена дуга, ведущая из вершины 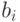 в вершину
в вершину  графа
графа  , существует компенсирующая система путей
, существует компенсирующая система путей  для
для 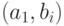 -обхода, а для графа
-обхода, а для графа  - система
- система  для
для  -обхода, для которых справедливо неравенство
-обхода, для которых справедливо неравенство

Методом, аналогичным использованному в доказательстве теоремы 6.5, можно показать, что длина компенсирующей системы путей графа  для
для  -обхода не превышает величины
-обхода не превышает величины
 |
( 6.5) |
Длина компенсирующей системы путей  для
для 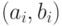 -обхода графа
-обхода графа 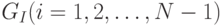 с одной удаленной дугой, ведущей из
с одной удаленной дугой, ведущей из 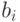 в
в  , в силу оценки (3.3) удовлетворяет неравенству
, в силу оценки (3.3) удовлетворяет неравенству

Отсюда следует, что
![D(a_1, a_N) \le mn+ \frac 12 \sum_{i=1}^{N_1}[(m-1)(2n_i-d_i-1)d_i-1]+\\
+\frac 12 (m-1)(2n_N-d_N-1)d_N+(N-1)=mn+\frac 12 (m-1) \sum_{i=1}^{N}(2n_i-d_i-1)d_i](/sites/default/files/tex_cache/c8f2e43db97705c9418008b05b6cae69.png)
Замечание. На основании (6.5) получаем, что длина  -обхода
-обхода  -вершинного сильно связного графа степени
-вершинного сильно связного графа степени  удовлетворяет неравенству
удовлетворяет неравенству
 |
( 6.6) |
Известно, что диаметр  -вершинного графа не превосходит величины
-вершинного графа не превосходит величины  . Заменяя в (3.6)
. Заменяя в (3.6)  на
на  , получаем
, получаем
 |
( 6.7) |
Таким образом, оценка (6.7), установленная в работе [36] , следует из оценки (6.6).
Следствие 2. Если в графе 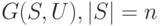 , степени
, степени 
 -обход существует, то длина кратчайшего
-обход существует, то длина кратчайшего  -обхода не превосходит величины
-обхода не превосходит величины
 |
( 6.8) |
Это следствие непосредственно вытекает из теорем 6.5 и 6.6.
Легко показать, что оценки (6.4) и (6.8) достижимы. Для этого достаточно построить граф  , слой
, слой 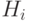 которого есть подграф, изображенный на рис.6.3. В каждом из этих подграфов произведем следующие изменения: дугу
которого есть подграф, изображенный на рис.6.3. В каждом из этих подграфов произведем следующие изменения: дугу  -го подграфа
-го подграфа 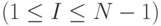 , исходящую из вершины с номером
, исходящую из вершины с номером 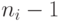 с отметкой
с отметкой  , заменим дугой с той же отметкой и исходящей из той же вершины, но заходящей в вершину с номером 0
, заменим дугой с той же отметкой и исходящей из той же вершины, но заходящей в вершину с номером 0  -го подграфа. Непосредственным подсчетом можно убедиться, что оценки (6.4) и (6.8) для графа
-го подграфа. Непосредственным подсчетом можно убедиться, что оценки (6.4) и (6.8) для графа  достижимы.
достижимы.
Из полученных результатов следует, что точная нижняя оценка длины кратчайших характеристических слов автомата есть оценка (6.1), а точные верхние оценки следующие: для сильно связного автомата - (6,2) и (6.7), для остальных - (6.8).
Вопросы и упражнения
- Приведите постановку задачи контроля функции выходов инициального автомата.
- Приведите критерий существования обхода графа и его доказательство.
- Дайте определение характеристического слова автомата.
- Каков критерий существования характеристического слова автомата?
- Каковы условия существования обхода графа минимально возможной длины?
- Что представляет собой компенсирующая система путей графа ?
- Приведите верхние оценки различных типов обходов. Какие из этих оценок являются достижимыми?

