НОУ ИНТУИТ | Теория экспериментов с конечными автоматами. Лекция 5: Преобразования автоматов в автоматы без потери информации

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 17.02.2011 | Доступ: свободный | Студентов: 367 / 35 | Оценка: 5.00 / 5.00 | Длительность: 25:24:00

ISBN: 978-5-9963-0268-0

Тема: Алгоритмы и дискретные структуры

Специальности: Математик

|

Вам нравится? Нравится 3 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Построение множества дуг, упомянутого выше, будет проводиться в виде пошагового процесса. Одновременно с этим будет проводиться построение "каркаса" разбиения $\Pi$ множества .

Вначале произведем следующие преобразования над матрицей переходов автомата :

удаляем из все дуги, имеющие в качестве выходных символы, не содержащиеся в выражении ;
если элемент матрицы содержит две дуги с различными входными, но одинаковыми выходными символами, то одну из этих дуг, выбираемую произвольно, включаем в множество и удаляем ее из матрицы .

Отметим при этом, что удаленная и оставленная в матрице [A] дуги должны находиться в разных классах разбиения $\Pi$ (это и есть информация о "каркасе" разбиения $\Pi$ ).

Описанный процесс продолжается далее до тех пор, пока элемент 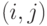(i, j) не будет содержать ни одной пары дуг с указанным выше свойством.

Легко видеть, что удаленные в соответствии с пунктом (a) дуги заведомо таковы, что путь в графе автомата , соответствующий любому слову из заданного регулярного множества , не может содержать их.

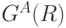Удаление из матрицы [A] дуг согласно пункту (b) соответствует удалению выделенных дуг множества из проверочного графа G^A(R) . Очевидно, что пара дуг графа автомата с различными входными, но одинаковыми выходными символами является выделенной дугой проверочного графа G^A(R) .

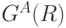Преобразованную описанным способом матрицу переходов будем, как и ранее, обозначать [A] .

Описываемые ниже преобразования будут производиться над матрицами [A]^k при $k=1,2, \dots$ , получаемыми из $[A]^{k-1}$ путем умножения ее слева на преобразованную матрицу переходов [A] .

Итак, рассмотрим матрицу переходов [A}^k . Произведем над ней следующие преобразования:

Если элемент матрицы содержит два пути, которым соответствуют различные входные, но одинаковые выходные слова, то каждой дуге, входящей в состав этих путей, присваиваем вес, равный числу вхождений этой дуги во все пути матрицы переходов . Дугу с максимальным весом включаем в множество и удаляем из все пути, содержащие эту дугу. Из матрицы переходов дуга с максимальным весом также удаляется.

Этот процесс продолжается далее до тех пор, пока элемент 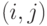не будет содержать ни одной пары путей с описанным выше свойством.
Среди всех путей матрицы находим пути, соответствующие входным (выходным) словам, которые не могут являться отрезками никаких слов из заданного множества . Указанные пути удаляются из матрицы переходов .

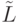Как уже было отмечено, удаление дуг множества из графа автомата соответствует удалению дуг некоторого множества $\tilde L$ из проверочного графа G^A(R) .

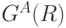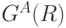Пусть выполнены описанные выше преобразования над матрицей переходов [A] и при этом получено множество дуг графа автомата . Удаляем из G^A(R) множество 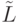$\tilde L$ дуг, соответствующее множеству , и проверяем выполнение условий теоремы 5.2. Если условия выполняются, то преобразования матриц переходов на этом завершаются. Для построения искомого разбиения $\Pi$ можно далее воспользоваться уже описанным методом. Если же условия теоремы 5.2 не выполняются, то вычисляем следующую степень матрицы переходов [A] и выполняем над ней описанные преобразования. Затем вновь следует проверка условий теоремы 5.2 и процесс продолжается аналогичным образом.

Из описанных преобразований следует, что выполнение условий теоремы 5.2 будет достигнуто за конечное число шагов.

Продемонстрируем предложенный метод на примере, который уже был рассмотрен выше. Итак, пусть автомат задан табл. 5.1, а множество задается выражением R=a(ba*)*a .

Исходная матрица переходов имеет следующий вид:

$[A]= \left [ \begin {matrix} 1 \xrightarrow {1,c}1& 1\xrightarrow {2,c}2& 1\xrightarrow {1,a}3 & 0\\ & 1\xrightarrow {0,a}2&&\\ 2\xrightarrow {1,b}1& 2\xrightarrow {2,c}2& 2\xrightarrow {3,c}3& 2\xrightarrow {0,a}4\\ 0& 3\xrightarrow {0,b}2& 3\xrightarrow {2,d}3& 3\xrightarrow {1,a}4\\ &3\xrightarrow {0,f}2 &&\\ 0& 4\xrightarrow {1,b}2& 4\xrightarrow {0,a}3& 4\xrightarrow {2,f}4\\ &&4\xrightarrow {3,d}3 & \end {matrix} \right ]$

Преобразованная матрица после удаления дуг из элементов (1,1), (2,2), (2,3), (3,2), (3,3), (4,3), (4,4) на основании пункта (a) и дуги $1 \xrightarrow {2,a}2$ из элемента (1,2) на основании пункта (b) примет вид

$[A]= \left [ \begin {matrix} 0& 1\xrightarrow {0,a}2& 1\xrightarrow {1,a}3&0\\ 2\xrightarrow {1,b}&0&0&2\xrightarrow {0.a}\\ 0& 3\xrightarrow {0,b}3& 0& 3\xrightarrow {1,a}4\\ 0&4\xrightarrow {1,b}2&4\xrightarrow {0,a}3&0 \end {matrix} \right ]$

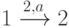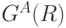Дуга $1\xrightarrow {2,a}2$ включается в множество , причем она должна быть в разных классах разбиения $\Pi$ с дугой $1\xrightarrow {0,a}2$ . Указанной паре дуг в проверочном графе G^A(R) соответствует выделенная дуга $\{1,1\}==\stackrel{0,2,a}{\Longrightarrow} \{2,2\}$ .

После удаления выделенной дуги из 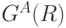G^A(R) этот граф не удовлетворяет условиям теоремы 5.2, поэтому вычислим матрицу переходов [A]^2 :

$[A]^2= \left [ \begin {matrix} 1\xrightarrow {0,a}2\xrightarrow {1,b}1& 1\xrightarrow {1,a}3\xrightarrow {0,b}2&0& 1\xrightarrow {0,a}2\xrightarrow {0,a}4\\ &&&1\xrightarrow {1,a}3\xrightarrow {1,c}4\\ 0&2\xrightarrow {1,b}1\xrightarrow {0,a}2& 2\xrightarrow {1,b}1\xrightarrow {1,a}3&0\\ &2\xrightarrow {0,a}4\xrightarrow {1,b}2& 2\xrightarrow {0,a}4\xrightarrow {0,a}3&\\ 3\xrightarrow {0,b}2\xrightarrow {1,b}1& 3\xrightarrow {1,a}4\xrightarrow {1,b}2& 3\xrightarrow {1,a}4 \xrightarrow {0,a}3& 3\xrightarrow {0,b}2\xrightarrow {0,a}4\\ 4\xrightarrow {1,b}2\xrightarrow {1,b}1& 4\xrightarrow {0,a}3\xrightarrow {0,b}2& 0& 4\xrightarrow {1,b}2\xrightarrow {0,a}4\\ &&&4\xrightarrow {0,a}3\xrightarrow 1,a}4 \end {matrix} \right ]$

Удалим дуги из элементов (3,1) и (4,1) на основании пункте 2, так как слово 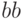не принадлежит событию a(ba*)*a . Пути элемента (1,4) удовлетворяют условию, сформулированному в пункте 1. Максимальный вес (равный 5) среди всех дуг, входящих в состав этих путей, имеет дуга $2\xrightarrow {0,a}4$ . Включаем эту дугу в множество и удаляем из [A]^2 все пути, содержащие ее. После этого преобразования матрица примет следующий вид:

$[A]^2= \left [ \begin {matrix} 1\xrightarrow {0,a}2\xrightarrow {1,b}1 & 1\xrightarrow {1,a}3\xrightarrow {0,b}2 & 0 & 1\xrightarrow {1,a}3\xrightarrow {1,c}4\\ 0 & 2\xrightarrow {1,b}1\xrightarrow {0,a}2 & 2\xrightarrow {1,b}1\xrightarrow {1,a}3 & 0\\ 0 & 3\xrightarrow {1,a}4\xrightarrow {1,b}2 & 3\xrightarrow {1,a}4\xrightarrow {0,a}3 & 0\\ 0 & 4\xrightarrow {0,a}3\xrightarrow {0,b}2 & 0 & 4\xrightarrow {0,a}3\xrightarrow {1a}4 \end {matrix} \right ]$

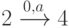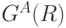Удаление дуги $2 \xrightarrow {0,a}4$ из графа автомата соответствует удалению выделенных дуг $\{2,3\} ==\stackrel{0,1,a}{\Longrightarrow} \{4,4\}; \{1,2\} ==\stackrel{0,2,a}{\Longrightarrow} \{2,4\}; \{1,2\} ==\stackrel{1,0,a}{\Longrightarrow} \{3,4\}$ в проверочном графе G^A(R) , а также дуги $\{1,2\} \xrightarrow {0,0,a} \{2,4\}$ .

Легко проверить, что после удаления названных дуг граф 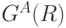G^A(R) удовлетворяет условиям теоремы 5.2.

Таким образом, изменив выходные сигналы при переходах $1\xrightarrow {2,a} 2$ и $2 \xrightarrow {0,a} 4$ в графе автомата , например, следующим образом: $1 \xrightarrow {2, a1} 2, 2\xrightarrow {0,a1} 4$ , мы удовлетворяем требованию, чтобы дуги $1 \xrightarrow {2, a1} 2, 1 \xrightarrow {0,a} 2$ , принадлежали разным классам разбиения.

Поскольку число полученных классов разбиения равно 2, то для кодирования символов классов достаточно одной двоичной переменной. Это означает, что у автомата достаточно вывести одну дополнительную выходную контрольную точку. Таблицей автомата с контрольными точками в силу сказанного выше является табл. 5.3.

Таблица 5.3.
s\x	0	1	2	3
1	2, a 0	3, a 0	2, a 1	1, c 0
2	4, a 1	1, b 0	2, c 0	3, c 0
3	2, b 0	4, a 0	3, d 0	2, f 0
4	3, a 0	2, b 0	4, f 0	3, d 0

Итак, мы получим еще один вариант автомата с контрольными точками, являющегося -БПИ-автоматом, где событие представлено выражением R=a(ba*)*a .

Вопросы и упражнения

Дайте определение автомата БПИ на заданном регулярном множестве его входных слов.
Сформулируйте основную идею метода решения задачи преобразования автомата в автомат БПИ на регулярном множестве слов.
Сформулируйте две вспомогательных задачи, к решению которых сводится проблема исследуемого преобразования автомата в автомат БПИ.
Опишите кратко основные идеи методов решения двух вспомогательных задач.

Дальше >>

Авторизоваться

Теория экспериментов с конечными автоматами

Преобразования автоматов в автоматы без потери информации

Вопросы и упражнения

Вопросы и ответы