Обобщенные автоматы без потери информации
Нетрудно убедиться, что упомянутое в пункте 2 алгоритма множество есть 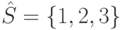 . Установочной последовательностью для рассматриваемого автомата с множеством допустимых начальных состояний
. Установочной последовательностью для рассматриваемого автомата с множеством допустимых начальных состояний 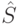 является, например, слово длиной два
является, например, слово длиной два 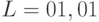 . Пользуясь таблицей 3.1, по действительной реакции автомата на слово
. Пользуясь таблицей 3.1, по действительной реакции автомата на слово  находим состояния
находим состояния 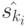 , упомянутые в пункте 3 алгоритма.
, упомянутые в пункте 3 алгоритма.
| Состояние автомата | ВХОДНАЯ ПОСЛЕДОВАТЕЛЬ-НОСТЬ | Реакция автомата | Заключительное состояние |
|---|---|---|---|
| 1 | 01,01 | 00,00 | 1 |
| 2 | 01,01 | 10,10 | 1 |
| 3 | 01,01 | 10,00 | 1 |
Если 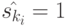 , то ему соответствуют пары (1;10,00,00), (1;10,00,01), (1;10,01,00), (1;10,01,01), …, (1;11,01,00) и проекцией по 1-му входному каналу неизвестного входного слова является 1,0,0. При
, то ему соответствуют пары (1;10,00,00), (1;10,00,01), (1;10,01,00), (1;10,01,01), …, (1;11,01,00) и проекцией по 1-му входному каналу неизвестного входного слова является 1,0,0. При 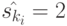 искомая проекция есть 1,0,1 и, например, при
искомая проекция есть 1,0,1 и, например, при 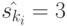 проекция равна 1,1,1.
проекция равна 1,1,1.
Хотя теорема 3.1 позволила обосновать метод восстановления искомой проекции неизвестного входного слова, однако ответить с ее помощью на вопрос, является ли конкретный автомат ОБПИ-автоматом, сложно из-за отсутствия эффективного способа проверки условий теоремы. Ввиду этого ниже сформулируем еще одно необходимое и достаточное условие принадлежности автомата классу ОБПИ, но в других по сравнению с теоремой 3.1 терминах, допускающее простую проверку.
С этой целью по аналогии с [74] введем понятие проверочного графа автомата. Условимся считать, что автомат задан с помощью конечного ориентированного графа. Будем говорить, что дуга 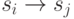 графа автомата
графа автомата  , где
, где 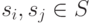 , имеет пометку
, имеет пометку  , если
, если  .
.
Аналогичное определение сформулируем и для случая, когда выходной символ 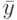 наблюдается не по всем, а только по
наблюдается не по всем, а только по  выделенным каналам с номерами
выделенным каналам с номерами 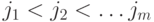 : дуга
: дуга 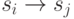 имеет пометку
имеет пометку  , если
, если

Понятно, что две вершины графа могут связываться несколькими дугами с разными пометками.
Пусть  - множество всех состояний автомата
- множество всех состояний автомата  , достижимых из множества допустимых начальных состояний
, достижимых из множества допустимых начальных состояний  путями любой длины.
путями любой длины.
По графу автомата  построим другой ориентированный конечный граф
построим другой ориентированный конечный граф  следующим образом.
следующим образом.
- Вершинами
 являются все возможные неупорядоченные пары
являются все возможные неупорядоченные пары 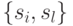 , где
, где  .
. - Из вершины
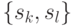 в вершину
в вершину 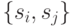 проводится дуга с пометкой
проводится дуга с пометкой  , если
, если 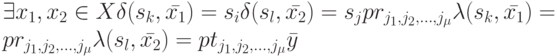
В графе  две вершины могут быть связаны несколькими дугами с разными пометками.
две вершины могут быть связаны несколькими дугами с разными пометками.
Пусть неизвестное входное слово необходимо восстановить по каналам с номерами 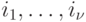 , где
, где 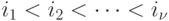 .
.
Дугу 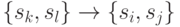 с пометкой
с пометкой  назовем выделенной, если
назовем выделенной, если
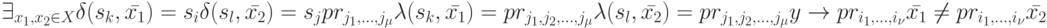
Из графа  удалим все вершины вида
удалим все вершины вида 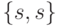 вместе с инцидентными им дугами, если последние, в свою очередь, инцидентны только вершинам такого же вида, а также изолированные вершины. Полученный в результате такого удаления ориентированный конечный граф назовем проверочным графом автомата
вместе с инцидентными им дугами, если последние, в свою очередь, инцидентны только вершинам такого же вида, а также изолированные вершины. Полученный в результате такого удаления ориентированный конечный граф назовем проверочным графом автомата  и обозначим его
и обозначим его  .
.
Теорема 3.2. Автомат  является ОБПИ-автоматом тогда и только тогда, когда все пути в проверочном графе
является ОБПИ-автоматом тогда и только тогда, когда все пути в проверочном графе  , ведущие в вершины вида
, ведущие в вершины вида 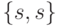 , не содержат выделенных дуг.
, не содержат выделенных дуг.
Необходимость. Пусть  есть ОБПИ-автомат, но в
есть ОБПИ-автомат, но в  существует путь с выделенной дугой
существует путь с выделенной дугой 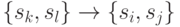 , ведущий в вершину вида
, ведущий в вершину вида 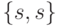 . Предположим, что
. Предположим, что 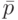 и
и 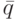 - два таких входных слова, что
- два таких входных слова, что 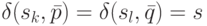 , и они соответствуют пути по графу в
, и они соответствуют пути по графу в  , начинающемуся с упомянутой выделенной дуги. Последнее означает, что
, начинающемуся с упомянутой выделенной дуги. Последнее означает, что
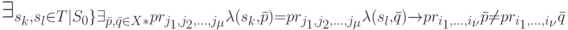
Из сравнения этого высказывания с (3.1) вытекает, что  не может быть ОБПИ-автоматом, а это противоречит исходной посылке.
не может быть ОБПИ-автоматом, а это противоречит исходной посылке.
Достаточность. Докажем ее методом от противного. Пусть  не является ОБПИ-автоматом. Покажем тогда, что в графе
не является ОБПИ-автоматом. Покажем тогда, что в графе  существует путь, ведущий в вершину вида
существует путь, ведущий в вершину вида 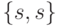 , содержащий выделенную дугу. Поскольку
, содержащий выделенную дугу. Поскольку  не есть ОБПИ-автомат, то
не есть ОБПИ-автомат, то
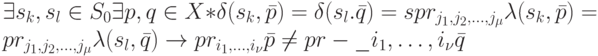
Пусть 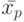 и
и 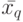 - первые слева символы в словах
- первые слева символы в словах 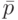 и
и 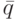 , проекции которых по каналам
, проекции которых по каналам 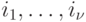 различны. Пусть при подаче этих символов автомат
различны. Пусть при подаче этих символов автомат  осуществляет переходы из состояний
осуществляет переходы из состояний  в состояния
в состояния 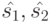 соответственно. Отсюда следует, что в графе
соответственно. Отсюда следует, что в графе  существует выделенная дуга, соединяющая вершины
существует выделенная дуга, соединяющая вершины 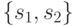 и
и 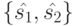 . Это означает существование в графе
. Это означает существование в графе  пути из
пути из 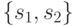 в
в 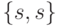 , первая дуга которого выделенная. Этим завершается доказательство достаточности условий теоремы.
, первая дуга которого выделенная. Этим завершается доказательство достаточности условий теоремы.
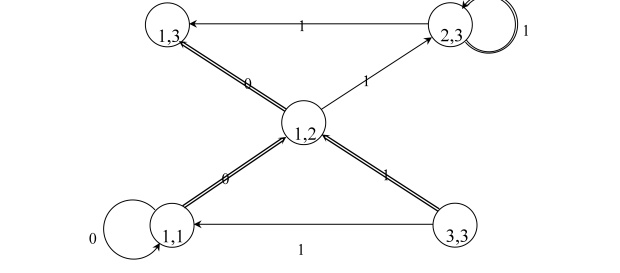
В качестве примера на рис.3.2 изображен проверочный граф для автомата, представленного на рис.3.1, в предположении, что 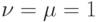 . На рисунке двойные стрелки соответствуют выделенным дугам, над каждой дугой стоит соответствующая ей пометка. В этом проверочном графе все возможные пути, заканчивающиеся в вершинах вида
. На рисунке двойные стрелки соответствуют выделенным дугам, над каждой дугой стоит соответствующая ей пометка. В этом проверочном графе все возможные пути, заканчивающиеся в вершинах вида 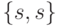 , могут начинаться только в вершинах
, могут начинаться только в вершинах 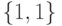 либо
либо 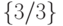 , при этом конечной вершиной в любом из этих путей является вершина
, при этом конечной вершиной в любом из этих путей является вершина 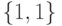 . Из рис.3.2 видно, что ни один из этих путей не содержит выделенных дуг, следовательно, рассматриваемый автомат относится к классу ОБПИ-автоматов.
. Из рис.3.2 видно, что ни один из этих путей не содержит выделенных дуг, следовательно, рассматриваемый автомат относится к классу ОБПИ-автоматов.
Если задан автомат  с
с  входными и
входными и  выходными каналами, то возникает вопрос: для каких подмножеств входных и выходных каналов он является ОБПИ-автоматом? Очевидно, что
выходными каналами, то возникает вопрос: для каких подмножеств входных и выходных каналов он является ОБПИ-автоматом? Очевидно, что  может не быть БПИ-автоматом в классическом смысле, но в то же время быть ОБПИ-автоматом, если восстановление входных сигналов производится по некоторому подмножеству входных каналов.
может не быть БПИ-автоматом в классическом смысле, но в то же время быть ОБПИ-автоматом, если восстановление входных сигналов производится по некоторому подмножеству входных каналов.
При отыскании всех возможных подмножеств входных и выходных каналов, для которых заданный автомат  является ОБПИ-автоматом, в первую очередь представляет интерес случай, когда подмножество входных каналов - максимальное, а подмножество выходных каналов - минимальное по мощности. Далее такой автомат будем называть оптимальным. Это соответствует ситуации, когда при минимальных затратах, определяемых объемом наблюдаемой информации на выходах, удается однозначно восстановить максимальный объем информации, поступившей на вход автомата.
является ОБПИ-автоматом, в первую очередь представляет интерес случай, когда подмножество входных каналов - максимальное, а подмножество выходных каналов - минимальное по мощности. Далее такой автомат будем называть оптимальным. Это соответствует ситуации, когда при минимальных затратах, определяемых объемом наблюдаемой информации на выходах, удается однозначно восстановить максимальный объем информации, поступившей на вход автомата.
Опишем способ, позволяющий получить ответ на сформулированный выше вопрос. Условимся далее через 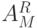 обозначать автомат, у которого выходные символы наблюдаются по каналам с номерами из множества
обозначать автомат, у которого выходные символы наблюдаются по каналам с номерами из множества  , а восстановление сигналов ведется по каналам с номерами из множества
, а восстановление сигналов ведется по каналам с номерами из множества  .
.
По графу автомата  построим его проверочный граф
построим его проверочный граф  при
при 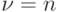 и
и 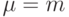 , т. е. предполагая, что реакция
, т. е. предполагая, что реакция  наблюдается по всем его выходным каналам, а восстановление неизвестного входного слова также ведется по всем каналам. Используя
наблюдается по всем его выходным каналам, а восстановление неизвестного входного слова также ведется по всем каналам. Используя  , найдем в нем все пути, ведущие в вершины вида
, найдем в нем все пути, ведущие в вершины вида 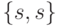 , и образуем на этой основе множество
, и образуем на этой основе множество 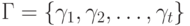 всех входящих в эти пути выделенных дуг. Если
всех входящих в эти пути выделенных дуг. Если  , то по теореме 3.2 автомат
, то по теореме 3.2 автомат  есть ОБПИ-автомат, и при
есть ОБПИ-автомат, и при 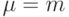 он будет, очевидно, таковым для любого
он будет, очевидно, таковым для любого  , где
, где 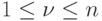 . Если
. Если  , то для каждого
, то для каждого 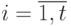 построим множество
построим множество 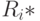 целых чисел, представляющих собой номера входных каналов, на которых на дуге
целых чисел, представляющих собой номера входных каналов, на которых на дуге  происходит потеря информации. Последнее означает, что если реакция автомата
происходит потеря информации. Последнее означает, что если реакция автомата  соответствует отметке дуги
соответствует отметке дуги  , то в каналах с номерами из множества
, то в каналах с номерами из множества  сигналы могут иметь значения как 0, так и 1. Используя множество
сигналы могут иметь значения как 0, так и 1. Используя множество 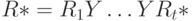 , построим
, построим 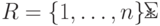 . Из способа построения следует, что, во-первых,
. Из способа построения следует, что, во-первых,  содержит все те номера входных каналов, по каждому из которых и по их совокупности рассматриваемый автомат
содержит все те номера входных каналов, по каждому из которых и по их совокупности рассматриваемый автомат  является ОБПИ-автоматом, и, во-вторых,
является ОБПИ-автоматом, и, во-вторых,  - максимальный по мощности, сохраняющий свойство ОБПИ.
- максимальный по мощности, сохраняющий свойство ОБПИ.
Далее через 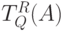 обозначим проверочный граф автомата
обозначим проверочный граф автомата  , предполагая, что наблюдение реакций ведется по каналам с номерами из множества
, предполагая, что наблюдение реакций ведется по каналам с номерами из множества  , а восстановление неизвестного входного слова - по каналам с номерами из множества
, а восстановление неизвестного входного слова - по каналам с номерами из множества  .
.
Пусть 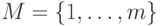 . Для каждого
. Для каждого 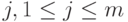 , построим проверочный граф
, построим проверочный граф 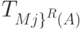 . Нетрудно сообразить, что дуги графа
. Нетрудно сообразить, что дуги графа 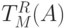 одновременно являются и дугами графа
одновременно являются и дугами графа 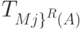 , но в последнем, кроме того, могут появиться и новые. Если последний упомянутый граф удовлетворяет условиям теоремы 3.2, то, очевидно,
, но в последнем, кроме того, могут появиться и новые. Если последний упомянутый граф удовлетворяет условиям теоремы 3.2, то, очевидно,  -й выходной канал избыточен в том смысле, что отказ от наблюдения реакции по нему не повлияет на возможности восстановления неизвестного входного слова по каналам из множества
-й выходной канал избыточен в том смысле, что отказ от наблюдения реакции по нему не повлияет на возможности восстановления неизвестного входного слова по каналам из множества  . Пусть
. Пусть 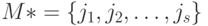 - множество номеров всех избыточных выходных каналов автомата
- множество номеров всех избыточных выходных каналов автомата  . Если
. Если 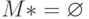 , то построенный на 1-м этапе автомат
, то построенный на 1-м этапе автомат 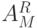 - искомый. При
- искомый. При  рассмотрим все возможные сочетания пар каналов из множества
рассмотрим все возможные сочетания пар каналов из множества 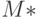 , число которых равно
, число которых равно  . Для каждой из упомянутых пар каналов
. Для каждой из упомянутых пар каналов 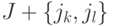 построим проверочный граф
построим проверочный граф 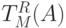 и проверим для него выполнение условий теоремы 3.2. Если ни один из таких графов не удовлетворяет условиям этой теоремы, то автоматы
и проверим для него выполнение условий теоремы 3.2. Если ни один из таких графов не удовлетворяет условиям этой теоремы, то автоматы 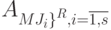 , - искомые оптимальные автоматы. В противном случае формируем все возможные сочетания
, - искомые оптимальные автоматы. В противном случае формируем все возможные сочетания 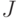 троек номеров из множества
троек номеров из множества 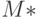 и ищем среди проверочных графов
и ищем среди проверочных графов 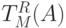 такие, которые удовлетворяют условиям теоремы 3.2. Указанный процесс продолжается до того момента, когда на очередном этапе все графы вида
такие, которые удовлетворяют условиям теоремы 3.2. Указанный процесс продолжается до того момента, когда на очередном этапе все графы вида 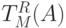 , где
, где 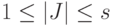 , не удовлетворяют условиям теоремы 3.2. Тогда автоматы
, не удовлетворяют условиям теоремы 3.2. Тогда автоматы  , построенные на предыдущем этапе и являющиеся ОБПИ-автоматами, - искомые оптимальные.
, построенные на предыдущем этапе и являющиеся ОБПИ-автоматами, - искомые оптимальные.
Отметим, что для поиска всех оптимальных ОБПИ-автоматов в худшем случае может потребоваться построение 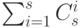 различных проверочных графов, где
различных проверочных графов, где  - число избыточных выходных каналов автомата
- число избыточных выходных каналов автомата  .
.
Вопросы и упражнения
- Дайте определение пары состояний с потерей информации.
- Сформулируйте определение обобщенного автомата без потери информации.
- Приведите критерий принадлежности автомата классу автоматов ОБПИ в терминах СПИ-состояний.
- Опишите процедуру распознавания проекции неизвестного входного слова, поданного на ОБПИ-автомат.
- Опишите процедуру построения проверочного графа автомата.
- Приведите критерий принадлежности автомата классу ОБПИ-автоматов в терминах проверочного графа.
- Дайте определение оптимального ОБПИ-автомата.
- ОБПИ-автомат задан графом на рис.3.1. Пусть для наблюдения реакции выделен 1-й выходной канал автомата (он соответствует левому символу входной пары), а проекция неизвестного входного слова должна быть восстановлена по первому входному каналу. Пусть множество допустимых начальных состояний автомата есть
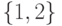 . На этот автомат подано неизвестное входное слово длины 2, а по первому выходному каналу наблюдалась реакция 0,1. Требуется восстановить проекцию по первому каналу неизвестного входного слова.
. На этот автомат подано неизвестное входное слово длины 2, а по первому выходному каналу наблюдалась реакция 0,1. Требуется восстановить проекцию по первому каналу неизвестного входного слова.