Синтез экспериментов методами динамического программирования
Синтез установочной последовательности
Решение задачи синтеза УП, минимальной по весу, будет состоять из двух этапов, первый из которых заключается в построении по таблице переходов-выходов автомата графа, называемого графом установки автомата (ГУА), а второй - в поиске на нем минимальной УП.
ГУА - это ориентированный граф, каждая вершина которого отмечается  -группой
-группой  -множеств. Отметка вершины используется в качестве ее имени. Если
-множеств. Отметка вершины используется в качестве ее имени. Если  -группа, которой отмечена некоторая вершина
-группа, которой отмечена некоторая вершина  ГУА, под воздействием входного сигнала
ГУА, под воздействием входного сигнала 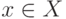 переходит в
переходит в  -группу, которой отмечена вершина
-группу, которой отмечена вершина 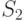 , то в ГУА из
, то в ГУА из  в
в 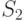 проводится дуга, на которой ставится входной сигнал
проводится дуга, на которой ставится входной сигнал  . Правила преобразования одной
. Правила преобразования одной  -группы в другую под воздействием входного сигнала
-группы в другую под воздействием входного сигнала  остаются такими же, как они определены выше.
остаются такими же, как они определены выше.
Построение ГУА осуществляется рекурсивно и по существу совпадает с процессом построения установочного дерева из [18].
Вначале в число вершин графа включается вершина  , где
, где  - множество допустимых начальных состояний. Вершину
- множество допустимых начальных состояний. Вершину  поместим на вертикальную прямую и назовем ее линией 1-го уровня. Далее строим все
поместим на вертикальную прямую и назовем ее линией 1-го уровня. Далее строим все  -группы, в которые переходит
-группы, в которые переходит  -группа
-группа  под воздействием всех символов входного алфавита
под воздействием всех символов входного алфавита  , включаем их в число вершин ГУА и помещаем на линию уровня с номером 2. Из вершины
, включаем их в число вершин ГУА и помещаем на линию уровня с номером 2. Из вершины  в вершины второго уровня проводим по упомянутому правилу дуги, помеченные соответствующими входными символами. Процесс построения ГУА продолжается далее аналогичным образом (как и в случае установочного дерева). При этом если на очередном шаге построения появилась вершина, соответствующая однородной
в вершины второго уровня проводим по упомянутому правилу дуги, помеченные соответствующими входными символами. Процесс построения ГУА продолжается далее аналогичным образом (как и в случае установочного дерева). При этом если на очередном шаге построения появилась вершина, соответствующая однородной  -группе, то такая вершина считается листом, т. е. при продолжении процесса построения ГУА из нее не будет больше исходить никаких дуг.
-группе, то такая вершина считается листом, т. е. при продолжении процесса построения ГУА из нее не будет больше исходить никаких дуг.
У каждой вершины 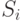 ГУА установим флажок (на рисунке он, как и ранее, изображается в виде квадрата); в него записывается число, равное сумме весов входных символов последовательности, которая ведет из
ГУА установим флажок (на рисунке он, как и ранее, изображается в виде квадрата); в него записывается число, равное сумме весов входных символов последовательности, которая ведет из  в
в 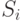 . Теперь введем некоторые дополнительные правила, используемые при построении ГУА:
. Теперь введем некоторые дополнительные правила, используемые при построении ГУА:
- если на очередной линии уровня появилась вершина
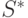 , а на одной из линий уровня с меньшим номером имеется вершина
, а на одной из линий уровня с меньшим номером имеется вершина 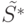 , помеченная такой же
, помеченная такой же  -группой, что и
-группой, что и  , причем число во флажке у вершины
, причем число во флажке у вершины 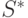 больше, чем во флажке у вершины
больше, чем во флажке у вершины 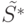 , то вершина
, то вершина  становится листом, а если она является непосредственным преемником вершины с такой же
становится листом, а если она является непосредственным преемником вершины с такой же  -группой, то она удаляется из ГУА;
-группой, то она удаляется из ГУА; - если значение флажка у некоторой вершины
 , появившейся на очередном шаге построения ГУА, больше, чем у какой-либо вершины, помеченной однородной
, появившейся на очередном шаге построения ГУА, больше, чем у какой-либо вершины, помеченной однородной  -группой, находящейся на предыдущих уровнях, то вершина
-группой, находящейся на предыдущих уровнях, то вершина  удаляется из ГУА.
удаляется из ГУА.
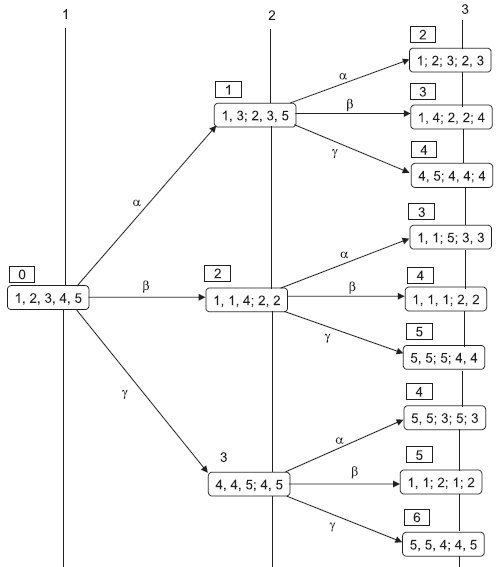
Понятно, что описанный процесс построения ГУА всегда завершается за конечное число шагов. Проиллюстрируем построение ГУА для автомата, заданного табл. 1.1, считая, что 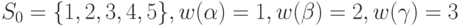 . Обратимся к рис.2.2, на котором изображен соответствующий ГУА. На третьем шаге построения ГУА, как это видно из рисунка, возникло 9 вершин, среди которых вершины
. Обратимся к рис.2.2, на котором изображен соответствующий ГУА. На третьем шаге построения ГУА, как это видно из рисунка, возникло 9 вершин, среди которых вершины  не являются однородными, а остальные - однородные. Последние именно по этой причине становятся листьями. Заметим, что вершина
не являются однородными, а остальные - однородные. Последние именно по этой причине становятся листьями. Заметим, что вершина  среди однородных имеет минимальное значение флажка, равное 3. Теперь перейдем к четвертому шагу. Так, самая верхняя вершина 3-го уровня
среди однородных имеет минимальное значение флажка, равное 3. Теперь перейдем к четвертому шагу. Так, самая верхняя вершина 3-го уровня 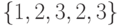 под воздействием сигнала
под воздействием сигнала  переходит в вершину, помеченную такой же
переходит в вершину, помеченную такой же  -группой. Поскольку она является непосредственным преемником вершины с такой же
-группой. Поскольку она является непосредственным преемником вершины с такой же  -группой, по правилу 1 она удаляется из ГУА. Аналогичная ситуация имеет место для вершины
-группой, по правилу 1 она удаляется из ГУА. Аналогичная ситуация имеет место для вершины 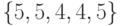 (самая нижняя на 3-м уровне) при построении вершины 4-го уровня, в которую она переходит под воздействием входного символа
(самая нижняя на 3-м уровне) при построении вершины 4-го уровня, в которую она переходит под воздействием входного символа  .
.
Легко убедиться, что при построении остальных вершин 4-го уровня в их флажках будут стоять числа, большие 3, но тогда по правилу 2 они все должны быть удалены из ГУА. Таким образом, граф ГУА содержит только три уровня.
Из самого способа построения ГУА вытекает, что последовательность входных символов, соответствующая пути по ГУА из вершины  в одну из однородных вершин, будет являться УП для заданного автомата.
в одну из однородных вершин, будет являться УП для заданного автомата.
Покажем теперь, что задача синтеза минимальной по весу УП всегда может быть сведена к задаче выбора наискорейшего пути, как это было и в случае СП.
Роль опорных прямых здесь выполняют линии уровня, а сам ГУА можно интерпретировать как сеть дорог, удовлетворяющую необходимым требованиям для упомянутой задачи, поскольку в нем, во-первых, отсутствуют петли, а, во-вторых, все дуги направлены от вершин  -го уровня к вершинам
-го уровня к вершинам  -го уровня, т. е. отсутствуют "обратные" дуги.
-го уровня, т. е. отсутствуют "обратные" дуги.
Понятно, что если положить время движения по дуге равным весу входного символа, которым она помечена, то задача синтеза УП минимального веса сводится к задаче о выборе наискорейшего пути из вершины  в однородные вершины ГУА. Отсюда вытекает, что для решения рассматриваемой нами задачи можно применить метод динамического программирования.
в однородные вершины ГУА. Отсюда вытекает, что для решения рассматриваемой нами задачи можно применить метод динамического программирования.
Вместе с тем заметим, что ГУА представляет собой дерево, а в дереве, как известно, если между некоторой парой его вершин путь существует, то он единственен. Следовательно, применительно к ГУА задача поиска пути из вершины  в некоторую однородную вершину превращается в тривиальную задачу. Более того, для каждой однородной вершины в ее флажке записано число, равное времени, затрачиваемому на путь в нее из
в некоторую однородную вершину превращается в тривиальную задачу. Более того, для каждой однородной вершины в ее флажке записано число, равное времени, затрачиваемому на путь в нее из  .
.
Таким образом, располагая этими данными для нахождения оптимального пути, достаточно найти ту из однородных вершин, у которой число во флажке минимально. Очевидно, что искомой УП минимального веса будет входная последовательность, соответствующая пути по ГУА из вершины  в однородную вершину с минимальным числом во флажке.
в однородную вершину с минимальным числом во флажке.
Так, в ГУА на рис.2.2 имеется 5 однородных вершин, среди которых минимальное число во флажке, равное 3, имеет вершина 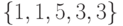 . Поскольку пути по ГУА из вершины
. Поскольку пути по ГУА из вершины  в нее соответствует входная последовательность
в нее соответствует входная последовательность 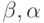 , то она и является минимальной по весу УП.
, то она и является минимальной по весу УП.
Синтез диагностической последовательности
Решение задачи синтеза ДП, минимальной по весу, по аналогии с изложенным выше, будет состоять из двух этапов. На первом из них по таблице переходов-выходов заданного автомата строится граф, называемый графом диагностики автомата (ГДА), а на втором - производится поиск на построенном графе минимальной ДП.
ГДА представляет собой ориентированный граф, множество вершин которого и способ проведения дуг между ними полностью совпадает с тем, как это было определено для ГУА. По аналогии с предыдущим разделом у каждой вершины ГДА устанавливается флажок, значение которого определяется точно так же, как и в случае ГУА.
Вершины ГДА, которые отмечены  -группами, содержащими кратные (только простые)
-группами, содержащими кратные (только простые)  -множества, будем называть кратными (простыми).
-множества, будем называть кратными (простыми).
Построение ГДА аналогично построению диагностического дерева автомата, описанному в [18], но при этом вводятся несколько иные, чем в [18], правила, по которым вершина  (по терминологии [18] - ветвь)
(по терминологии [18] - ветвь)  -го уровня становится листом.
-го уровня становится листом.
Вершина 
 -го уровня ГДА становится листом, если:
-го уровня ГДА становится листом, если:
-
 является простой вершиной;
является простой вершиной; -
 является кратной вершиной;
является кратной вершиной; - в уровнях ГДА, предшествующих
 -му, имеется вершина
-му, имеется вершина 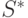 , помеченная такой же
, помеченная такой же  -группой, что и вершина
-группой, что и вершина  , но у вершины
, но у вершины  значение флажка больше, чем у
значение флажка больше, чем у 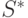 ;
; - в уровнях, предшествующих
 -му, имеется простая вершина, значение флажка которой меньше, чем значение флажка вершины
-му, имеется простая вершина, значение флажка которой меньше, чем значение флажка вершины  .
.
Легко показать, что введенные правила обрыва ветвей гарантируют построение ГДА за конечное число шагов.
Проиллюстрируем предложенный способ построения ГДА на примере автомата, таблица переходов-выходов которого отличается от табл. 1.1 только содержимым левой верхней клетки: под воздействием сигнала  автомат из состояния 1 переходит опять в состояние 1, но при этом его выходной сигнал равен 1, а не 0, как в табл. 1.1. Предполагается, что множество допустимых начальных состояний есть
автомат из состояния 1 переходит опять в состояние 1, но при этом его выходной сигнал равен 1, а не 0, как в табл. 1.1. Предполагается, что множество допустимых начальных состояний есть 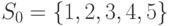 , а
, а 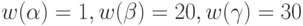 .
.
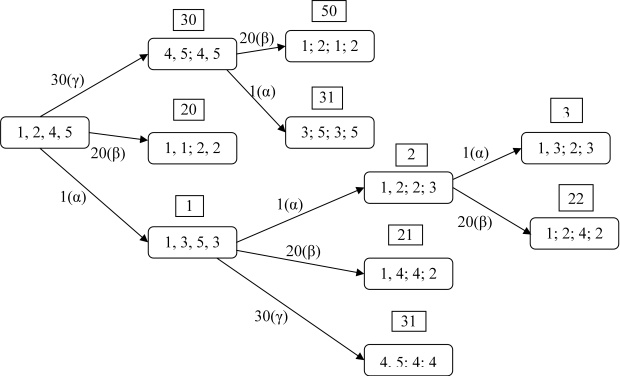
На рис.2.3 изображен ГДА для этого автомата. Проиллюстрируем теперь, как работают введенные правила завершения. Так, на третьем шаге построения ГДА появляется вершина  со значением флажка, равным 60, в которую ведет дуга, помеченная входным символом
со значением флажка, равным 60, в которую ведет дуга, помеченная входным символом  , из вершины
, из вершины  второго уровня со значением флажка, равным 30. Тогда, в силу пункта 3 правил завершения, вершина
второго уровня со значением флажка, равным 30. Тогда, в силу пункта 3 правил завершения, вершина  3-го уровня удаляется. Далее: среди вершин 4-го уровня, появившихся в процессе построения ГДА, имеется простая вершина
3-го уровня удаляется. Далее: среди вершин 4-го уровня, появившихся в процессе построения ГДА, имеется простая вершина 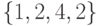 со значением флажка, равным 22. Легко убедиться, что на 5-м шаге построения ГДА у всех появляющихся вершин значения флажков будут больше 22, но тогда в силу пункта 4 правил завершения все эти вершины должны быть удалены из ГДА. Таким образом, ГДА для нашего примера будет содержать только четыре уровня. Отметим также, что вершина
со значением флажка, равным 22. Легко убедиться, что на 5-м шаге построения ГДА у всех появляющихся вершин значения флажков будут больше 22, но тогда в силу пункта 4 правил завершения все эти вершины должны быть удалены из ГДА. Таким образом, ГДА для нашего примера будет содержать только четыре уровня. Отметим также, что вершина  второго уровня является оконечной в силу пункта 2 правил завершения, вершины
второго уровня является оконечной в силу пункта 2 правил завершения, вершины 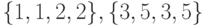 второго уровня и вершина
второго уровня и вершина 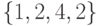 третьего уровня становятся оконечными в силу пункта 1 правил завершения.
третьего уровня становятся оконечными в силу пункта 1 правил завершения.
Из способа построения ГДА вытекает, что последовательность входных символов, соответствующая пути по ГДА из вершины  в одну из простых вершин, будет являться ДП для заданного автомата.
в одну из простых вершин, будет являться ДП для заданного автомата.
Отметим, что поиск упомянутых путей представляет собой тривиальную задачу, поскольку ГДА является деревом, и потому каждый такой путь единственен. Понятно, что построение ДП с минимальным весом сводится к следующему. Среди всех простых вершин ГДА отыскивается вершина  с минимальным значением флажка. Затем в этом графе находится единственный путь из
с минимальным значением флажка. Затем в этом графе находится единственный путь из  в
в  , которому соответствует определенная последовательность входных символов. Построенная таким образом входная последовательность и является искомой ДП, минимальной по весу.
, которому соответствует определенная последовательность входных символов. Построенная таким образом входная последовательность и является искомой ДП, минимальной по весу.
Так, в ГДА на рис.2.3имеется 3 простых вершины, из которых у вершины 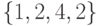 четвертого уровня значение флажка минимально и равно 22. Поскольку пути по ГДА из вершины
четвертого уровня значение флажка минимально и равно 22. Поскольку пути по ГДА из вершины  в эту вершину соответствует входная последовательность
в эту вершину соответствует входная последовательность 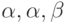 , то она и является минимальной по весу ДП. Заметим, кстати, что минимальной ДП в классическом смысле для этого примера будет являться входная последовательность
, то она и является минимальной по весу ДП. Заметим, кстати, что минимальной ДП в классическом смысле для этого примера будет являться входная последовательность  , соответствующая пути по ГДА из вершины
, соответствующая пути по ГДА из вершины  в вершину
в вершину  третьего уровня.
третьего уровня.
Вопросы и упражнения
- Сформулируйте метод построения графа синхронизации (установки, диагностики) автомата.
- Сформулируйте процедуру построения минимальной по весу СП с использованием ГСА.
- Какие линии в ГСА выступают в роли опорных прямых при построении искомой СП методом динамического программирования?
- Для автомата из упражнения 9 к лекции 1 построить ГСА и по этому графу методом динамического программирования найти минимальную по весу СП в предположении, что
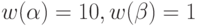 и
и 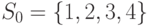 .
. - Для того же автомата построить ГУА и по этому графу методом динамического программирования найти минимальную по весу УП в предположении, что
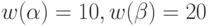 и
и 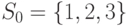 .
. - Для автомата из предыдущего упражнения при тех же предположениях о весах входных символов и множестве
 начальных состояний построить ГДА и по этому графу найти минимальную по весу ДП.
начальных состояний построить ГДА и по этому графу найти минимальную по весу ДП.