НОУ ИНТУИТ | Прикладная статистика. Лекция 6: Оценивание

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 09.11.2009 | Доступ: свободный | Студентов: 3994 / 952 | Оценка: 4.66 / 4.45 | Длительность: 54:13:00

Темы: Математика, Экономика

Специальности: Экономист

|

Вам нравится? Нравится 61 студенту

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Для получения асимптотического распределения статистики 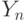Y_n вида (2) можно применить метод линеаризации к асимптотически нормальному вектору выборочных моментов $(M_{n1},M_{n2},...,M_{nq})$ и функции из формулы (2).

В силу многомерной центральной предельной теоремы (см. "Теоретическая база прикладной статистики" ) указанная асимптотическая нормальность имеет место, если, например,

$M|x_i|^{2q+1}<+\infty.$

Это условие выполнено, в частности, для результатов измерений, распределения которых сосредоточены на ограниченных сверху и снизу интервалах.

При реализации намеченного плана для применения формулы (4) необходимо использовать асимптотические дисперсии и ковариации выборочных моментов, т.е. величины, обозначенные в формуле (4) как $c_{rs}$ . Эти величины имеют вид [ [ 4.23 ] , с.388]:

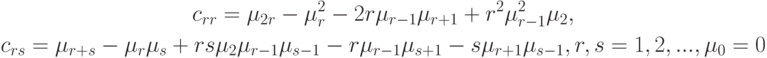$\begin{gathered} c_{rr}=\mu_{2r}-\mu_r^2-2r\mu_{r-1}\mu_{r+1}+r^2\mu_{r-1}^2\mu_2, \\ c_{rs}=\mu_{r+s}-\mu_r\mu_s+rs\mu_2\mu_{r-1}\mu_{s-1}-r\mu_{r-1}\mu_{s+1}-s\mu_{r+1}\mu_{s-1},r,s=1,2,...,\mu_0=0 \end{gathered}$

( 5)

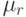Здесь $\mu_r$ - теоретический центральный момент порядка , т.е.

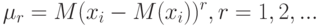
$\mu_r=M(x_i-M(x_i))^r,r=1,2,...$

Таким образом, для получения асимптотического распределения случайной величины 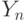Y_n вида (2) достаточно знать теоретические центральные моменты результатов наблюдений и вид функции . Отметим, что асимптотическим смещением оценок в рассматриваемом случае можно пренебречь, поскольку его вклад в средний квадрат ошибки статистической оценки - бесконечно малая величина более высокого порядка по сравнению с асимптотической дисперсией.

Однако моменты неизвестны. Их приходится оценивать. В соответствии с теоремами о наследовании сходимости для нахождения асимптотического распределения функции от выборочных моментов можно воспользоваться не теоретическими моментами, а их состоятельными оценками. Эти оценки можно получить разными способами. Можно непосредственно применить формулы (5), заменив теоретические моменты выборочными. Можно выразить моменты через параметры рассматриваемого распределения. Можно применять более сложные процедуры, например, на основе непараметрических устойчивых (робастных) оценок моментов типа урезанных средних Пуанкаре и др. (в первой в России книге по общей теории устойчивости [ [ 1.15 ] ] проблематика робастных оценок рассмотрена в "Основы вероятностно-статистических методов описания неопределенностей" ).

Для оценивания параметров гамма-распределения воспользуемся известной формулой [ [ 6.6 ] , с.42], согласно которой для случайной величины , имеющей гамма-распределение с параметрами формы , масштаба b=1 и сдвига c=0 ,

$M(X^m)=\frac{\Gamma(a+m)}{\Gamma(a)}=a(a+1)...(a+m-1), m=1,2,...$

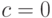( 6)

Следовательно, M(X) = a, M(X^2) = a(a+1), D(X) = M(X^2) - (M(X))^2 = a(a+1) - a^2 = a . Найдем третий центральный момент M(X - M(X))^3 . Справедливо равенство

M(X - M(X))^3 = M(X^3) - 3 M(X^2) M(X) + 3 M(X) (M(X))^2 - (M(X))^3.

Из равенства (6) вытекает, что

M(X - M(X))^3 = a(a+1)(a+2) - 3 a (a+1) a + 3 a a^2 - a^3 = 2a.

Если - случайная величина, имеющая гамма-распределение с произвольными параметрами формы , масштаба и сдвига , то Y = bX + c . Следовательно,

M(Y) = ab+c, D(Y) = ab^2, M(Y - M(Y))^3 = 2 a b^3.

Пример 2. Оценивание методом моментов параметров гамма-распределения в случае трех неизвестных параметров (строка 7 табл.6.1).

В соответствии с проведенными выше рассуждениями для оценивания трех параметров достаточно использовать три выборочных момента - выборочное среднее арифметическое

$\overline{x}=\frac{x_1+x_2+...+x_n}{n},$

выборочную дисперсию

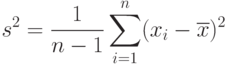
$s^2=\frac{1}{n-1}\sum_{i=1}^n(x_i-\overline{x})^2$

и выборочный третий центральный момент

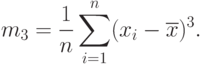
$m_3=\frac{1}{n}\sum_{i=1}^n(x_i-\overline{x})^3.$

Приравнивая теоретические моменты, выраженные через параметры распределения, и выборочные моменты, получаем систему уравнений метода моментов:

$ab+c=\overline{x},ab^2=s^2,2ab^3=m_3.$

Решая эту систему, находим оценки метода моментов. Подставляя второе уравнение в третье, получаем оценку метода моментов для параметра сдвига: 2s^2b=m_3,b*=\frac12\frac{m_3}{s^2}.

Подставляя эту оценку во второе уравнение, находим оценку метода моментов для параметра формы:

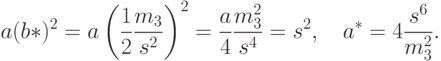
$a(b*)^2=a\left(\frac12\frac{m_3}{s^2}\right)^2=\frac{a}{4}\frac{m_3^2}{s^4}=s^2,\quad a^*=4\frac{s^6}{m_3^2}.$

Наконец, из первого уравнения находим оценку для параметра сдвига:

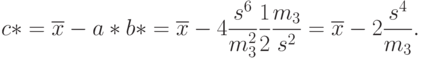
$c*=\overline{x}-a*b*=\overline{x}-4\frac{s^6}{m_3^2}\frac12\frac{m_3}{s^2}=\overline{x}-2\frac{s^4}{m_3}.$

Для реальных данных [ [ 6.6 ] ], приведенных выше в табл.6.2, выборочное среднее арифметическое $\overline{x}=57,88$ , выборочная дисперсия s^2=663,00 , выборочный третий центральный момент m_3=14927,91 . Согласно только что полученным формулам оценки метода моментов таковы: a*=5,23; b*=11,26, c*=-1,01 .

Оценки параметров гамма-распределения, полученные методом моментов, являются функциями от выборочных моментов. В соответствии со сказанным выше они являются асимптотически нормальными случайными величинами. Их распределения аппроксимируются нормальными распределениями, математические ожидания которых равны соответствующим параметрам, а дисперсии находятся с помощью формулы (4) с учетом формул (5) и (6). В табл.6.3 приведены оценки метода моментов и их асимптотические дисперсии при различных вариантах сочетания известных и неизвестных параметров гамма-распределения.

Таблица 6.3. Оценки метода моментов и их асимптотические дисперсии
№ п/п	Описание вероятностной модели			Оцениваемый параметр	Вид оценки	Асимптотическая дисперсия оценки
№ п/п				Оцениваемый параметр	Вид оценки	Асимптотическая дисперсия оценки
1	-	-	+		$\frac{(\overline{x})^2}{s^2}$	$\frac{2a(a+1)}{n}$
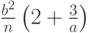2	-	-	+		$\frac{s^2}{\overline{x}}$	$\frac{b^2}{n}\left(2+\frac{3}{a}\right)$
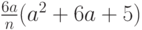3	-	-	-		$4\frac{s^6}{m_3^2}$	$\frac{6a}{n}(a^2+6a+5)$
4	-	-	-		$\frac12\frac{m_3}{s^2}$	$\frac{b^2}{2an}(6a^2+25a+24)$
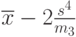5	-	-	-		$\overline{x}-2\frac{s^4}{m_3}$	$\frac{ab^2}{n}(3a^2+13a+10)$
6	+	-	-		$\frac{s}{\sqrt{a}}$	$\frac{b}{2n}(a+3)$
7	+	-	-		$\overline{x}-s\sqrt{a}$	$\frac{ab^2}{2n}(a+1)$
8	-	+	-		$\frac{s^2}{b^2}$	$\frac{2a}{n}(a+3)$
9	-	+	-		$\overline{x}-\frac{s^2}{b}$	$\frac{ab^2}{n}(2a+3)$
10	+	+	-		$\overline{x}-ab$	$\frac{ab^2}{n}$

Примечание. При описании вероятностной модели известные статистику параметры отмечены плюсами, оцениваемые - минусами.

Все оценки метода моментов, приведенные в табл.6.3, включены в государственный стандарт [ [ 6.6 ] ]. Они охватывают все постановки задач оценивания параметров гамма-распределения (см. табл.6.1) , кроме тех, когда неизвестен только один параметр - или . Для этих исключительных случаев в [ [ 6.6 ] ] разработаны специальные методы оценивания.

Поскольку асимптотическое распределение оценок метода моментов известно, то не представляет труда формулировка правил проверки статистических гипотез относительно значений параметров распределений, а также построение доверительных границ для параметров. Например, в вероятностной модели, когда все три параметра неизвестны, в соответствии с третьей строкой таблицы 3 нижняя доверительная граница для параметра а, соответствующая доверительной вероятности $\gamma=0,95$ , в асимптотике имеет вид

$a_H=a*-1,96 \left\{ \frac{6a*}{n}([a*]^2+6a*+5) \right\}^{\frac12},$

а верхняя доверительная граница для той же доверительной вероятности:

$a_B=a*+1,96 \left\{ \frac{6a*}{n}([a*]^2+6a*+5) \right\}^{\frac12},$

где 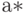- оценка метода моментов параметра формы (табл.6.3).

Дальше >>

Авторизоваться

Прикладная статистика

Оценивание

Вопросы и ответы