НОУ ИНТУИТ | Прикладная статистика. Лекция 6: Оценивание

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 09.11.2009 | Доступ: свободный | Студентов: 4083 / 1035 | Оценка: 4.66 / 4.45 | Длительность: 54:13:00

Темы: Математика, Экономика

Специальности: Экономист

|

Вам нравится? Нравится 61 студенту

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Метод моментов является универсальным. Однако получаемые с его помощью оценки лишь в редких случаях обладают оптимальными свойствами. Поэтому в прикладной статистике применяют и другие виды оценок.

В работах, предназначенных для первоначального знакомства с математической статистикой, обычно рассматривают оценки максимального правдоподобия (сокращенно ОМП):

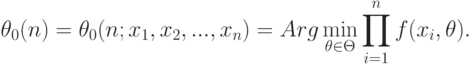$\theta_0(n)=\theta_0(n;x_1,x_2,...,x_n)=Arg\min\limits_{\theta\in\Theta}\prod_{i=1}^nf(x_i,\theta).$

( 7)

Таким образом, сначала строится плотность распределения вероятностей, соответствующая выборке. Поскольку элементы выборки независимы, то эта плотность представляется в виде произведения плотностей для отдельных элементов выборки. Совместная плотность рассматривается в точке, соответствующей наблюденным значениям. Это выражение как функция от параметра (при заданных элементах выборки) называется функцией правдоподобия. Затем тем или иным способом ищется значение параметра, при котором значение совместной плотности максимально. Это и есть оценка максимального правдоподобия.

Хорошо известно, что оценки максимального правдоподобия входят в класс наилучших асимптотически нормальных оценок (определение дано ниже). Однако при конечных объемах выборки в ряде задач ОМП недопустимы, так как они хуже (дисперсия и средний квадрат ошибки больше), чем другие оценки, в частности, несмещенные [ [ 6.13 ] ]. Именно поэтому в ГОСТ 11.010-81 для оценивания параметров отрицательного биномиального распределения используются несмещенные оценки, а не ОМП [ [ 6.5 ] ]. Из сказанного следует, что априорно предпочитать ОМП другим видам оценок можно - если можно - лишь на этапе изучения асимптотического поведения оценок.

В отдельных случаях ОМП находятся явно, в виде конкретных формул, пригодных для вычисления.

Пример 3. Найдем ОМП для выборки из нормального распределения, каждый элемент которой имеет плотность

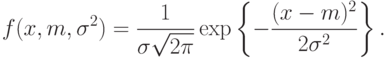
$f(x,m,\sigma^2)=\frac{1}{\sigma\sqrt{2\pi}}\exp\left\{-\frac{(x-m)^2}{2\sigma^2}\right\}.$

Таким образом, надо оценить двумерный параметр 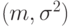$(m, \sigma^2)$ .

Произведение плотностей вероятностей для элементов выборки, т.е. функция правдоподобия, имеет вид

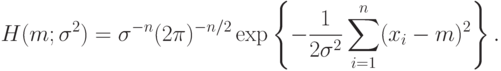$H(m;\sigma^2)=\sigma^{-n}(2\pi)^{-n/2} \exp\left\{-\frac{1}{2\sigma^2}\sum_{i=1}^n(x_i-m)^2\right\}.$

( 8)

Требуется решить задачу оптимизации

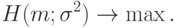
$H(m;\sigma^2)\rightarrow\max.$

Как и во многих иных случаях, задача оптимизации проще решается, если прологарифмировать функцию правдоподобия, т.е. перейти к функции

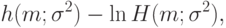
$h(m;\sigma^2)-\ln H(m;\sigma^2),$

называемой логарифмической функцией правдоподобия. Для выборки из нормального распределения

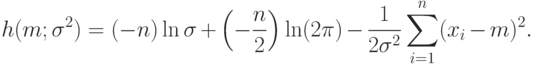$h(m;\sigma^2)=(-n)\ln\sigma+\left(-\frac{n}{2}\right)\ln(2\pi)-\frac{1}{2\sigma^2}\sum_{i=1}^n(x_i-m)^2.$

( 9)

Необходимым условием максимума является равенство 0 частных производных от логарифмической функции правдоподобия по параметрам, т.е.

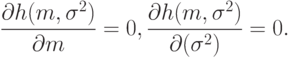$\frac{\partial h(m,\sigma^2)}{\partial m}=0,\frac{\partial h(m,\sigma^2)}{\partial(\sigma^2)}=0.$

( 10)

Система (10) называется системой уравнений максимального правдоподобия. В общем случае число уравнений равно числу неизвестных параметров, а каждое из уравнений выписывается путем приравнивания 0 частной производной логарифмической функции правдоподобия по тому или иному параметру.

При дифференцировании по первые два слагаемых в правой части формулы (9) обращаются в 0, а последнее слагаемое дает уравнение

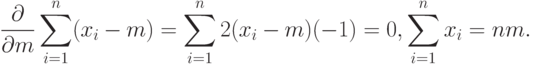
$\frac{\partial}{\partial m}\sum_{i=1}^n(x_i-m)= \sum_{i=1}^n 2(x_i-m)(-1)=0,\sum_{i=1}^n x_i=nm.$

Следовательно, оценкой максимального правдоподобия параметра m является выборочное среднее арифметическое,

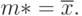
$m*=\overline{x}.$

Для нахождения оценки дисперсии необходимо решить уравнение

$\frac{\partial}{\partial(\sigma^2)}h(m;\sigma^2)= \frac{\partial}{\partial(\sigma^2)}(-n)\ln\sqrt{(\sigma^2)}- \frac{\partial}{\partial(\sigma^2)}\frac{1}{2\sigma^2} \sum_{i=1}^n(x_i-m)^2=0.$

Легко видеть, что

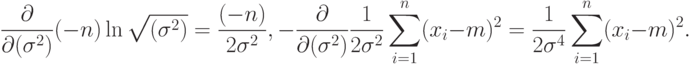
$\frac{\partial}{\partial(\sigma^2)}(-n)\ln\sqrt{(\sigma^2)}=\frac{(-n)}{2\sigma^2}, -\frac{\partial}{\partial(\sigma^2)}\frac{1}{2\sigma^2}\sum_{i=1}^n(x_i-m)^2= \frac{1}{2\sigma^4}\sum_{i=1}^n(x_i-m)^2.$

Следовательно, оценкой 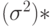$(\sigma^2)*$ максимального правдоподобия для дисперсии $\sigma^2$ с учетом найденной ранее оценки для параметра является выборочная дисперсия,

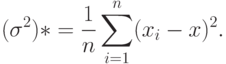
$(\sigma^2)*=\frac{1}{n}\sum_{i=1}^n(x_i-\overlina{x})^2.$

Итак, система уравнений максимального правдоподобия решена аналитически, ОМП для математического ожидания и дисперсии нормального распределения - это выборочное среднее арифметическое и выборочная дисперсия. Отметим, что последняя оценка является смещенной.

Отметим, что в условиях примера 3 оценки метода максимального правдоподобия совпадают с оценками метода моментов. Причем вид оценок метода моментов очевиден и не требует проведения каких-либо рассуждений.

В большинстве случаев аналитических решений не существует, для нахождения ОМП необходимо применять численные методы. Так обстоит дело, например, с выборками из гамма-распределения или распределения Вейбулла-Гнеденко. Во многих работах каким-либо итерационным методом решают систему уравнений максимального правдоподобия ([ [ 6.24 ] ] и др.) или впрямую максимизируют функцию правдоподобия типа (8) (см. [ [ 6.12 ] ] и др.).

Однако применение численных методов порождает многочисленные проблемы. Сходимость итерационных методов требует обоснования. В ряде примеров функция правдоподобия имеет много локальных максимумов, а потому естественные итерационные процедуры не сходятся [ [ 6.7 ] ]. Для данных ВНИИ железнодорожного транспорта по усталостным испытаниям стали уравнение максимального правдоподобия имеет 11 корней [ [ 6.1 ] ]. Какой из одиннадцати использовать в качестве оценки параметра?

Как следствие осознания указанных трудностей, стали появляться работы по доказательству сходимости алгоритмов нахождения оценок максимального правдоподобия для конкретных вероятностных моделей и конкретных алгоритмов. Примером является статья [ [ 6.23 ] ].

Однако теоретическое доказательство сходимости итерационного алгоритма - это еще не всё. Возникает вопрос об обоснованном выборе момента прекращения вычислений в связи с достижением требуемой точности. В большинстве случаев он не решен.

Но и это не все. Точность вычислений необходимо увязывать с объемом выборки - чем он больше, тем точнее надо находить оценки параметров, в противном случае нельзя говорить о состоятельности метода оценивания. Более того, при увеличении объема выборки необходимо увеличивать и количество используемых в компьютере разрядов, переходить от одинарной точности расчетов к двойной и далее - опять-таки ради достижения состоятельности оценок.

Таким образом, при отсутствии явных формул для оценок максимального правдоподобия нахождение ОМП натыкается на ряд проблем вычислительного характера. Специалисты по математической статистике позволяют себе игнорировать все эти проблемы, рассуждая об ОМП в теоретическом плане. Однако прикладная статистика не может их игнорировать. Отмеченные проблемы ставят под вопрос целесообразность практического использования ОМП.

Нет необходимости абсолютизировать ОМП. Кроме них, существуют другие виды оценок, обладающих хорошими статистическими свойствами. Примером являются одношаговые оценки (ОШ-оценки).

В прикладной статистике разработано много видов оценок. Упомянем квантильные оценки. Они основаны на идее, аналогичной методу моментов, но только вместо выборочных и теоретических моментов приравниваются выборочные и теоретические квантили. Другая группа оценок базируется на идее минимизации расстояния (показателя различия) между эмпирическими данными и элементом параметрического семейства. В простейшем случае минимизируется евклидово расстояние между эмпирическими и теоретическими гистограммами, а точнее, векторами, составленными из высот столбиков гистограмм.

Дальше >>

Авторизоваться

Прикладная статистика

Оценивание

Вопросы и ответы