НОУ ИНТУИТ | Прикладная статистика. Лекция 6: Оценивание

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 09.11.2009 | Доступ: свободный | Студентов: 4078 / 1033 | Оценка: 4.66 / 4.45 | Длительность: 54:13:00

Темы: Математика, Экономика

Специальности: Экономист

|

Вам нравится? Нравится 61 студенту

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аппроксимация и регрессия. Соотношение (1) дает решение задачи аппроксимации. Поясним, как эта задача соотносится с нахождением регрессии. Согласно [ [ 1.19 ] ] для случайной величины $(\xi, \eta)$ со значениями в $X\times Y$ регрессией $\eta$ на $\xi$ относительно меры близости естественно назвать решение задачи

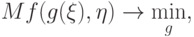$Mf(g(\xi),\eta)\rightarrow\min_{g},$

( 2)

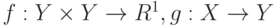где $f:Y\times Y \rightarrow R^1, g:X\rightarrow Y$ , минимум берется по множеству всех измеримых функций.

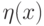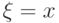Можно исходить и из другого определения. Для каждого $x\in X$ рассмотрим случайную величину $\eta(x)$ , распределение которой является условным распределением $\eta$ при условии $\xi=x$ . В соответствии с определением математического ожидания в пространстве общей природы назовем условным математическим ожиданием решение экстремальной задачи

$M(\eta|\xi=x)=Arg\min\{Mf(y,\eta(x)),y\in Y\}.$

Оказывается, при обычных предположениях измеримости решение задачи (2) совпадает с $M(\eta|\xi=x)$ . (Внутриматематические уточнения типа "равенство имеет место почти всюду" здесь опущены.)

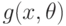Если заранее известно, что условное математическое ожидание $M(\eta|\xi=x)$ принадлежит некоторому параметрическому семейству $g(x,\theta)$ , то задача нахождения регрессии сводится к оцениванию параметра $\theta$ в соответствии с рассмотренной выше второй постановкой вероятностной теории параметрической регрессии. Если же нет оснований считать, что регрессия принадлежит параметрическому семейству, то можно использовать непараметрические оценки регрессии. Они строятся с помощью непараметрических оценок плотности (см. "Описание данных" ).

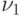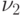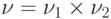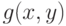Пусть $\nu_1$ - мера в , $\nu_2$ - мера в , а их прямое произведение $\nu=\nu_1\times\nu_2$ - мера в $X\times Y$ . Пусть g(x,y) - плотность случайного элемента $(\xi,\eta)$ по мере $\nu$ . Тогда условная плотность g(y|x) распределения $\eta$ при условии $\xi=х$ имеет вид

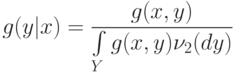$g(y|x)=\frac{g(x,y)}{\int\limits_Y g(x,y)\nu_2(dy)}$

( 3)

(в предположении, что интеграл в знаменателе отличен от 0). Следовательно,

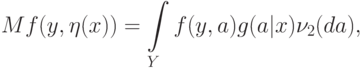
$Mf(y,\eta(x))=\int\limits_Y f(y,a)g(a|x)\nu_2(da),$

а потому

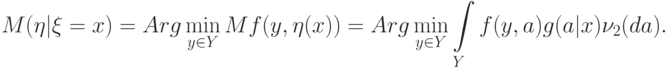
$M(\eta|\xi=x)=Arg\min_{y\in Y} Mf(y,\eta(x))= Arg\min_{y\in Y}\int\limits_Y f(y,a)g(a|x)\nu_2(da).$

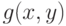Заменяя g(x,y) в (3) непараметрической оценкой плотности 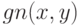gn(x,y) , получаем оценку условной плотности

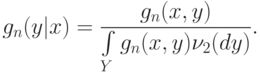$g_n(y|x)=\frac{g_n(x,y)}{\int\limits_Y g_n(x,y)\nu_2(dy)}.$

( 4)

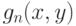Если g_n(x,y) - состоятельная оценка 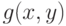g(x,y) , то числитель (4) сходится к числителю (3). Сходимость знаменателя (4) к знаменателю (3) обосновывается с помощью предельной теории статистик интегрального типа (см. "Проверка гипотез" ). В итоге получаем утверждение о состоятельности непараметрической оценки (4) условной плотности (3).

Непараметрическая оценка регрессии ищется как M_n(\eta|\xi=x)=Arg\min_{y\in Y}\int\limits_Y f(y,a)g_n(a|x)\nu_2(da).

Состоятельность этой оценки следует из приведенных выше общих результатов об асимптотическом поведении решений экстремальных статистических задач.

Применение к методу главных компонент. Исходные данные - набор векторов 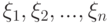$\xi_1,\xi_2,...,\xi_n$ , лежащих в евклидовом пространстве 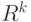R^k размерности . Цель состоит в снижении размерности, т.е. в уменьшении числа рассматриваемых показателей. Для этого берут всевозможные линейные ортогональные нормированные центрированные комбинации исходных показателей, получают новых показателей, из них берут первые , где m < k (подробности см. в "Многомерный статистический анализ" ). Матрицу преобразования выбирают так, чтобы максимизировать информационный функционал

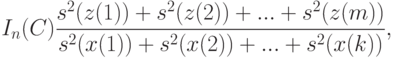$I_n(C)\frac{s^2(z(1))+s^2(z(2))+...+s^2(z(m))}{s^2(x(1))+s^2(x(2))+...+s^2(x(k))},$

( 5)

где

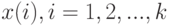, - исходные показатели; исходные данные имеют вид 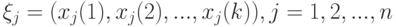$\xi_j=(x_j(1),x_j(2), ..., x_j(k)), j=1,2,...,n$ ; при этом 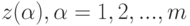$z(\alpha), \alpha= 1,2,...,m$ , - комбинации исходных показателей, полученные с помощью матрицы

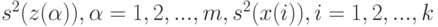. Наконец, $s^2(z(\alpha)), \alpha=1,2,...,m, s^2(x(i)), i=1,2,...,k$ , - выборочные дисперсии переменных, указанных в скобках.

Укажем подробнее, как новые показатели (главные компоненты) 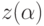$z(\alpha)$ строятся по исходным показателям x(i) с помощью матрицы :

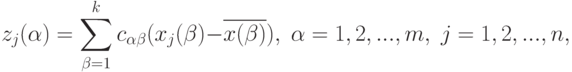
$z_j(\alpha)=\sum_{\beta=1}^k c_{\alpha\beta}(x_j(\beta)-\overline{x(\beta)}),\;\alpha=1,2,...,m,\;j=1,2,...,n,$

где

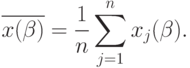
$\overline{x(\beta)}=\frac{1}{n}\sum_{j=1}^n x_j(\beta).$

Матрица $C=||c_{\alpha\beta}||$ порядка $m\times k$ такова, что

$\sum_{\beta=1}^k c_{\alpha\beta}^2=1, \alpha=1,2,...,m$

( 6)

(нормированность),

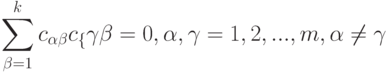$\sum_{\beta=1}^k c_{\alpha\beta}c_\{\gamma\beta}=0, \alpha,\gamma=1,2,...,m, \alpha\ne\gamma$

( 7)

(ортогональность).

Решением основной задачи метода главных компонент является

$C_n=Arg\min(-I_n(C)),$

где минимизируемая функция определена формулой (5), а минимизация проводится по всем матрицам

, удовлетворяющим условиям (6) и (7).

Вычисление матрицы C_n - задача детерминированного анализа данных. Однако, как и в иных случаях, например, для медианы Кемени, возникает вопрос об асимптотическом поведении C_n . Является ли решение основной задачи метода главных компонент устойчивым, т.е. существует ли предел C_n при $n\rightarrow\infty$ ? Чему равен этот предел?

Ответ, как обычно, может быть дан только в вероятностной теории. Пусть 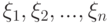$\xi_1,\xi_2,...,\xi_n$ - независимые одинаково распределенные случайные векторы. Положим

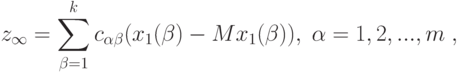
$z_{\infty}=\sum_{\beta=1}^k c_{\alpha\beta}(x_1(\beta)-Mx_1(\beta)),\;\alpha=1,2,...,m\;,$

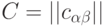где матрица $C=||c_{\alpha\beta}||$ удовлетворяет условиям (6) и (7). Введем функцию от матрицы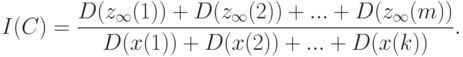

$I(C)=\frac{D(z_{\infty}(1))+D(z_{\infty}(2))+...+D(z_{\infty}(m))}{D(x(1))+D(x(2))+...+D(x(k))}.$

Легко видеть, что при $n\rightarrow\infty$ и любом C

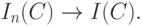
$I_n(C)\rightarrow I(C).$

Рассмотрим решение предельной экстремальной задачи

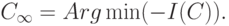
$C_{\infty}=Arg\min(-I(C)).$

Естественно ожидать, что

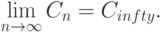
$\lim_{n\rightarrow\infty} C_n=C_{infty}.$

Действительно, это соотношение вытекает из приведенных выше общих результатов об асимптотическом поведении решений экстремальных статистических задач.

Таким образом, теория, развитая для пространств произвольной природы, позволяет единообразным образом изучать конкретные процедуры прикладной статистики.

Дальше >>

Авторизоваться

Прикладная статистика

Оценивание

Вопросы и ответы