|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Описание данных
5.5. Средние и законы больших чисел
Законы больших чисел состоят в том, что эмпирические средние сходятся к теоретическим. В классическом варианте: выборочное среднее арифметическое при определенных условиях сходится по вероятности при росте числа слагаемых к математическому ожиданию. На основе законов больших чисел обычно доказывают состоятельность различных статистических оценок. В целом эта тематика занимает заметное место в теории вероятностей и математической статистике.
Однако математический аппарат при этом основан на свойствах сумм случайных величин (векторов, элементов линейных пространств). Следовательно, он не пригоден для изучения вероятностных и статистических проблем, связанных со случайными объектами нечисловой природы. Это такие объекты, как бинарные отношения, нечеткие множества, вообще элементы пространств без векторной структуры. Объекты нечисловой природы все чаще встречаются в прикладных исследованиях. Много конкретных примеров приведено выше в настоящей лекции. Поэтому представляется полезным получение законов больших чисел в пространствах нечисловой природы. Необходимо решить следующие задачи:
- определить понятие эмпирического среднего;
- определить понятие теоретического среднего;
- ввести понятие сходимости эмпирических средних к теоретическому;
- доказать при тех или иных комплексах условий сходимость эмпирических средних к теоретическому;
- получить метод обоснования состоятельности различных статистических оценок, обобщив это доказательство;
- описать способы применения полученных результатов при решении конкретных задач.
Ввиду принципиальной важности рассматриваемых результатов приводим доказательство закона больших чисел, а также результаты компьютерного анализа множества эмпирических средних.
Определения средних величин. Пусть  - пространство произвольной природы,
- пространство произвольной природы,  - его элементы. Чтобы ввести эмпирическое среднее для
- его элементы. Чтобы ввести эмпирическое среднее для  будем использовать действительнозначную (т.е. с числовыми значениями) функцию
будем использовать действительнозначную (т.е. с числовыми значениями) функцию 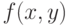 двух переменных со значениями в
двух переменных со значениями в  . В стандартных математических обозначениях:
. В стандартных математических обозначениях:  . Величина
. Величина 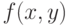 интерпретируется как показатель различия между
интерпретируется как показатель различия между  и
и  : чем
: чем 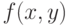 больше, тем
больше, тем  и
и  сильнее различаются. В качестве
сильнее различаются. В качестве  можно использовать расстояние в
можно использовать расстояние в  , квадрат расстояния и т.п.
, квадрат расстояния и т.п.
Определение 1. Средней величиной для совокупности  (относительно меры различия
(относительно меры различия  ), обозначаемой любым из трех способов:
), обозначаемой любым из трех способов:

 |
( 1) |
Это определение согласуется с классическим: если 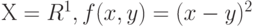 , то
, то  - выборочное среднее арифметическое. Если же
- выборочное среднее арифметическое. Если же  , то при
, то при  имеем
имеем  , при
, при  эмпирическое среднее является отрезком
эмпирическое среднее является отрезком ![[x(k), x(k+1)]](/sites/default/files/tex_cache/8d6fa6f9f0cf14d3e9424c199fa364eb.png) . Здесь через
. Здесь через  обозначен
обозначен  -ый член вариационного ряда, построенного по
-ый член вариационного ряда, построенного по  , т.е.
, т.е.  -я порядковая статистика. Таким образом, при
-я порядковая статистика. Таким образом, при  решение задачи (1) дает естественное определение выборочной медианы.
Правда, несколько отличающееся от определения, предлагаемого в курсе "Общей теории статистики", в котором при
решение задачи (1) дает естественное определение выборочной медианы.
Правда, несколько отличающееся от определения, предлагаемого в курсе "Общей теории статистики", в котором при 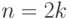 медианой называют полусумму двух центральных членов вариационного ряда
медианой называют полусумму двух центральных членов вариационного ряда 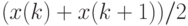 . Иногда
. Иногда 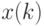 называют левой медианой, а
называют левой медианой, а 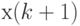 - правой [
[
1.15
]
].
- правой [
[
1.15
]
].
Решением задачи (1) является множество 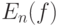 , которое может быть пустым, состоять из одного или многих элементов. Выше приведен пример, когда решением является отрезок. Если
, которое может быть пустым, состоять из одного или многих элементов. Выше приведен пример, когда решением является отрезок. Если  , а среднее арифметическое выборки равно
, а среднее арифметическое выборки равно 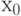 , то
, то 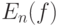 пусто.
пусто.
При моделировании реальных ситуаций часто можно принять, что  состоит из конечного числа элементов. Тогда множество
состоит из конечного числа элементов. Тогда множество 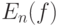 непусто - минимум на конечном множестве всегда достигается.
непусто - минимум на конечном множестве всегда достигается.
Понятия случайного элемента 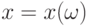 со значениями в
со значениями в  , его распределения, независимости случайных элементов используем согласно предыдущему пункту настоящей лекции, т.е. каноническому справочнику Ю.В. Прохорова и Ю.А. Розанова [
[
2.16
]
]. Будем считать, что функция
, его распределения, независимости случайных элементов используем согласно предыдущему пункту настоящей лекции, т.е. каноническому справочнику Ю.В. Прохорова и Ю.А. Розанова [
[
2.16
]
]. Будем считать, что функция  измерима относительно
измерима относительно  -алгебры, участвующей в определении случайного элемента
-алгебры, участвующей в определении случайного элемента 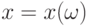 . Тогда
. Тогда 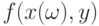 при фиксированном y является действительнозначной случайной величиной. Предположим, что она имеет математическое ожидание.
при фиксированном y является действительнозначной случайной величиной. Предположим, что она имеет математическое ожидание.
Определение 2. Теоретическим средним 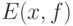 (другими словами, математическим ожиданием) случайного элемента
(другими словами, математическим ожиданием) случайного элемента 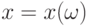 относительно меры различия
относительно меры различия  называется решение оптимизационной задачи
называется решение оптимизационной задачи
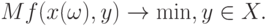 |
( 2) |
Это определение, как и для эмпирических средних, согласуется с классическим. Если 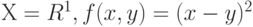 , то
, то 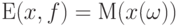 - обычное математическое ожидание. При этом
- обычное математическое ожидание. При этом  - дисперсия случайной величины
- дисперсия случайной величины 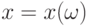 . Если же
. Если же  , то
, то ![E(x,f) = [a,b]](/sites/default/files/tex_cache/6b0ca7c8b9edfd2e62b6c23954396d51.png) , где
, где  , где
, где 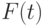 - функция распределения случайной величины
- функция распределения случайной величины 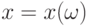 . Если график
. Если график 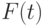 имеет плоский участок на уровне
имеет плоский участок на уровне  , то медиана - теоретическое среднее в смысле определения 2 - является отрезком. В классическом случае обычно говорят, что каждый элемент отрезка
, то медиана - теоретическое среднее в смысле определения 2 - является отрезком. В классическом случае обычно говорят, что каждый элемент отрезка ![[a; b]](/sites/default/files/tex_cache/65c152d51ed08a1761f5a8cb653eafe5.png) является одним из возможных значений медианы.
Поскольку наличие указанного плоского участка - исключительный случай, то обычно решением задачи (2) является множество из одного элемента
является одним из возможных значений медианы.
Поскольку наличие указанного плоского участка - исключительный случай, то обычно решением задачи (2) является множество из одного элемента 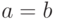 - классическая медиана распределения случайной величины
- классическая медиана распределения случайной величины 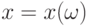 .
.
Теоретическое среднее  можно определить лишь тогда, когда
можно определить лишь тогда, когда 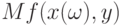 существует при всех
существует при всех 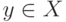 . Оно может быть пустым множеством, например, если
. Оно может быть пустым множеством, например, если  . И то, и другое исключается, если
. И то, и другое исключается, если  конечно. Однако и для конечных
конечно. Однако и для конечных  теоретическое среднее может состоять не из одного, а из многих элементов. Отметим, однако, что в множестве всех распределений вероятностей на
теоретическое среднее может состоять не из одного, а из многих элементов. Отметим, однако, что в множестве всех распределений вероятностей на  подмножество тех распределений, для которых
подмножество тех распределений, для которых 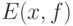 состоит более чем из одного элемента, имеет коразмерность 1, поэтому основной является ситуация, когда множество
состоит более чем из одного элемента, имеет коразмерность 1, поэтому основной является ситуация, когда множество 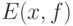 содержит единственный элемент [
[
1.15
]
].
содержит единственный элемент [
[
1.15
]
].
Существование средних величин. Под существованием средних величин будем понимать непустоту множеств решений соответствующих оптимизационных задач.
Если  состоит из конечного числа элементов, то минимум в задачах (1) и (2) берется по конечному множеству. А потому, как уже отмечалось, эмпирические и теоретические средние существуют.
состоит из конечного числа элементов, то минимум в задачах (1) и (2) берется по конечному множеству. А потому, как уже отмечалось, эмпирические и теоретические средние существуют.
Ввиду важности обсуждаемой темы приведем доказательства. Для строгого математического изложения нам понадобятся термины из раздела математики под названием "общая топология". Топологические термины и результаты будем использовать в соответствии с классической монографией [ [ 4.11 ] ]. Так, топологическое пространство называется бикомпактным в том и только в том случае, когда из каждого его открытого покрытия можно выбрать конечное подпокрытие [ [ 4.11 ] , с.183].
Теорема 1. Пусть  - бикомпактное пространство, функция
- бикомпактное пространство, функция  непрерывна на
непрерывна на  (в топологии произведения). Тогда эмпирическое и теоретическое средние существуют.
(в топологии произведения). Тогда эмпирическое и теоретическое средние существуют.
Доказательство. Функция  от y непрерывна, сумма непрерывных функций непрерывна, непрерывная функция на бикомпакте достигает своего минимума, откуда и следует заключение теоремы относительно эмпирического среднего.
от y непрерывна, сумма непрерывных функций непрерывна, непрерывная функция на бикомпакте достигает своего минимума, откуда и следует заключение теоремы относительно эмпирического среднего.
Перейдем к теоретическому среднему. По теореме Тихонова [
[
4.11
]
, с.194] из бикомпактности  вытекает бикомпактность
вытекает бикомпактность  . Для каждой точки
. Для каждой точки  из
из 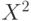 рассмотрим
рассмотрим  - окрестность в
- окрестность в 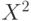 в смысле показателя различия
в смысле показателя различия  , т.е. множество
U(x,y)=\{(x',y'):|f(x,y)-f(x',y')|<\varepsilon/2\}.
, т.е. множество
U(x,y)=\{(x',y'):|f(x,y)-f(x',y')|<\varepsilon/2\}.
Поскольку  непрерывна, то множества
непрерывна, то множества  открыты в рассматриваемой топологии в
открыты в рассматриваемой топологии в 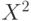 . По теореме Уоллеса [
[
4.11
]
, с.193] существуют открытые (в
. По теореме Уоллеса [
[
4.11
]
, с.193] существуют открытые (в  ) множества
) множества 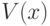 и
и  , содержащие
, содержащие  и
и  соответственно и такие, что их декартово произведение
соответственно и такие, что их декартово произведение  целиком содержится внутри
целиком содержится внутри 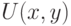 .
.
Рассмотрим покрытие 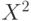 открытыми множествами
открытыми множествами  . Из бикомпактности
. Из бикомпактности 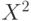 вытекает существование конечного подпокрытия
вытекает существование конечного подпокрытия  . Для каждого
. Для каждого  из
из  рассмотрим все декартовы произведения
рассмотрим все декартовы произведения  , куда входит точка
, куда входит точка 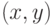 при каком-либо
при каком-либо  . Таких декартовых произведений и их первых множителей
. Таких декартовых произведений и их первых множителей  конечное число. Возьмем пересечение таких первых множителей
конечное число. Возьмем пересечение таких первых множителей  и обозначим его
и обозначим его  . Это пересечение открыто, как пересечение конечного числа открытых множеств, и содержит точку
. Это пересечение открыто, как пересечение конечного числа открытых множеств, и содержит точку  . Из покрытия бикомпактного пространства
. Из покрытия бикомпактного пространства  открытыми множествами
открытыми множествами  выберем открытое подпокрытие
выберем открытое подпокрытие 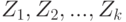 .
.
Покажем, что если  и
и 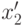 принадлежат одному и тому же
принадлежат одному и тому же 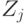 при некотором
при некотором 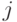 , то
, то
 |
( 3) |
Пусть  при некотором
при некотором  . Пусть
. Пусть  , - совокупность всех тех исходных декартовых произведений из системы
, - совокупность всех тех исходных декартовых произведений из системы  , куда входят точки
, куда входят точки  при различных
при различных  . Покажем, что их объединение содержит также точки
. Покажем, что их объединение содержит также точки 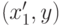 и
и  при всех
при всех  . Действительно, если
. Действительно, если 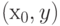 входит в
входит в  , то y входит в
, то y входит в 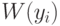 , а
, а  и
и 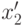 вместе с
вместе с  входят в
входят в  , поскольку
, поскольку 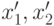 и
и  входят в
входят в 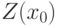 . Таким образом,
. Таким образом, 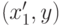 и
и  принадлежат
принадлежат  , а потому согласно определению
, а потому согласно определению 

Поскольку 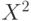 - бикомпактное пространство, то функция
- бикомпактное пространство, то функция  ограничена на
ограничена на 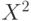 , а потому существует математическое ожидание
, а потому существует математическое ожидание 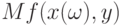 для любого случайного элемента
для любого случайного элемента 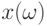 , удовлетворяющего приведенным выше условиям согласования топологии, связанной с
, удовлетворяющего приведенным выше условиям согласования топологии, связанной с  , и измеримости, связанной с
, и измеримости, связанной с 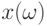 . Если
. Если  и
и 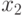 принадлежат одному открытому множеству
принадлежат одному открытому множеству 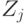 , то
, то
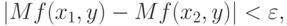
 |
( 4) |
 . Поскольку непрерывная функция на бикомпактном множестве достигает своего минимума, т.е. существуют такие точки
. Поскольку непрерывная функция на бикомпактном множестве достигает своего минимума, т.е. существуют такие точки 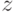 , на которых
, на которых  , то теорема 1 доказана.
, то теорема 1 доказана.В ряде интересных для приложений ситуаций  не является бикомпактным пространством. Например, если
не является бикомпактным пространством. Например, если  . В этих случаях приходится наложить на показатель различия
. В этих случаях приходится наложить на показатель различия  некоторые ограничения, например, так, как это сделано в теореме 2.
некоторые ограничения, например, так, как это сделано в теореме 2.
Теорема 2. Пусть  - топологическое пространство, непрерывная (в топологии произведения) функция
- топологическое пространство, непрерывная (в топологии произведения) функция  неотрицательна, симметрична (т.е.
неотрицательна, симметрична (т.е.  для любых
для любых  и
и  из
из  ), существует число
), существует число 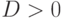 такое, что при всех
такое, что при всех 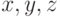 из
из 
 |
( 5) |
Пусть в  существует точка
существует точка  такая, что при любом положительном
такая, что при любом положительном  множество
множество  является бикомпактным. Пусть для случайного элемента
является бикомпактным. Пусть для случайного элемента 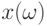 , согласованного с топологией в рассмотренном выше смысле, существует
, согласованного с топологией в рассмотренном выше смысле, существует  .
.
Тогда существуют (т.е. непусты) математическое ожидание 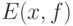 и эмпирические средние
и эмпирические средние 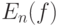 .
.
Замечание. Условие (5) - некоторое обобщение неравенства треугольника. Например, если 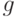 - метрика в
- метрика в  , а
, а  при некотором натуральном
при некотором натуральном  , то для
, то для  выполнено соотношение (5) с
выполнено соотношение (5) с  .
.
Доказательство. Рассмотрим функцию 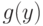 , определенную формулой (4). Имеем
, определенную формулой (4). Имеем
 |
( 6) |
Поскольку по условию теоремы  существует, а потому конечно, то из оценки (6) следует существование и конечность
существует, а потому конечно, то из оценки (6) следует существование и конечность 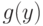 при всех
при всех  из
из  . Докажем непрерывность этой функции.
. Докажем непрерывность этой функции.
Рассмотрим шар (в смысле меры различия  ) радиуса
) радиуса  с центром в
с центром в  :
:

В соответствии с условием теоремы 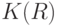 как подпространство топологического пространства
как подпространство топологического пространства  является бикомпактным. Рассмотрим произвольную точку
является бикомпактным. Рассмотрим произвольную точку  из
из  . Справедливо разложение
. Справедливо разложение

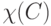 - индикатор множества
- индикатор множества  . Следовательно,
. Следовательно, |
( 7) |
Рассмотрим второе слагаемое в (7). В силу (5)
 |
( 8) |
Возьмем математическое ожидание от обеих частей (8):
 |
( 9) |
В правой части (9) оба слагаемых стремятся к 0 при безграничном возрастании  : первое - в силу того, что
: первое - в силу того, что
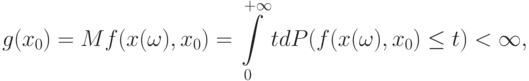
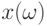 сосредоточено на
сосредоточено на  и
и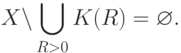
Пусть  - такая окрестность
- такая окрестность  (т.е. открытое множество, содержащее
(т.е. открытое множество, содержащее  ), для которой
), для которой

Имеем
 |
( 10) |
В силу (9) и (10) при безграничном возрастании 
 |
( 11) |
 . Пусть
. Пусть 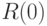 таково, что левая часть (11) меньше
таково, что левая часть (11) меньше 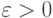 при
при  и, кроме того,
и, кроме того,  . Тогда при
. Тогда при 
 |
( 12) |
Нас интересует поведение выражения в правой части формулы (12) при  . Рассмотрим
. Рассмотрим 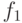 - сужение функции
- сужение функции  на замыкание декартова произведения множеств
на замыкание декартова произведения множеств  , и случайный элемент
, и случайный элемент 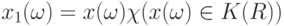 . Тогда
. Тогда

 , а непрерывность функции
, а непрерывность функции 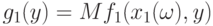 была доказана в теореме 1. Последнее означает, что существует окрестность
была доказана в теореме 1. Последнее означает, что существует окрестность 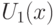 точки x такая, что
точки x такая, что |
( 13) |
 . Из (12) и (13) вытекает, что при
. Из (12) и (13) вытекает, что при 

 .
.Докажем существование математического ожидания 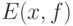 . Пусть
. Пусть 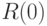 таково, что
таково, что
 |
( 14) |
Пусть  - некоторая константа, значение которой будет выбрано позже. Рассмотрим точку
- некоторая константа, значение которой будет выбрано позже. Рассмотрим точку  из множества
из множества  - дополнения
- дополнения  , т.е. из внешности шара радиуса
, т.е. из внешности шара радиуса  с центром в
с центром в  . Пусть
. Пусть  . Тогда имеем
. Тогда имеем

 |
( 15) |
Выбирая  достаточно большим, получим с учетом условия (14), что при
достаточно большим, получим с учетом условия (14), что при  справедливо неравенство
справедливо неравенство
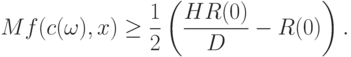 |
( 16) |
Можно выбрать  так, чтобы правая часть (16) превосходила
так, чтобы правая часть (16) превосходила  .
.
Сказанное означает, что  достаточно искать внутри бикомпактного множества
достаточно искать внутри бикомпактного множества  . Из непрерывности функции
. Из непрерывности функции 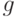 вытекает, что ее минимум достигается на указанном бикомпактном множестве, а потому - и на всем
вытекает, что ее минимум достигается на указанном бикомпактном множестве, а потому - и на всем  . Существование (непустота) теоретического среднего
. Существование (непустота) теоретического среднего 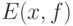 доказана.
доказана.
Докажем существование эмпирического среднего 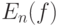 . Есть искушение проводить его дословно так же, как и доказательство существования математического ожидания
. Есть искушение проводить его дословно так же, как и доказательство существования математического ожидания 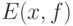 , лишь с заменой 1/2 в формуле (16) на частоту попадания элементов выборки
, лишь с заменой 1/2 в формуле (16) на частоту попадания элементов выборки  в шар
в шар  . Эта частота, очевидно, стремится к вероятности попадания случайного элемента
. Эта частота, очевидно, стремится к вероятности попадания случайного элемента 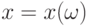 в
в  , большей 1/2 в соответствии с (14). Однако это рассуждение показывает лишь, что вероятность непустоты
, большей 1/2 в соответствии с (14). Однако это рассуждение показывает лишь, что вероятность непустоты 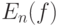 стремится к 1 при безграничном росте объема выборки. Точнее, оно показывает, что
стремится к 1 при безграничном росте объема выборки. Точнее, оно показывает, что

Поэтому пойдем другим путем, не опирающимся к тому же на вероятностную модель выборки. Положим
 |
( 17) |
Если  входит в дополнение шара
входит в дополнение шара  , то аналогично (15) имеем
, то аналогично (15) имеем
 |
( 18) |
При достаточно большом  из (17) и (18) следует, что
из (17) и (18) следует, что

Следовательно,  достаточно искать на
достаточно искать на  . Заключение теоремы 2 следует из того, что на бикомпактном пространстве
. Заключение теоремы 2 следует из того, что на бикомпактном пространстве  минимизируется непрерывная функция.
минимизируется непрерывная функция.
Теорема 2 полностью доказана.
