|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Различные виды статистических данных
Аксиоматическое введение метрики в пространстве неотрицательных суммируемых функций. Рассмотрим пространство 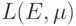 неотрицательных суммируемых функций на множестве
неотрицательных суммируемых функций на множестве 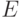 с мерой
с мерой 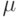 . Далее в настоящем пункте будем рассматривать только функции из
. Далее в настоящем пункте будем рассматривать только функции из 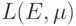 . Интегрирование всюду проводится по пространству
. Интегрирование всюду проводится по пространству 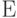 и по мере
и по мере 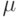 . Будем писать
. Будем писать  или
или  , если указанные соотношения справедливы почти всюду по
, если указанные соотношения справедливы почти всюду по 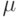 на
на 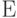 (т.е. могут нарушаться лишь на множестве нулевой меры).
(т.е. могут нарушаться лишь на множестве нулевой меры).
Аксиоматически введем расстояние в пространстве 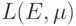 (изложение следует работе [
[
1.18
]
]). Обозначим
(изложение следует работе [
[
1.18
]
]). Обозначим 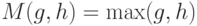 и
и 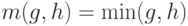 . Пусть
. Пусть 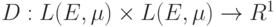 - тот основной объект изучения, аксиомы для которого будут сейчас сформулированы.
- тот основной объект изучения, аксиомы для которого будут сейчас сформулированы.
Аксиома 1. Если 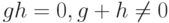 , то
, то 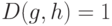 .
.
Аксиома 2. Если 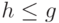 , то
, то 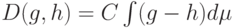 , где множитель
, где множитель  не зависит от
не зависит от  , т.е.
, т.е. 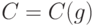 .
.
 . Из аксиом 1 и 2 следует, что для
. Из аксиом 1 и 2 следует, что для 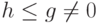 имеем
имеем
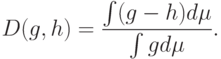
Для доказательства заметим, что по аксиоме 1 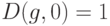 , а по аксиоме 2
, а по аксиоме 2  , откуда
, откуда 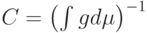 . Подставляя это соотношение в аксиому 2, получаем заключение леммы.
. Подставляя это соотношение в аксиому 2, получаем заключение леммы.
Требование согласованности расстояния в пространстве 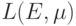 с отношением "находиться между" приводит, как и ранее для расстояния
с отношением "находиться между" приводит, как и ранее для расстояния 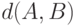 , к следующей аксиоме.
, к следующей аксиоме.
Аксиома 3. Для любых 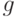 и
и  справедливо равенство
справедливо равенство 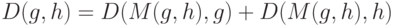 .
.
Замечание. В ряде реальных ситуаций естественно считать, что наибольшее расстояние между элементами пространства множеств (которое без ограничения общности можно положить равным 1), т.е. наибольшее несходство, соответствует множествам, не имеющим общих элементов. Расстояние, введенное в теореме 3 (формула (1)), этому условию не удовлетворяет. Поэтому в пространстве множеств была аксиоматически введена [ [ 1.21 ] ] так называемая D-метрика (от dissimilarity (англ.) - несходство), для которого это условие выполнено. Она имеет вид:
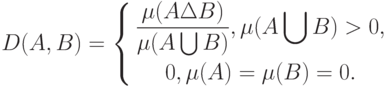 |
( 7) |
Приведенные выше аксиомы являются обобщениями соответствующих аксиом для 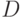 -метрики в пространстве множеств.
-метрики в пространстве множеств.
Теорема 7. Из аксиом 1–3 следует, что
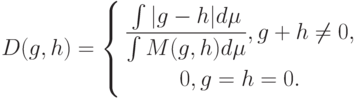 |
( 8) |
Доказательство. Поскольку
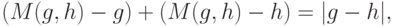
то заключение теоремы 7 при 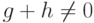 вытекает из леммы и аксиомы 3. Из аксиомы 2 при
вытекает из леммы и аксиомы 3. Из аксиомы 2 при  следует, что
следует, что 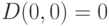 . Легко видеть, что функция
. Легко видеть, что функция 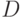 , заданная формулой (8), удовлетворяет аксиомам 1–3 и, кроме того,
, заданная формулой (8), удовлетворяет аксиомам 1–3 и, кроме того, 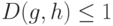 при любых
при любых 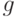 и
и  .
.
Замечание. Если 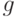 и
и  - индикаторные функции множеств, то формула (8) переходит в формулу (7). Если
- индикаторные функции множеств, то формула (8) переходит в формулу (7). Если 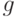 и
и  - функции принадлежности нечетких множеств, то формула (8) задает метрику в пространстве нечетких множеств, а именно,
- функции принадлежности нечетких множеств, то формула (8) задает метрику в пространстве нечетких множеств, а именно, 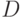 -метрику в этом пространстве [
[
1.21
]
].
-метрику в этом пространстве [
[
1.21
]
].
Теорема 8. Функция  , определенная формулой (8), является метрикой в
, определенная формулой (8), является метрикой в 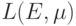 (при отождествлении функций, отличающихся лишь на множестве нулевой меры), причем
(при отождествлении функций, отличающихся лишь на множестве нулевой меры), причем 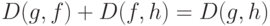 тогда и только тогда, когда
тогда и только тогда, когда 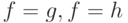 или
или 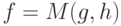 .
.
Доказательство. Обратимся к определению метрики. Для рассматриваемой функции непосредственно очевидна справедливость условий неотрицательности и симметричности. Очевидна и эквивалентность условия 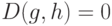 равенству
равенству  . Остается доказать неравенство треугольника и установить, когда оно обращается в равенство.
. Остается доказать неравенство треугольника и установить, когда оно обращается в равенство.
Без ограничения общности можно считать, что рассматриваемые расстояния задаются верхней строкой формулы (8) и кроме того,
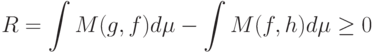
(частные случаи с использованием нижней строки формулы (8) рассматриваются элементарно, а справедливости последнего неравенства можно добиться заменой обозначений функций - элементов пространства 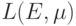 ). Тогда
). Тогда
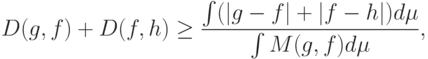 |
( 9) |
причем равенство имеет место тогда и только тогда, когда  или
или  . Положим
. Положим

Ясно, что  и
и
 |
( 10) |
Если 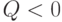 , то очевидно, что неравенство треугольника выполнено, причем неравенство является строгим. Рассмотрим случай
, то очевидно, что неравенство треугольника выполнено, причем неравенство является строгим. Рассмотрим случай 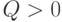 .
.
Воспользуемся следующим элементарным фактом: если 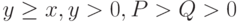 , то
, то
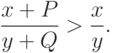 |
( 11) |
Из соотношений (10) и (11) вытекает, что для доказательства неравенства треугольника достаточно показать, что 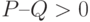 .
.
Рассмотрим
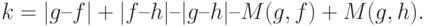
Применяя равенство 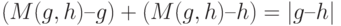 к слагаемым, заключенным в фигурные скобки, получаем, что
к слагаемым, заключенным в фигурные скобки, получаем, что
![k=M(f,h)+[M(g,f)+M(f,h)–M(g,h)–2f].](/sites/default/files/tex_cache/ac0a0750341c91e07852bc9d796816df.png)
Применяя соотношение
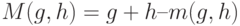 |
( 12) |
к слагаемым, заключенным в квадратные скобки, получаем, что
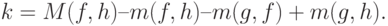
Так как 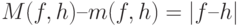 , то
, то
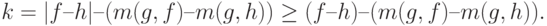 |
( 13) |
В соответствии с (12) правая часть (13) есть 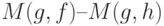 , а потому
, а потому
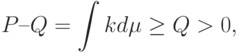
что завершает доказательство для случая 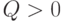 . При этом неравенство треугольника является строгим.
. При этом неравенство треугольника является строгим.
Осталось рассмотреть случай 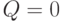 . В силу соотношений (9) и (10) неравенство треугольника выполнено. Когда оно обращается в равенство? Тривиальные случаи:
. В силу соотношений (9) и (10) неравенство треугольника выполнено. Когда оно обращается в равенство? Тривиальные случаи:  или
или  . Если же
. Если же  отлично от
отлично от 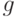 и
и  , то необходимо, чтобы
, то необходимо, чтобы  и
и  . Как легко проверить, последнее условие эквивалентно неравенствам
. Как легко проверить, последнее условие эквивалентно неравенствам
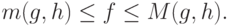 |
( 14) |
Из правого неравенства в (14) следует, что 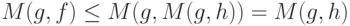 . Так как
. Так как 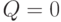 , то
, то  . Аналогичным образом из соотношений
. Аналогичным образом из соотношений
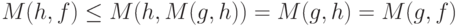
и  следует, что
следует, что  .
.
Рассмотрим измеримое множество 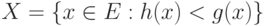 . Тогда
. Тогда 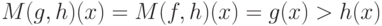 , т.е.
, т.е. 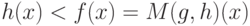 для почти всех
для почти всех 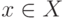 . Для почти всех
. Для почти всех 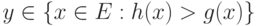 точно так же получаем
точно так же получаем 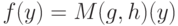 . Для почти всех
. Для почти всех 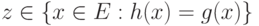 в силу (14)
в силу (14) 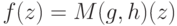 , что и завершает доказательство теоремы.
, что и завершает доказательство теоремы.
Замечание. Назовем функции 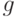 и
и  подобными, если существует число
подобными, если существует число 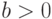 такое, что
такое, что 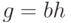 . Тогда при
. Тогда при 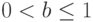 имеем
имеем 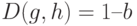 , т.е. расстояние между подобными функциями линейно зависит от коэффициента подобия. Далее, пусть
, т.е. расстояние между подобными функциями линейно зависит от коэффициента подобия. Далее, пусть 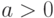 , тогда
, тогда 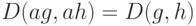 . Таким образом, метрика (8) инвариантна по отношению к преобразованиям подобия, которые образуют группу допустимых преобразований в шкале отношений. Это дает основания именовать метрику (8) метрикой подобия [
[
1.18
]
].
. Таким образом, метрика (8) инвариантна по отношению к преобразованиям подобия, которые образуют группу допустимых преобразований в шкале отношений. Это дает основания именовать метрику (8) метрикой подобия [
[
1.18
]
].
Контрольные вопросы и задачи
- Приведите примеры практического использования количественных и категоризованных данных.
- Как соотносятся группы допустимых преобразований для различных шкал измерения?
- Почему анализ нечисловых данных занимает одно из центральных мест в прикладной статистике?
- В каких случаях целесообразно применение нечетких множеств?
- Справедливо ли для нечетких множеств равенство
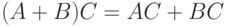 ? А равенство
? А равенство 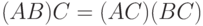 ?
? - Докажите, что для блочного расстояния (пример 4 из п.1.5) справедливо неравенство треугольника.
- Расскажите о многообразии расстояний в различных пространствах статистических данных.
- Докажите, что если
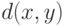 - расстояние в некотором пространстве, то
- расстояние в некотором пространстве, то 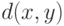 - также расстояние в этом пространстве.
- также расстояние в этом пространстве.
Темы докладов, рефератов, исследовательских работ
- Содержание первого сочинения по прикладной статистике - книги "Числа" в Библии.
- Свойства основных шкал измерения.
- Взаимосвязи различных классов объектов нечисловой природы между собой.
- Опишите с помощью нечеткого подмножества временной шкалы понятие "молодой человек" (на основе опроса 10–20 экспертов).
- Опишите с помощью теории нечеткости понятие "куча зерен" (на основе опроса 10–20 экспертов).
- Центральная роль статистики объектов произвольной природы в прикладной статистике.
- Расстояния в пространствах функций.
- Докажите, что аксиоматически введенный в п.1.6 показатель различия между множествами
 удовлетворяет неравенству треугольника.
удовлетворяет неравенству треугольника.
