|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Различные виды статистических данных
1.5. Данные и расстояния в пространствах произвольной природы
Как показано выше, исходные статистические данные могут иметь разнообразную математическую природу, являться элементами разнообразных пространств - конечномерных, функциональных, бинарных отношений, множеств, нечетких множеств и т.д. Следовательно, центральной частью прикладной статистики является статистика в пространствах произвольной природы. Эта область прикладной статистики сама по себе не используется при анализе конкретных данных. Это очевидно, поскольку конкретные данные всегда имеют вполне определенную природу. Однако общие подходы, методы, результаты статистики в пространствах произвольной природы представляют собой научный инструментарий, готовый для использования в каждой конкретной области.
Статистика в пространствах произвольной природы. Много ли общего у статистических методов анализа данных различной природы? На этот естественный вопрос можно сразу же однозначно ответить - да, очень много. Такой ответ будет постоянно подтверждаться и конкретизироваться на протяжении всего учебника. Несколько примеров приведем сразу же.
Прежде всего отметим, что понятия случайного события, вероятности, независимости событий и случайных величин являются общими для любых конечных вероятностных пространств и любых конечных областей значений случайных величин (см. лекции "Основы вероятностно-статистических методов описания неопределенностей" и "Описание данных" ). Поскольку все реальные явления и процессы описываются с помощью математических объектов из конечных множеств, сказанное выше означает, что конечных вероятностных пространств и дискретных случайных величин (точнее, величин, принимающих значения в конечном множестве) достаточно для всех практических применений. Переход к непрерывным моделям реальных явлений и процессов оправдан только тогда, когда этот переход облегчает проведение рассуждений и выкладок. Например, находить определенные интегралы зачастую проще, чем вычислять значения сумм. Не могу не отметить, что приведенные соображения о взаимосоотнесении дискретных и непрерывных математических моделей автор услышал более 30 лет назад от академика А.Н. Колмогорова (ясно, что за конкретную формулировку несет ответственность автор настоящего учебника).
Основные проблемы прикладной статистики - описание данных, оценивание, проверка гипотез - также в своей существенной части могут быть рассмотрены в рамках статистики в пространствах произвольной природы. Например, для описания данных могут быть использованы эмпирические и теоретические средние, плотности вероятностей и их непараметрические оценки, регрессионные зависимости. Правда, для этого пространства произвольной природы должны быть снабжены соответствующим математическим инструментарием - расстояниями (показателями близости, мерами различия) между элементами рассматриваемых пространств.
Популярный в настоящее время метод оценивания параметров распределений - метод максимального правдоподобия - не накладывает каких-либо ограничений на конкретный вид элементов выборки. Они могут лежать в пространстве произвольной природы. Математические условия касаются только свойств плотностей вероятности и их производных по параметрам. Аналогично положение с методом одношаговых оценок, идущим на смену методу максимального правдоподобия (см. "Оценивание" ). Асимптотику решений экстремальных статистических задач достаточно изучить для пространств произвольной природы, а затем применять в каждом конкретном случае [ [ 1.17 ] ], когда задачу прикладной статистики удается представить в оптимизационном виде. Общая теория проверки статистических гипотез также не требует конкретизации математической природы рассматриваемых элементов выборок. Это относится, например, к лемме Неймана-Пирсона или теории статистических решений. Более того, естественная область построения теории статистик интегрального типа - это пространства произвольной природы (см. "Проверка гипотез" ).
Совершенно ясно, что в конкретных областях прикладной статистики накоплено большое число результатов, относящихся именно к этим областям. Особенно это касается областей, исследования в которых ведутся сотни лет, в частности, статистики случайных величин (одномерной статистики). Однако принципиально важно указать на "ядро" прикладной статистики - статистику в пространствах произвольной природы. Если постоянно "держать в уме" это ядро, то становится ясно, что, например, многие методы непараметрической оценки плотности вероятности или кластер-анализа, использующие только расстояния между объектами и элементами выборки, относятся именно к статистике объектов произвольной природы, а не к статистике случайных величин или многомерному статистическому анализу. Следовательно, и применяться они могут во всех областях прикладной статистики, а не только в тех, в которых "родились".
Расстояния (метрики). В пространствах произвольной природы нет операции сложения, следовательно, статистические процедуры не могут быть основаны на использовании сумм. Поэтому используется другой математический инструментарий, использующий понятия типа расстояния.
Как известно, расстоянием в пространстве  называется числовая функция двух переменных
называется числовая функция двух переменных 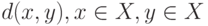 , определенная на этом пространстве, т.е. в стандартных обозначениях
, определенная на этом пространстве, т.е. в стандартных обозначениях  , где
, где 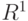 - прямая, т.е. множество всех действительных чисел. Эта функция должна удовлетворять трем условиям (иногда их называют аксиомами):
- прямая, т.е. множество всех действительных чисел. Эта функция должна удовлетворять трем условиям (иногда их называют аксиомами):
- неотрицательности:
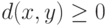 , причем
, причем 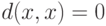 , для любых значений
, для любых значений 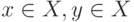 ;
; - симметричности:
 для любых
для любых 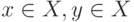 ;
; - неравенства треугольника:
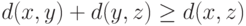 для любых значений
для любых значений  .
.
Для термина "расстояние" часто используется синоним - "метрика".
Пример 1. Если 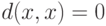 и
и 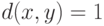 при
при  для любых значений
для любых значений 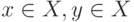 , то, как легко проверить, функция
, то, как легко проверить, функция 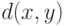 - расстояние (метрика). Такое расстояние естественно использовать в пространстве
- расстояние (метрика). Такое расстояние естественно использовать в пространстве  значений номинального признака: если два значения (например, названные двумя экспертами) совпадают, то расстояние равно 0, а если различны - то 1.
значений номинального признака: если два значения (например, названные двумя экспертами) совпадают, то расстояние равно 0, а если различны - то 1.
Пример 2. Расстояние, используемое в геометрии, очевидно, удовлетворяет трем приведенным выше аксиомам. Если  - это плоскость, а
- это плоскость, а 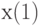 и
и 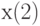 - координаты точки
- координаты точки  в некоторой прямоугольной системе координат, то эту точку естественно отождествить с двумерным вектором
в некоторой прямоугольной системе координат, то эту точку естественно отождествить с двумерным вектором 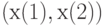 . Тогда расстояние между точками
. Тогда расстояние между точками 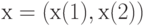 и
и 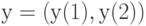 согласно известной формуле аналитической геометрии равно
согласно известной формуле аналитической геометрии равно
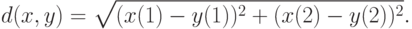
Пример 3. Евклидовым расстоянием в пространстве 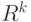 векторов вида
векторов вида 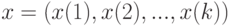 и
и 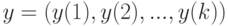 размерности
размерности  называется
называется
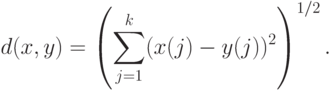
В примере 2 рассмотрен частный случай примера 3 с  .
.
Пример 4. В пространстве 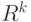 векторов размерности
векторов размерности  используют также так называемое "блочное расстояние", имеющее вид
используют также так называемое "блочное расстояние", имеющее вид
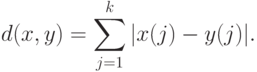
Блочное расстояние соответствует передвижению по городу, разбитому на кварталы горизонтальными и вертикальными улицами. В результате можно передвигаться только параллельно одной из осей координат.
Пример 5. В пространстве функций, элементами которого являются функции 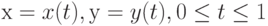 , часто используют расстояние Колмогорова
, часто используют расстояние Колмогорова
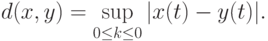
Пример 6. Пространство функций, элементами которого являются функции 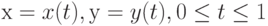 , превращают в метрическое пространство (т.е. в пространство с метрикой), вводя расстояние
, превращают в метрическое пространство (т.е. в пространство с метрикой), вводя расстояние
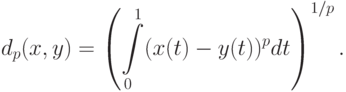
Это пространство обычно обозначают 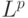 , где параметр
, где параметр 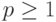 (при
(при  не выполняются аксиомы метрического пространства, в частности, аксиома треугольника).
не выполняются аксиомы метрического пространства, в частности, аксиома треугольника).
Пример 7. Рассмотрим пространство квадратных матриц порядка  . Как ввести расстояние между матрицами
. Как ввести расстояние между матрицами 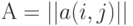 и
и 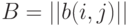 ? Можно сложить расстояния между соответствующими элементами матриц:
? Можно сложить расстояния между соответствующими элементами матриц:
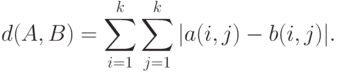
Пример 8. Предыдущий пример наводит на мысль о следующем полезном свойстве расстояний. Если на некотором пространстве определены два или больше расстояний, то их сумма - также расстояние.
Пример 9. Пусть  и
и  - множества. Расстояние между множествами можно определить формулой
- множества. Расстояние между множествами можно определить формулой
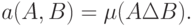
Здесь  - мера на рассматриваемом пространстве множеств,
- мера на рассматриваемом пространстве множеств,  - символ симметрической разности множеств.
- символ симметрической разности множеств.
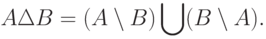
Если мера - так называемая считающая, т.е. приписывающая единичный вес каждому элементу множества, то введенное расстояние есть число несовпадающих элементов в множествах  и
и  .
.
Пример 10. Между множествами можно ввести и другое расстояние:
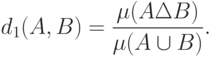
В ряде задач прикладной статистики используются функции двух переменных, для которых выполнены не все три аксиомы расстояния, а только некоторые. Их обычно называют показателями различия, поскольку чем больше различаются объекты, тем больше значение функции. Иногда в том же смысле используют термин "мера близости". Он менее удачен, поскольку большее значение функции соответствует меньшей близости.
Чаще всего отказываются от аксиомы, требующей выполнения неравенства треугольника, поскольку это требование не всегда находит обоснование в конкретной прикладной ситуации.
Пример 11. В конечномерном векторном пространстве показателем различия является
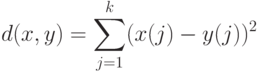
(сравните с примером 3).
Показателями различия, но не расстояниями являются такие популярные в прикладной статистике показатели, как дисперсия или средний квадрат ошибки при оценивании.
Иногда отказываются также и от аксиомы симметричности.
Пример 12. Показателем различия чисел  и
и  является
является
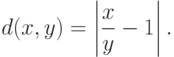
Такой показатель различия используют в ряде процедур экспертного оценивания.
Что же касается первой аксиомы расстояния, то в различных постановках прикладной статистики ее обычно принимают. Вполне естественно, что наименьший показатель различия должен достигаться, причем именно на совпадающих объектах. Имеет ли смысл это наименьшее значение делать отличным от 0? Вряд ли, поскольку всегда можно добавить одну и ту же константу ко всем значениям показателя различия и тем самым добиться выполнения первой аксиомы.
В прикладной статистике используются самые разные расстояния и показатели различия. О них пойдет речь в соответствующих разделах учебника.
