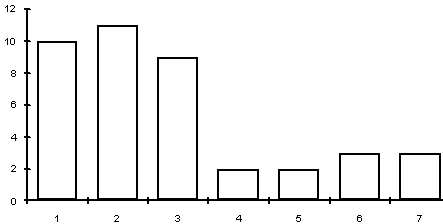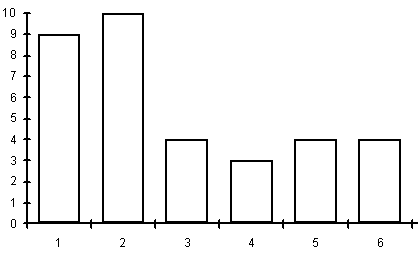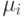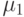|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Различные виды статистических данных
Всего было опрошено 74 человека, из них 40 - научные работники и преподаватели, 34 человека - не занятых в сфере науки и образования, в том числе 5 рабочих и 5 пенсионеров. Из всех опрошенных только один (!) считает себя богатым. Несколько типичных ответов научных работников и преподавателей приведено в табл.1.3, а аналогичные сведения для работников коммерческой сферы - в табл.1.4.
| Ответы на вопрос 3 | Ответы на вопрос 1 | Ответы на вопрос 2 | Пол |
|---|---|---|---|
| Кандидат наук | 6 | д | ж |
| Преподаватель | 6 | в | ж |
| Доцент | 6 | б | ж |
| Учитель | 60 | в | м |
| Старший научный сотрудник | 60 | д | м |
| Инженер-физик | 140 | д | ж |
| Программист | 150 | г | м |
| Научный работник | 270 | г | м |
| Ответы на вопрос 3 | Ответы на вопрос 1 | Ответы на вопрос 2 | Пол |
|---|---|---|---|
| Вице-президент банка | 600 | а | ж |
| Зам. директора банка | 300 | б | ж |
| Начальник кредитного отдела | 300 | б | м |
| Начальник отдела ценных бумаг | 60 | б | м |
| Главный бухгалтер | 120 | д | ж |
| Бухгалтер | 90 | в | ж |
| Менеджер банка | 66 | б | м |
| Начальник отдела проектирования | 60 | в | ж |
Разброс ответов на первый вопрос - от 6 до 600 тыс. руб. в месяц на человека. Результаты опроса показывают, что критерий богатства у финансовых работников в целом несколько выше, чем у научных (см. гистограммы на рис.1.1,1.2 ниже).
Опрос показал, что выявить какое-нибудь конкретное значение суммы, которая необходима "для полного счастья", пусть даже с небольшим разбросом, нельзя, что вполне естественно. Как видно из таблиц 1.3 и 1.4, денежный эквивалент богатства колеблется от 6 до 600 тыс. руб. в месяц. Подтвердилось мнение, что работники сферы образования в подавляющем большинстве причисляют свой достаток к категории "в" и ниже (81% опрошенных), в том числе к категории "д" отнесли свой достаток 57%.
Со служащими коммерческих структур и бюджетных организаций иная картина: "г" - категория 1 человек (4%), "д" - категория 4 человека (17%), "б" - категория - 46% и 1 человек "а" - категория.
Пенсионеры, что не вызывает удивления, отнесли свой доход к категории "д" (4 человека), и лишь один человек указал "г" - категорию. Рабочие же ответили так: 4 человека - "в", и один человек - "б".
Для представления общей картины в табл.1.5 приведены данные об ответах работников других профессий.
| Ответы на вопрос 3 | Ответы на вопрос 1 | Ответы на вопрос 2 | Пол |
|---|---|---|---|
| Работник торговли | 6 | б | ж |
| Дворник | 12 | в | ж |
| Водитель | 60 | в | м |
| Военнослужащий | 60 | в | м |
| Владелец бензоколонки | 120 | б | ж |
| Пенсионер | 36 | д | ж |
| Начальник фабрики | 120 | б | м |
| Хирург | 30 | в | м |
| Домохозяйка | 60 | в | м |
| Слесарь-механик | 150 | в | м |
| Юрист | 60 | б | м |
| Оператор ЭВМ | 120 | д | м |
| Работник собеса | 18 | д | ж |
| Архитектор | 150 | б | ж |
Прослеживается интересное явление: чем выше планка богатства для человека, тем к более низкой категории относительно этой планки он себя относит.
Для сводки данных естественно использовать гистограммы. Для этого необходимо сгруппировать ответы. Использовались 7 классов (интервалов):
- – до 30 тыс. руб. в месяц на человека (включительно);
- – от 30 до 60 тыс. руб.;
- – от 60 до 90 тыс. руб.;
- – от 90 до 120 тыс. руб.;
- – от 120 до 150 тыс. руб.;
- – от 150 до 180 тыс. руб;
- – более 180 тыс.
(Во всех интервалах левая граница исключена, а правая, наоборот, включена.)
Сводная информация представлена на рис.1.1 (для научных работников и преподавателей) и рис.1.2 (для всех остальных, т.е. для лиц, не занятых в сфере науки и образования - служащих иных бюджетных организаций, коммерческих структур, рабочих, пенсионеров).
Для двух выделенных групп, а также для некоторых подгрупп второй группы рассчитаны сводные средние характеристики - выборочные средние арифметические, медианы, моды. При этом медиана группы - количество тыс. руб., названное центральным по порядковому номеру опрашиваемым в возрастающем ряду ответов на вопрос 1, а мода группы - интервал, на котором столбик гистограммы - самый высокий, т.е. в него "попало" максимальное количество опрашиваемых. Результаты приведены в табл.1.6.
| Группа опрошенных | Среднее арифметическое | Медиана | Мода |
|---|---|---|---|
| Научные работники и преподаватели | 70 | 43,5 | (30; 60) |
| Лица, не занятые в сфере науки и образования | 86,4 | 120,0 | (30; 60) |
| Служащие коммерческих структур и бюджетных организаций | 107,5 | 60 | (30; 60) |
| Рабочие | 90,0 | 78,0 | - |
| Пенсионеры | 61,8 | 60,0 | - |
Построим нечеткое множество, описывающее понятие "богатый человек" в соответствии с представлениями опрошенных. Для этого составим табл.1.7 на основе рис.1.1 и рис.1.2 с учетом размаха ответов на первый вопрос.
| № п/п | Номер интервала | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Интервал, тыс. руб. в месяц | (0;6) | [6;30] | (30;60] | (60;90] | (90;120] | (120;150] | (150;180] | (180;600) | [600;+  ) ) |
| 2 | Число ответов в интервале | 0 | 19 | 21 | 13 | 5 | 6 | 7 | 2 | 1 |
| 3 | Доля ответов в интервале | 0 | 0,257 | 0,284 | 0,176 | 0,068 | 0,081 | 0,095 | 0,027 | 0,013 |
| 4 | Накопленное число ответов | 19 | 40 | 53 | 58 | 64 | 71 | 73 | 74 | |
| 5 | Накопленная доля ответов | 0 | 0,257 | 0,541 | 0,716 | 0,784 | 0,865 | 0,960 | 0,987 | 1,000 |
Пятая строка табл.1.7 задает функцию принадлежности нечеткого множества, выражающего понятие "богатый человек" в терминах его ежемесячного дохода. Это нечеткое множество является подмножеством множества из 9 интервалов, заданных в строке 2 табл.5. Или множества из 9 условных номеров {0, 1, 2, …, 8}. Эмпирическая функция распределения, построенная по выборке из ответов 74 опрошенных на первый вопрос мини-анкеты, описывает понятие "богатый человек" как нечеткое подмножество положительной полуоси.
О разработке методики ценообразования на основе теории нечетких множеств. Для оценки значений показателей, не имеющих количественной оценки, можно использовать методы нечетких множеств. Например, в диссертации П.В. Битюкова [ [ 1.2 ] ] нечеткие множества применялись при моделировании задач ценообразования на электронные обучающие курсы, используемые при дистанционном обучении. Им было проведено исследование значений фактора "Уровень качества курса" с использованием нечетких множеств. В ходе практического использования предложенной П.В. Битюковым методики ценообразования значения ряда других факторов могут также определяться с использованием теории нечетких множеств. Например, ее можно использовать для определения прогноза рейтинга специальности в вузе с помощью экспертов, а также значений других факторов, относящихся к группе "Особенности курса". Опишем подход П.В. Битюкова, как пример практического использования теории нечетких множеств.
Значение оценки, присваиваемой каждому интервалу для фактора "Уровень качества курса", определяется на универсальной шкале [0,1], где необходимо разместить значения лингвистической переменной "Уровень качества курса": НИЗКИЙ, СРЕДНИЙ, ВЫСОКИЙ. Степень принадлежности некоторого значения вычисляется как отношение числа ответов, в которых оно встречалось в определенном интервале шкалы, к максимальному (для этого значения) числу ответов по всем интервалам.
Был проведен опрос экспертов о степени влияния уровня качества электронных курсов на их потребительную ценность. Каждому эксперту в процессе опроса предлагалось оценить с позиции потребителя ценность того или иного класса курсов в зависимости от уровня качества. Эксперты давали свою оценку для каждого класса курсов по 10-ти балльной шкале (где 1 - min, 10 - max). Для перехода к универсальной шкале [0,1] все значения 10-ти балльной шкалы оценки ценности были разделены на максимальную оценку, т.е. на 10.
Используя свойства функции принадлежности, необходимо предварительно обработать данные для того, чтобы уменьшить искажения, вносимые опросом. Естественными свойствами функций принадлежности являются наличие одного максимума и гладкие, затухающие до нуля фронты. Для обработки статистических данных можно воспользоваться так называемой матрицей подсказок. Предварительно удаляются явно ошибочные элементы. Критерием удаления служит наличие нескольких нулей в строке вокруг этого элемента.
Элементы матрицы подсказок вычисляются по формуле:
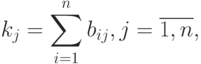
где 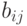 - элемент таблицы с результатами анкетирования, сгруппированными по интервалам. Матрица подсказок представляет собой строку, в которой выбирается максимальный элемент:
- элемент таблицы с результатами анкетирования, сгруппированными по интервалам. Матрица подсказок представляет собой строку, в которой выбирается максимальный элемент: 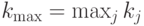 , и далее все ее элементы преобразуются по формуле:
, и далее все ее элементы преобразуются по формуле:
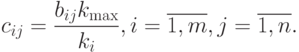
Для столбцов, где 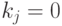 , применяется линейная аппроксимация:
, применяется линейная аппроксимация:
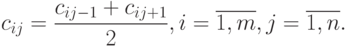
Результаты расчетов сводятся в таблицу, на основании которой строятся функции принадлежности. Для этого находятся максимальные элементы по строкам: 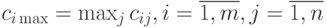 . Функция принадлежности вычисляется по формуле:
. Функция принадлежности вычисляется по формуле:  . Результаты расчетов приведены в табл.1.8.
. Результаты расчетов приведены в табл.1.8.
На рис.1.3 сплошными линиями показаны функции принадлежности значений лингвистической переменной "Уровень качества курса" после обработки таблицы, содержащей результаты опроса. Как видно из графика, функции принадлежности удовлетворяют описанным выше свойствам. Для сравнения пунктирной линией показана функция принадлежности лингвистической переменной для значения НИЗКИЙ без обработки данных.