НОУ ИНТУИТ | Прикладная статистика. Лекция 1: Различные виды статистических данных

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 09.11.2009 | Доступ: свободный | Студентов: 4091 / 1039 | Оценка: 4.66 / 4.45 | Длительность: 54:13:00

Темы: Математика, Экономика

Специальности: Экономист

|

Вам нравится? Нравится 61 студенту

| Поделиться |

Поддержать курс

| Скачать электронную книгу

1.4. Нечеткие множества - частный случай нечисловых данных

Нечеткие множества. Пусть - некоторое множество. Подмножество множества может быть задано своей характеристической функцией

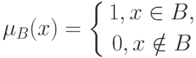$\mu_B(x)= \left \{ \begin{gathered} 1,x\in B,\\ 0,x\notin B \end{gathered} \right.$

( 1)

Что такое нечеткое множество? Обычно говорят, что нечеткое подмножество множества характеризуется своей функцией принадлежности $\mu_C:A\rightarrow [0,1]$ . Значение функции принадлежности в точке показывает степень принадлежности этой точки нечеткому множеству. Нечеткое множество описывает неопределенность, соответствующую точке х - она одновременно и входит, и не входит в нечеткое множество . 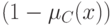За вхождение - $\mu_C(x)$ шансов, за второе - $(1-\mu_C(x))$ шансов.

Если функция принадлежности $\mu_C(x)$ имеет вид (1) при некотором , то есть обычное (четкое) подмножество . Таким образом, теория нечетких множество является не менее общей математической дисциплиной, чем обычная теория множеств, поскольку обычные множества - частный случай нечетких. Соответственно можно ожидать, что теория нечеткости, как целое, обобщает классическую математику. Однако позже мы увидим, что теория нечеткости в определенном смысле сводится к теории случайных множеств и тем самым является частью классической математики. Другими словами, по степени общности обычная математика и нечеткая математика эквивалентны. Однако для практического применения, например, в теории принятия решений описание и анализ неопределенностей с помощью теории нечетких множеств весьма плодотворны.

Обычное подмножество можно было бы отождествить с его характеристической функцией. Этого математики не делают, поскольку для задания функции (в ныне принятом подходе) необходимо сначала задать множество. Нечеткое же подмножество с формальной точки зрения можно отождествить с его функцией принадлежности. Однако термин "нечеткое подмножество" предпочтительнее при построении математических моделей реальных явлений.

Теория нечеткости является обобщением интервальной математики. Действительно, функция принадлежности

$\mu_B(x)= \left \{ \begin{gathered} 1,x\in [a,b],\\ 0,x\notin [a,b] \end{gathered} \right.$

задает интервальную неопределенность - про рассматриваемую величину известно лишь, что она лежит в заданном интервале [a,b] . Тем самым описание неопределенностей с помощью нечетких множеств является более общим, чем с помощью интервалов.

Начало современной теории нечеткости положено в 1965 г. работой американского ученого азербайджанского происхождения Л.А. Заде. К настоящему времени по этой теории опубликованы тысячи книг и статей, издается несколько международных журналов, выполнено достаточно много как теоретических, так и прикладных работ. Первая книга российского автора по теории нечеткости вышла в 1980 г. [ [ 1.16 ] ].

Л.А. Заде рассматривал теорию нечетких множеств как аппарат анализа и моделирования гуманистических систем, т.е. систем, в которых участвует человек. Его подход опирается на предпосылку о том, что элементами мышления человека являются не числа, а элементы некоторых нечетких множеств или классов объектов, для которых переход от "принадлежности" к "непринадлежности" не скачкообразен, а непрерывен. В настоящее время методы теории нечеткости используются почти во всех прикладных областях, в том числе при управлении предприятиями, качеством продукции и технологическими процессами, при описании предпочтений потребителей и варки стали.

Л.А. Заде использовал термин "fuzzy set" (нечеткое множество). На русский язык термин "fuzzy" переводили как нечеткий, размытый, расплывчатый, и даже как пушистый и туманный.

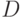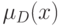Аппарат теории нечеткости громоздок. В качестве примера дадим определения теоретико-множественных операций над нечеткими множествами. Пусть и - два нечетких подмножества с функциями принадлежности $\mu_C(x)$ и $\mu_D(x)$ соответственно. Пересечением 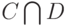$C\bigcap D$ , произведением 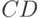, объединением 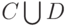$C\bigcup D$ , отрицанием 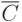$\overline{C}$ , суммой 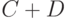C+D называются нечеткие подмножества с функциями принадлежности

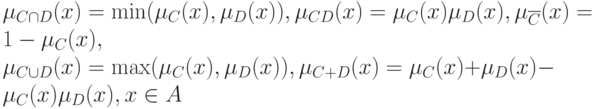
$\begin{multiline*} \mu_{C\cap D}(x)=\min(\mu_C(x),\mu_D(x)),\mu_{CD}(x)=\mu_C(x)\mu_D(x),\mu_{\overline{C}}(x)=1-\mu_C(x), \\ \mu_{C\cup D}(x)=\max(\mu_C(x),\mu_D(x)),\mu_{C+D}(x)=\mu_C(x)+\mu_D(x)-\mu_C(x)\mu_D(x),x\in A \end{multiline*}$

соответственно.

Как уже отмечалось, теория нечетких множеств в определенном смысле сводится к теории вероятностей, а именно, к теории случайных множеств. Соответствующий цикл теорем приведен ниже в "Теоретическая база прикладной статистики" . Однако при решении прикладных задач вероятностно-статистические методы и методы теории нечеткости обычно рассматриваются как различные.

Для знакомства со спецификой нечетких множеств рассмотрим некоторые их свойства.

В дальнейшем считаем, что все рассматриваемые нечеткие множества являются подмножествами одного и того же множества .

Законы де Моргана для нечетких множеств. Как известно, законами де Моргана называются следующие тождества алгебры множеств

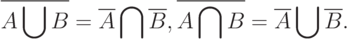$\overline{A\bigcup B}=\overline{A}\bigcap\overline{B},\overline{A\bigcap B}=\overline{A}\bigcup\overline{B}.$

( 2)

Теорема 1. Для нечетких множеств справедливы тождества

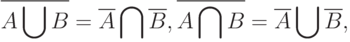$\overline{A\bigcup B}=\overline{A}\bigcap\overline{B},\overline{A\bigcap B}=\overline{A}\bigcup\overline{B},$

( 3)

$\overline{A+B}=\overline{A}\overline{B},\overline{AB}=\overline{A}+\overline{B}.$

( 4)

Доказательство теоремы 1 состоит в непосредственной проверке справедливости соотношений (3) и (4) путем вычисления значений функций принадлежности участвующих в этих соотношениях нечетких множеств на основе определений, данных выше.

Тождества (3) и (4) назовем законами де Моргана для нечетких множеств. В отличие от классического случая соотношений (2), они состоят из четырех тождеств, одна пара которых относится к операциям объединения и пересечения, а вторая - к операциям произведения и суммы. Как и соотношение (2) в алгебре множеств, законы де Моргана в алгебре нечетких множеств позволяют преобразовывать выражения и формулы, в состав которых входят операции отрицания.

Дистрибутивный закон для нечетких множеств. Некоторые свойства операций над множествами не выполнены для нечетких множеств. Так, 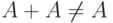$A+A\ne A$ за исключением случая, когда - "четкое" множество (т.е. функция принадлежности принимает только значения 0 и 1).

Верен ли дистрибутивный закон для нечетких множеств? В литературе иногда расплывчато утверждается, что "не всегда". Внесем полную ясность.

Теорема 2. Для любых нечетких множеств , 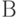и

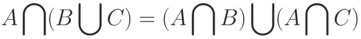$A\bigcap(B\bigcup C)=(A\bigcap B)\bigcup(A\bigcap C)$

( 5)

В то же время равенство

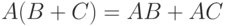( 6)

справедливо тогда и только тогда, когда при всех $y\in Y$

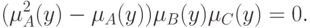
$(\mu_A^2(y)-\mu_A(y))\mu_B(y)\mu_C(y)=0.$

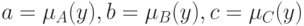Доказательство. Фиксируем произвольный элемент $y\in Y$ . Для сокращения записи обозначим $a=\mu_A(y),b=\mu_B(y),c=\mu_C(y)$ Для доказательства тождества (5) необходимо показать, что

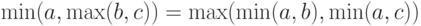$\min(a,\max(b,c))=\max(\min(a,b),\min(a,c))$

( 7)

Рассмотрим различные упорядочения трех чисел 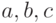a, b, c . Пусть сначала 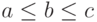$a\leq b\leq c$ . Тогда левая часть соотношения (7) есть 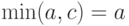$\min(a,c)=a$ , а правая $\max(a,a)=a$ , т.е. равенство (7) справедливо.

Пусть 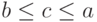$b\leq c\leq a$ . Тогда в соотношении (7) слева стоит 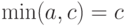$\min(a,c)=c$ , а справа 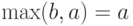$\max(b,a)=a$ , т.е. соотношение (7) опять является равенством.

Если 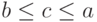$b\leq c\leq a$ , то в соотношении (7) слева стоит 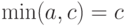$\min(a,c)=c$ , а справа 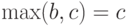$\max(b,c)=c$ , т.е. обе части снова совпадают.

Три остальные упорядочения чисел 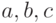a, b, c разбирать нет необходимости, поскольку в соотношение (6) числа и входят симметрично. Тождество (5) доказано.

Второе утверждение теоремы 2 вытекает из того, что в соответствии с определениями операций над нечеткими множествами

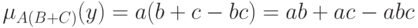
$\mu_{A(B+C)}(y)=a(b+c-bc)=ab+ac-abc$

и

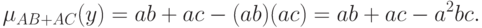
$\mu_{AB+AC}(y)=ab+ac-(ab)(ac)=ab+ac-a^2bc.$

Эти два выражения совпадают тогда и только тогда, когда a^2bc = abc , что и требовалось доказать.

Определение 1. Носителем нечеткого множества называется совокупность всех точек $y\in Y$ , для которых $\mu_A(y)>0$ .

Следствие теоремы 2. Если носители нечетких множеств и совпадают с , то равенство (6) имеет место тогда и только тогда, когда - "четкое" (т.е. обычное, классическое, не нечеткое) множество.

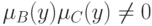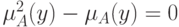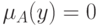Доказательство. По условию $\mu_B(y)\mu_C(y)\ne 0$ при всех $y\in Y$ . Тогда из теоремы 2 следует, что $\mu_A^2(y)-\mu_A(y)=0$ , т.е. $\mu_A(y)=1$ или $\mu_A(y)=0$ , что и означает, что - четкое множество.

Пример описания неопределенности с помощью нечеткого множества. Понятие "богатый" часто используется при обсуждении социально-экономических проблем, в том числе и в связи с подготовкой и принятием решений. Однако очевидно, что разные лица вкладывают в это понятие различное содержание. Сотрудники Института высоких статистических технологий и эконометрики провели в 2004 г. небольшое пилотное социологическое исследование представления различных слоев населения о понятии "богатый человек".

Мини-анкета опроса выглядела так:

При каком месячном доходе (в тыс. руб. на одного человека) Вы считали бы себя богатым человеком?
Оценив свой сегодняшний доход, к какой из категорий Вы себя относите:
a) богатые;

б) достаток выше среднего;

в) достаток ниже среднего;

г) бедные;

д) за чертой бедности.

(В дальнейшем вместо полного наименования категорий будем оперировать буквами, например "в" - категория, "б" - категория и т.д.)
Ваша профессия, специальность.

Дальше >>

Авторизоваться

Прикладная статистика

Различные виды статистических данных

1.4. Нечеткие множества - частный случай нечисловых данных

Вопросы и ответы