|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Различные виды статистических данных
1.3. Нечисловые данные
Статистика нечисловых данных - это направление в прикладной статистике, в котором в качестве исходных статистических данных (результатов наблюдений) рассматриваются объекты нечисловой природы. Так принято называть объекты, которые нельзя складывать и умножать на числа, в частности, элементы нелинейных пространств. Примерами являются бинарные отношения (ранжировки, разбиения, толерантности и др.), результаты парных и множественных сравнений, множества, нечеткие множества, измерение в шкалах, отличных от абсолютных. Этот перечень примеров не претендует на законченность. Он складывался постепенно, по мере того, как развивались теоретические исследования в области статистики нечисловых данных и расширялся опыт применений этого направления прикладной статистики.
Объекты нечисловой природы широко используются в теоретических и прикладных исследованиях по экономике, менеджменту и другим проблемам управления, в частности, управления качеством продукции, в технических науках, социологии, психологии, медицине и т.д., а также практически во всех отраслях народного хозяйства.
Начнем с первоначального знакомства с основными видами объектов нечисловой природы.
Результаты измерений в шкалах, отличных от абсолютной. Рассмотрим более подробно конкретное исследование в области маркетинга образовательных услуг, послужившее поводом к развитию отечественных исследований по теории измерений. При изучении привлекательности различных профессий для выпускников новосибирских школ был составлен список из 30 профессий. Опрашиваемых просили оценить каждую из этих профессий одним из баллов 1,2,...,10 по правилу: чем больше нравится, тем выше балл. Для получения социологических выводов необходимо было дать единую оценку привлекательности определенной профессии для совокупности выпускников школ. В качестве такой оценки в работе [ [ 1.24 ] ] использовалось среднее арифметическое баллов, выставленных профессии опрошенными школьниками. В частности, физика получила средний балл 7,69, а математика - 7,50. Поскольку 7,69 больше, чем 7,50, был сделан вывод, что физика более предпочтительна для школьников, чем математика.
Однако этот вывод противоречит данным работы [ [ 1.25 ] ], согласно которым ленинградские школьники средних классов больше любят математику, чем физику. Обсудим одно из возможных объяснений этого противоречия, которое сводится к указанию на неадекватность (с точки зрения теории измерений) методики обработки эконометрических данных, примененной в работе [ [ 1.24 ] ].
Дело в том, что баллы 1,2,...,10 введены конкретными исследователями, т.е. субъективно. Если одна профессия оценена в 10 баллов, а вторая - в 2, то из этого нельзя заключить, что первая ровно в 5 раз привлекательней второй. Другой коллектив социологов мог бы принять иную систему баллов, например 1,4,9,16,...,100. Естественно предположить, что упорядочивание профессий по привлекательности, присущее школьникам, не зависит от того, какой системой баллов им предложит пользоваться маркетолог.
Раз так, то распределение профессий по градациям десятибалльной системы не изменится, если перейти к другой системе баллов с помощью любого допустимого преобразования в порядковой шкале, т.е. с помощью строго возрастающей функции 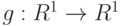 . Если
. Если 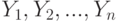 - ответы
- ответы  выпускников школ, касающихся математики, а
выпускников школ, касающихся математики, а  - физики, то после перехода к новой системе баллов ответы относительно математики будут иметь вид
- физики, то после перехода к новой системе баллов ответы относительно математики будут иметь вид 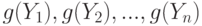 , а относительно физики -
, а относительно физики - 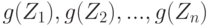 .
.
Пусть единая оценка привлекательности профессии вычисляется с помощью функции  . Какие требования естественно наложить на функцию
. Какие требования естественно наложить на функцию  , чтобы полученные с ее помощью выводы не зависели от того, какой именно системой баллов пользовался специалист по маркетингу образовательных услуг?
, чтобы полученные с ее помощью выводы не зависели от того, какой именно системой баллов пользовался специалист по маркетингу образовательных услуг?
Замечание. Обсуждение можно вести в терминах экспертных оценок. Тогда вместо сравнения математики и физики  экспертов (а не выпускников школ) оценивают по конкурентоспособности на мировом рынке, например, две марки стали. Однако в настоящее время маркетинговые и социологические исследования более привычны, чем экспертные.
экспертов (а не выпускников школ) оценивают по конкурентоспособности на мировом рынке, например, две марки стали. Однако в настоящее время маркетинговые и социологические исследования более привычны, чем экспертные.
Единая оценка вычислялась для того, чтобы сравнивать профессии по привлекательности. Пусть  - среднее по Коши. Пусть среднее по первой совокупности меньше среднего по второй совокупности:
- среднее по Коши. Пусть среднее по первой совокупности меньше среднего по второй совокупности:

Тогда согласно теории измерений необходимо потребовать, чтобы для любого допустимого преобразования  из группы допустимых преобразований в порядковой шкале было справедливо также неравенство
из группы допустимых преобразований в порядковой шкале было справедливо также неравенство
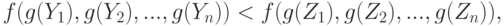
т.е. среднее преобразованных значений из первой совокупности также было меньше среднего преобразованных значений для второй совокупности. Причем сформулированное условие должно быть верно для любых двух совокупностей 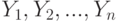 и
и  и, напомним, любого допустимого преобразования. Средние величины, удовлетворяющие сформулированному условию, называют допустимыми (в порядковой шкале). Согласно теории измерений только такими средними можно пользоваться при анализе мнений выпускников школ, экспертов и иных данных, измеренных в порядковой шкале.
и, напомним, любого допустимого преобразования. Средние величины, удовлетворяющие сформулированному условию, называют допустимыми (в порядковой шкале). Согласно теории измерений только такими средними можно пользоваться при анализе мнений выпускников школ, экспертов и иных данных, измеренных в порядковой шкале.
Какие единые оценки привлекательности профессий  устойчивы относительно сравнения? Ответ на этот вопрос дается ниже в
"Описание данных"
. В частности, оказалось, что средним арифметическим, как в работе [
[
1.24
]
] новосибирских специалистов по маркетингу образовательных услуг, пользоваться нельзя, а порядковыми статистиками, т.е. членами вариационного ряда (и только ими) - можно.
устойчивы относительно сравнения? Ответ на этот вопрос дается ниже в
"Описание данных"
. В частности, оказалось, что средним арифметическим, как в работе [
[
1.24
]
] новосибирских специалистов по маркетингу образовательных услуг, пользоваться нельзя, а порядковыми статистиками, т.е. членами вариационного ряда (и только ими) - можно.
Методы анализа конкретных экономических данных, измеренных в шкалах, отличных от абсолютной, являются предметом изучения в статистике нечисловых данных как части прикладной статистики. Как известно, основные шкалы измерения делятся на качественные (шкалы наименований и порядка) и количественные (шкалы интервалов, отношений, разностей, абсолютная). Методы анализа статистических данных в количественных шкалах сравнительно мало отличаются от таковых в абсолютной шкале. Добавляется только требование инвариантности относительно преобразований сдвига и/или масштаба. Методы анализа качественных данных - принципиально иные.
Напомним, что исходным понятием теории измерений является совокупность  допустимых преобразований шкалы (обычно
допустимых преобразований шкалы (обычно  - группа),
- группа),  . Алгоритм обработки данных
. Алгоритм обработки данных  , т.е. функция
, т.е. функция  (здесь
(здесь  -множество возможных результатов работы алгоритма) называется адекватным в шкале с совокупностью допустимых преобразований
-множество возможных результатов работы алгоритма) называется адекватным в шкале с совокупностью допустимых преобразований  , если
, если
 |
( 1) |
для всех 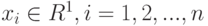 и всех
и всех  . Таким образом, теорию измерений рассматриваем как теорию инвариантов относительно различных совокупностей допустимых преобразований
. Таким образом, теорию измерений рассматриваем как теорию инвариантов относительно различных совокупностей допустимых преобразований  . Интерес вызывают две задачи:
. Интерес вызывают две задачи:
- дана группа допустимых преобразований
 (т.е. задана шкала). Какие алгоритмы анализа данных
(т.е. задана шкала). Какие алгоритмы анализа данных  из определенного класса являются адекватными?
из определенного класса являются адекватными? - дан алгоритм анализа данных
 . Для каких шкал (т.е. групп допустимых преобразований
. Для каких шкал (т.е. групп допустимых преобразований  ) он является адекватным?
) он является адекватным?
В "Описание данных" первая задача рассматривается для алгоритмов расчета средних величин. Информацию о других результатах решения задач указанных типов можно найти в работах [ [ 1.15 ] , [ 1.19 ] , [ 1.20 ] ].
Бинарные отношения. Пусть 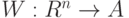 - адекватный алгоритм в шкале наименований. Можно показать, что этот алгоритм задается некоторой функцией от матрицы
- адекватный алгоритм в шкале наименований. Можно показать, что этот алгоритм задается некоторой функцией от матрицы  где
где
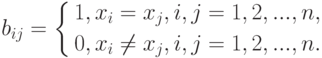
Если 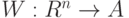 - адекватный алгоритм в порядковой шкале, то этот алгоритм задается некоторой функцией от матрицы
- адекватный алгоритм в порядковой шкале, то этот алгоритм задается некоторой функцией от матрицы  порядка
порядка  , где
, где
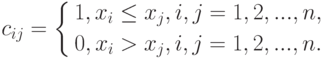
Матрицы  и
и  можно проинтерпретировать в терминах бинарных отношений. Пусть некоторая характеристика измеряется у
можно проинтерпретировать в терминах бинарных отношений. Пусть некоторая характеристика измеряется у  объектов
объектов 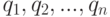 , причем
, причем  - результат ее измерения у объекта
- результат ее измерения у объекта  . Тогда матрицы
. Тогда матрицы  и
и  задают бинарные отношения на множестве объектов
задают бинарные отношения на множестве объектов  . Поскольку бинарное отношение можно рассматривать как подмножество декартова квадрата
. Поскольку бинарное отношение можно рассматривать как подмножество декартова квадрата  , то любой матрице
, то любой матрице  порядка
порядка  из 0 и 1 соответствует бинарное отношение
из 0 и 1 соответствует бинарное отношение 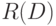 , определяемое следующим образом:
, определяемое следующим образом: 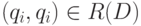 тогда и только тогда, когда
тогда и только тогда, когда 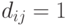 .
.
Бинарное отношение 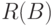 - отношение эквивалентности, т.е. симметричное рефлексивное транзитивное отношение. Оно задает разбиение
- отношение эквивалентности, т.е. симметричное рефлексивное транзитивное отношение. Оно задает разбиение  на классы эквивалентности. Два объекта
на классы эквивалентности. Два объекта  и
и 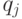 входят в один класс эквивалентности тогда и только тогда, когда
входят в один класс эквивалентности тогда и только тогда, когда  .
.
Выше показано, как разбиения возникают в результате измерений в шкале наименований. Разбиения могут появляться и непосредственно. Так, при оценке качества промышленной продукции эксперты дают разбиение показателей качества на группы. Для изучения психологического состояния людей их просят разбить предъявленные рисунки на группы сходных между собой. Аналогичная методика применяется и в иных экспериментальных психологических исследованиях, необходимых для оптимизации управления персоналом.
Во многих эконометрических задачах разбиения получаются "на выходе" (например, в кластерном анализе) или же используются на промежуточных этапах анализа данных (например, сначала проводят классификацию с целью выделения однородных групп, а затем в каждой группе строят регрессионную зависимость).
Бинарное отношение 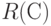 задает разбиение
задает разбиение  на классы эквивалентности, между которыми введено отношение строгого порядка. Два объекта
на классы эквивалентности, между которыми введено отношение строгого порядка. Два объекта  и
и 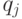 входят в один класс тогда и только тогда, когда
входят в один класс тогда и только тогда, когда 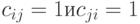 , т.е.
, т.е.  . Класс эквивалентности
. Класс эквивалентности 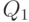 предшествует классу эквивалентности
предшествует классу эквивалентности 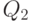 тогда и только тогда, когда для любых
тогда и только тогда, когда для любых  имеем
имеем 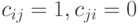 , т.е.
, т.е.  . Такое бинарное отношение в статистике часто называют ранжировкой со связями; связанными считаются объекты, входящие в один класс эквивалентности. В литературе встречаются и другие названия: линейный квазипорядок, упорядочение, квазисерия, ранжирование. Если каждый из классов эквивалентности состоит только из одного элемента, то имеем обычную ранжировку (другими словами, линейный порядок).
. Такое бинарное отношение в статистике часто называют ранжировкой со связями; связанными считаются объекты, входящие в один класс эквивалентности. В литературе встречаются и другие названия: линейный квазипорядок, упорядочение, квазисерия, ранжирование. Если каждый из классов эквивалентности состоит только из одного элемента, то имеем обычную ранжировку (другими словами, линейный порядок).
Как известно, ранжировки возникают в результате измерений в порядковой шкале. Так, при описанном выше опросе ответ выпускника школы - это ранжировка (со связями) профессий по привлекательности. Ранжировки часто возникают и непосредственно, без промежуточного этапа - приписывания объектам квазичисловых оценок - баллов. Многочисленные примеры тому приведены английским статистиком М. Кендэлом [ [ 1.8 ] ]. При оценке качества промышленной продукции широко применяемые нормативные и методические документы предусматривают использование ранжировок.
Для прикладных областей, кроме ранжировок и разбиений, представляют интерес толерантности, т.е. рефлексивные симметричные отношения. Толерантность - математическая модель для выражения представлений о сходстве (похожести, близости). Разбиения - частный вид толерантностей. Толерантность, обладающая свойством транзитивности - это разбиение. Однако в общем случае толерантность не обязана быть транзитивной. Толерантности появляются во многих постановках теории экспертных оценок, например, как результат парных сравнений (см. ниже).
Напомним, что любое бинарное отношение на конечном множестве может быть описано матрицей из 0 и 1.
Дихотомические (бинарные) данные. Это данные, которые могут принимать одно из двух значений (0 или 1), т.е. результаты измерений значений альтернативного признака. Как уже было показано, измерения в шкале наименований и порядковой шкале приводят к бинарным отношениям, а те могут быть выражены, как результаты измерений по нескольким альтернативным признакам, соответствующим элементам матриц, описывающих отношения. Дихотомические данные возникают в прикладных исследованиях и многими иными путями.
В настоящее время в большинстве стандартов, технических условий, технических регламентов, договоров на поставку конкретной продукции предусмотрен контроль по альтернативному признаку. Это означает, что единица продукции относится к одной из двух категорий - "годных" или "дефектных", т.е. соответствующих или не соответствующих требованиям стандарта. Отечественными специалистами проведены обширные теоретические исследования проблем статистического приемочного контроля по альтернативному признаку. Основополагающими в этой области являются работы академика А.Н. Колмогорова. Подход советской вероятностно-статистической школы к проблемам контроля качества продукции отражен в монографиях [ [ 1.1 ] , [ 1.10 ] ] (см. также "Различные виды статистических данных" ).
Дихотомические данные - давний объект прикладной статистики. Особенно большое применение они имеют в экономических и социологических исследованиях, в которых большинство переменных, интересующих специалистов, измеряется по качественным шкалам. При этом дихотомические данные зачастую являются более адекватными, чем результаты измерений по методикам, использующим большее число градаций. В частности, психологические тесты типа MMPI используют только дихотомические данные. На них опираются и популярные в технико-экономическом анализе методы парных сравнений [ [ 1.5 ] ].
Элементарным актом в методе парных сравнений является предъявление эксперту для сравнения двух объектов (сравнение может проводиться также прибором). В одних постановках эксперт должен выбрать из двух объектов лучший по качеству, в других - ответить, похожи объекты или нет. В обоих случаях ответ эксперта можно выразить одной из двух цифр (меток) - 0 или 1. В первой постановке: 0, если лучшим объявлен первый объект; 1 - если второй. Во второй постановке: 0, если объекты похожи, схожи, близки; 1 - в противном случае.
Подводя итоги изложенному, можно сказать, что рассмотренные выше данные представимы в виде векторов из 0 и 1 (при этом матрицы, очевидно, могут быть записаны в виде векторов). Поскольку все результаты наблюдений имеют лишь несколько значащих цифр, то, используя двоичную систему счисления, любые виды анализируемых статистическими методами данных можно записать в виде векторов конечной длины (размерности) из 0 и 1. Представляется, что эта возможность в большинстве случаев имеет лишь академический интерес, но во всяком случае можно констатировать, что анализ дихотомических данных необходим во многих прикладных постановках.
Множества. Совокупность 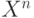 векторов
векторов 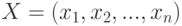 из 0 и 1 размерности
из 0 и 1 размерности  находится во взаимнооднозначном соответствии с совокупностью из
находится во взаимнооднозначном соответствии с совокупностью из  всех подмножеств множества
всех подмножеств множества  . При этом вектору
. При этом вектору 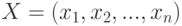 соответствует подмножество
соответствует подмножество  , состоящее из тех и только из тех
, состоящее из тех и только из тех  , для которых
, для которых 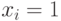 . Это объясняет, почему изложение вероятностных и статистических результатов, относящихся к анализу данных, являющихся объектами нечисловой природы перечисленных выше видов, можно вести на языке конечных случайных множеств, как это было сделано в монографии [
[
1.15
]
].
. Это объясняет, почему изложение вероятностных и статистических результатов, относящихся к анализу данных, являющихся объектами нечисловой природы перечисленных выше видов, можно вести на языке конечных случайных множеств, как это было сделано в монографии [
[
1.15
]
].
Множества как исходные данные появляются и в иных постановках. Из геологических задач исходил Ж. Матерон, из электротехнических - Н.Н. Ляшенко и др. Случайные множества применялись для описания процесса случайного распространения, например, распространения информации, слухов, эпидемии или пожара, а также в математической экономике. В монографии [ [ 1.15 ] ] рассмотрены приложения случайных множеств в теории экспертных оценок и в теории управления запасами и ресурсами (логистике).
Отметим, что с точки зрения математики реальные объекты можно моделировать случайными множествами как из конечного числа элементов, так и из бесконечного, однако при расчетах на компьютерах неизбежна дискретизация, т.е. переход к первой из названных возможностей.
