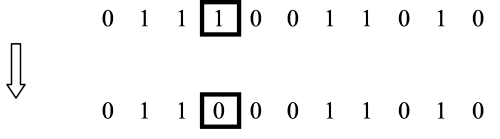Модификации генетических алгоритмов
3.4 Оператор мутации
После выполнения операторов рекомбинации (скрещивания) полученные потомки с вероятностью 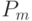 подвергаются мутации, которая может быть выполнена различными способами.
подвергаются мутации, которая может быть выполнена различными способами.
3.4.1 Двоичная мутация
3.4.1.1 Классическая мутация
Этот вид оператора уже рассматривался в простом ГА. Здесь для каждой особи случайно выбирается позиция и с малой вероятностью (от 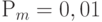 до
до  ) выполняется инвертирование значения переменной в выбранной позиции. Пример выполнения этого оператора представлен на рис.3.17.
) выполняется инвертирование значения переменной в выбранной позиции. Пример выполнения этого оператора представлен на рис.3.17.
3.4.1.2 Оператор инверсии
Иногда используется следующий оператор инверсии, фактически являющийся разновидностью мутации. При этом случайным образом выбираются две позиции в особи и далее производится обмен значениями генов между ними. Пример выполнения этого оператора представлен на рис.3.18.
3.4.2 Мутация над вещественными числами
Мутация над вещественными потомками выполняется путем сложения особи с небольшим случайным значением, которое называется шагом мутации. Выбор размера шага мутации зависит от рассматриваемой проблемы, и шаг в общем случае может изменяться в процессе решения задачи. Маленький шаг дает большую точность, но ведет к большим временным затратам. Мутация с постоянным шагом и постоянной вероятностью называется однородной.
Оператор мутации над вещественным числом выполняется следующим образом
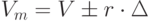 |
( 3.7) |
где 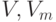 – значения вещественной переменной до и после мутации;
– значения вещественной переменной до и после мутации;
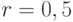 (диапазон изменения переменной) и
(диапазон изменения переменной) и  - случайное число от 0 до 1
- случайное число от 0 до 1
Часто для повышения эффективности поиска вероятность мутации и шаг изменяются в процессе решения задачи.
Рассмотрим далее способы изменения вероятности мутации. Мутация с равной вероятностью может привести как к увеличению, так и к уменьшению значения целевой функции. На этапе сходимости ГА к оптимуму целесообразно уменьшать вероятность случайной мутации. Обычно на начальном этапе  , а на конечном этапе вероятность мутации уменьшают. Для реализации этой процедуры иногда используют метод моделирования отжига (simulation annealing), который дает следующий закон изменения вероятности мутации:
, а на конечном этапе вероятность мутации уменьшают. Для реализации этой процедуры иногда используют метод моделирования отжига (simulation annealing), который дает следующий закон изменения вероятности мутации:
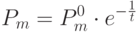 |
( 3.8) |
где  – номер поколения.
– номер поколения.
Здесь изменяется шаг мутации. Вначале шаг мутации имеет достаточно большое значение, которое далее постепенно уменьшается. Рассмотрим этот тип оператора для векторного случая
![\begin{array}{cl}S_v^t=\langle V_1,V_2,\dots ,V_k,\dots V_m\rangle\\V_k\in[l_k,U_k]\end{array}](/sites/default/files/tex_cache/821fecd0dbca3d96398c91d20df221e0.png)
В результате выполнения мутации получаем следующий вектор (особь популяции)
![\begin{array}{cl}S_v^{t+1}=\langle V_1,V_2,\dots ,V'_k,\dots V_m\rangle\\k\in[1,\dots n]\end{array}](/sites/default/files/tex_cache/cc0b37232818bb567cf276ce01780e98.png) |
( 3.9) |
где компонента вектора вычисляется следуюшим образом
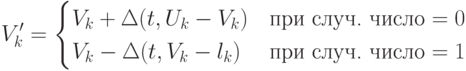 |
( 3.10) |
где ![\Delta(t,y)\in[0,y]](/sites/default/files/tex_cache/b4bbf3d6e0e53f8ff568f1b07642f6a9.png) и
и 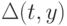 определяет шаг мутации, который с увеличением номера поколения
определяет шаг мутации, который с увеличением номера поколения  уменьшается:
уменьшается:
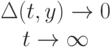
Один из вариантов реализации функции, определяющей шаг 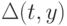 ,следующий:
,следующий:
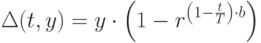 |
( 3.11) |
где ![r\in[1,\dots n]](/sites/default/files/tex_cache/a3bba70fad2ac7bcb1f87d383774116d.png) (
( -случайное число) и
-случайное число) и  – максимальное число поколений;
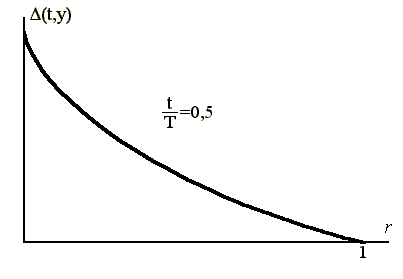
– максимальное число поколений; 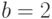 – параметр, определяющий степень неоднородности. На рис.3.19 показан для наглядности график изменения шага мутации, который в пределе стремится к 0.
– параметр, определяющий степень неоднородности. На рис.3.19 показан для наглядности график изменения шага мутации, который в пределе стремится к 0.