Модификации генетических алгоритмов

3.9. Ниши в генетических алгоритмах

Для мультимодальных функций, которые имеют много экстремумов, часто представляет интерес найти не одно, а несколько экстремальных значений. С помощью стандартного ГА это трудно сделать, поскольку в процессе эволюции, как правило, благодаря "генетическому дрейфу" особи концентрируются в окрестности одного экстремума. Поэтому для поиска экстремумов мультимодальных функций были разработаны соответствующие методы.

Простейший из них основан на многократном запуске ГА на различных подмножествах пространства поиска решений. Показано [6], что, если все экстремумы имеют примерно одинаковую небольшую вероятность поиска (быть найденными), то число независимых запусков ГА должно быть

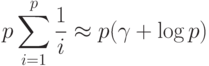( 3.16)

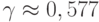где – число экстремумов и - константа Эйлера. К сожалению, в большинстве реальных задач экстремумы не являются равновероятными и поэтому число запусков должно быть больше приведенной оценки. Возможна также параллельная реализация этого итеративного метода.

В [6] предложен наиболее известный метод для данной проблематики, который основан на разделении популяции на несколько подпопуляций. Основная идея состоит в том, что фитнесс-функция модифицируется таким образом, чтобы в случае, когда особи концентрируются вокруг экстремума, значение фитнесс-функции для них уменьшалось пропорционально числу особей в этой области. При этом модифицированное значение фитнесс-функци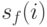и особи , называемое разделенной фитнесс-функцией, определяется следующим образом

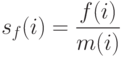( 3.17)

где 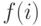– значение исходной фитнесс-функции и 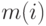называется счетчиком ниши. Для особи величина 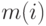вычисляется путем суммирования значений разделяющей функции 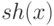для особей всей популяции:

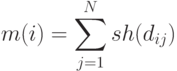( 3.18)

где 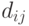- евклидово расстояние между двумя особями и . Разделяющая функция 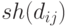должна обладать следующими свойствами:

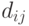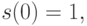
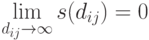( 3.19)

Одной из применяемых на практике функций, для которой эти условия выполняются, является следующая

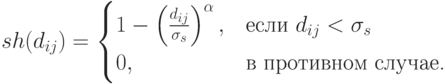( 3.20)

Здесь и 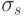являются константами. Наибольшие трудности в этом методе вызывает выбор значения 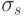, который требует априорного знания числа экстремумов функции, что, как правило, заранее неизвестно.

Например, в программе FlexTool [4] 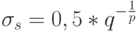, где полагается равным примерному числу экстремумов. Значение часто полагают равным 1, что означает одинаковую степень соучастия соседних особей. Таким образом, функция 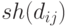определяет уровень близости и степень соучастия для каждой особи в популяции. Если особь находится в своей нише в одиночестве, то 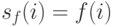. В противном случае значение модифицированной фиттнесс-функции уменьшается пропорционально количеству и степени близости соседствующих хромосом. При этом увеличение количества похожих друг на друга хромосом в одной нише ограничено, поскольку такое увеличение ведет к уменьшению значения фитнесс-функции таких особей.

Имеются различные модификации этого метода. Например, расстояние 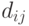между особями иногда определяются не на уровне фенотипа (евклидово расстояние), а на уровне генотипа, где используется расстояние Хэмминга между двоичными кодами хромосом.

В работе [4] приведено сравнение параллельных и последовательных методов обработки ниш. Параллельные методы формируют и сохраняют ниши одновременно с популяцией. Последовательные методы обрабатывают различные ниши в разные моменты времени. Как правило, по эффективности параллельные методы превосходят последовательные.