Эволюционные вычисления
[+]
Московский государственный университет путей сообщения
Опубликован: 10.10.2014 | Доступ: свободный | Студентов: 866 / 193 | Длительность: 22:10:00
Тема: Алгоритмы и дискретные структуры
Специальности: Программист, Архитектор программного обеспечения
Лекция 2:

Генетические алгоритмы для задач комбинаторной оптимизации

A
|
версия для печати
< Лекция 1 || Лекция 2: 1234567 || Лекция 3 >
Аннотация: До сих пор рассматривалось применение ГА, в основном, при решении задачи численной оптимизации при поиске экстремумов функции. Но в настоящее время ГА используются больше для решения задач комбинаторной оптимизации, которым посвящена подавляющая часть публикаций. Базовой задачей комбинаторной оптимизации является задача коммивояжера, для которой отрабатываются новые методы решения задач данного типа. Поэтому большая часть лекции посвящена решению задачи коммивояжера с помощью ГА на основе различных способов кодирования потенциальных решений и проблемно-ориентированных генетических операторов кроссинговера. Однако сначала рассматриваются задачи об укладке рюкзака и покрытии множества, которые допускают использование простого (классического) ГА.
Ключевые слова: стоимость, целое число, постановка задачи, множества, вектор, задача об укладке рюкзака, подмножество, путь, Ориентированный граф, гамильтонов, информация, вес, расстояние, перестановка, размерность, NP, комбинаторная оптимизация, представление, проблемно-ориентированные генетические операторы, операторы, задача коммивояжера, кодирование потенциальных решений

2.1. Задача об укладке рюкзака

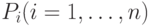Эта задача имеет следующую неформальную простую постановку [4,5]. Имеется рюкзак объемом C и n различных предметов. Каждый предмет i имеет известный объем W_i и стоимость P_i(i=1,\dots,n). В рюкзак можно положить целое число различных предметов. Нужно упаковать рюкзак так, чтобы полная стоимость уложенных предметов была максимальной, а их общий объем не превышал заданный объем C. Форма предметов здесь не учитывается.

Формальная постановка задачи: для данного множества весов W_i, стоимостей P_i и объема C надо найти двоичный вектор

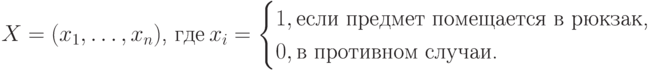
X=(x_1,\dots,x_n)\mbox{, где}\ x_i=\begin{cases}1,\mbox{если предмет помещается в рюкзак,}\\0,\mbox{в противном случаи.}\end{cases}

и при этом должно выполняться условие:

V=\sum_{i=1}^n W_i\le C\mbox{ и }\sum_{i=1}^n P_i=\max

Так как решение задачи можно представить двоичным вектором X= (x_1,\dots, x_n), то очевидно при его поиске можно применить простой ГА со стандартными операторами скрещивания и мутации. Но при этом на каждом шаге итерации надо следить за тем, чтобы новые решения, полученные в результате скрещивания или мутации, удовлетворяли требуемому ограничению V\le C. В случае невыполнения ограничения "неправильное" потенциальное решение должно быть уничтожено, что ведет к сокращению популяции.

В качестве фитнесс-функции в простейшем случае можно взять

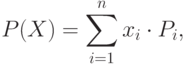
P(X)=\sum_{i=1}^n x_i\cdot P_i,
но в этом случае, как указано выше, есть проблемы с неправильными решениями.

Данная задача относится к классу задач с ограничениями, при решении которых применяются следующие подходы [4,5]: 1) введение в фитнесс-функцию дополнительного штрафа; 2) использование алгоритмов "восстановления" некорректных решений.

  1. В первом случае в фитнесс-функцию вводится дополнительная штрафная функция, которая для неправильных решений дает большие отрицательные значения ЦФ. При этом задача с ограничениями трансформируется в задачу без ограничений путем назначения штрафа для некорректных решений. Фитнесс-функция для каждой особи может быть определена следующим образом
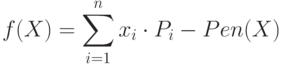
    f(X)=\sum_{i=1}^n x_i\cdot P_i-Pen(X)

    Разработано множество методов назначения штрафных значений, из которых ниже рассмотрено только три вида, когда рост значения штрафной функции относительно степени нарушения ограничения имеет логарифмический, линейный и квадратичный характер:

    • Pen(X)=\log_2(1+\rho\cdot(\sum_{i=1}^n x_i\cdot W_i-C)),
    • Pen(X)=\rho\cdot(\sum_{i=1}^n x_i\cdot W_i-C),
    • Pen(X)=(\rho\cdot(\sum_{i=1}^n x_i\cdot W_i-C))^2.

    Здесь для всех трех случаев \rho = \max_{1 \le i \le n} {P_i/w_i}.

  2. Второй подход к решению задач с ограничениями основан на специальных алгоритмах "восстановления" некорректных решений. Следует отметить, что многие алгоритмы восстановления требуют значительных вычислительных ресурсов, и полученные решения иногда требуют адаптации к конкретным практическим приложениям.

    В этом случае в качестве фитнесс-функции используется

    f(X')=\sum_{i=1}^n x_i'P_i,
    где вектор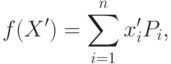 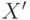X'– восстановленная версия исходного вектора X. Здесь следует отметить, по крайней мере, два аспекта. Во-первых, можно использовать различные алгоритмы восстановления. Во-вторых, восстановленные особи могут замещать только некоторую часть исходных особей в популяции. Процент замещаемых особей может варьироваться от 0% до 100% и его значение является важнейшим параметром метода восстановления. В некоторых работах отмечается, что наилучшие результаты получаются при 5%, во всяком случае, лучше, чем в двух крайних случаях – 0% (без замещения) и 100% (любая восстановленная особь заменяет исходную). Ниже приведен простой алгоритм восстановления.


    При этом используются два основных способа выбора объекта:

    • случайный выбор объекта из рюкзака;
    • "жадное восстановление", при котором вначале все предметы сортируются в порядке убывания их стоимости P_i и на каждом шаге для удаления выбирается предмет минимальной стоимости (из имеющихся в рюкзаке).

  3. Третий подход к решению задач с ограничениями использует специальное отображение (декодирование) особей, которое гарантирует генерацию допустимого решения (с учетом ограничений), или используют проблемно-ориентированные генетические операторы, сохраняющие корректность решения.

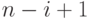    Рассмотрим один из возможных вариантов алгоритма декодирования, который основан на кодировании решения вектором целых чисел, так называемом "упорядоченном представлении" (ordinal representation), подробно описанном в разделе 3.3.2. Здесь каждая хромосома кодируется вектором e целых чисел, где i-я компонента вектора – есть целое число в диапазоне от 1 до n-i+1. "Упорядоченное представление" использует для ссылок (базовый) список предметов L. Вектор e фактически содержит указатели на базовый список L. Декодирование вектора осуществляется путем выбора соответствующего предмета из текущего списка и удаления его из базового списка. 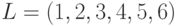Например, при базовом списке предметов L=(1,2,3,4,5,6) текущий вектор 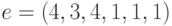e=(4,3,4,1,1,1) декодируется в следующую последовательность предметов: 4, 3, 6, 1,2, 5. Первым в рюкзак включается четвертый элемент списка L- 4, который устраняется из L. Далее в рюкзак включается третий элемент из текущего списка L. Затем включается 6 - четвертый элемент текущего L и т.д. Подробнее описание этого представления и выполнение кроссинговера на нем описано в разделе 2.3.2. В данном методе хромосома может интерпретироваться как стратегия (порядок) включения предметов в решение. Отметим, что основным достоинством данного кодирования хромосомы является то, что на нем работает одноточечный кроссинговер. То есть для двух допустимых решений –родителей кроссинговер порождает также допустимое решение–потомок. Оператор мутации при данном представлении выполняется путем замены i-го гена (целочисленной компоненты вектора) на случайное целое число из диапазона [1,\dots,n-i+1].


    Очевидно, что представленный алгоритм зависит от способа генерации списка предметов L. Обычно используются два метода генерации этого списка:

    • список предметов L генерируется в том порядке, в котором предметы расположены во входном файле (как правило, случайно
    • список предметов L генерируется в порядке убывания их стоимостей (жадный алгоритм). Декодирование вектора X выполняется на основе отсортированного вектора. Например, x_{25} интерпретируется как 25-й предмет текущего списка L

Задача об укладке рюкзака в различных вариантах имеет многочисленные практические приложения. Например, к ней можно свести оптимизацию загрузки транспорта и т.п.

Дальше >>
< Лекция 1 || Лекция 2: 1234567 || Лекция 3 >

Вопросы и ответы

вопросов: 0