Генетические алгоритмы для задач комбинаторной оптимизации
2.3.4.2. Матрица предшествования
Рассмотрим представление тура в виде двоичной матрицы предшествования [4]. В этом случае элемент матрицы  равен 1, если и только если город
равен 1, если и только если город  предшествует (встречается в туре раньше) городу
предшествует (встречается в туре раньше) городу  . В противном случае
. В противном случае 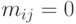 . Отметим, что здесь имеется в виду не только непосредственное предшествование (город
. Отметим, что здесь имеется в виду не только непосредственное предшествование (город  связан непосредственно с городом
связан непосредственно с городом  ) но и более "глубокое". Например, тур
) но и более "глубокое". Например, тур  =(3-1-2-8-7-4-6-9-5) представляется бинарной матрицей предшествования, которая показана в табл.2.5 Здесь элементы главной диагонали
=(3-1-2-8-7-4-6-9-5) представляется бинарной матрицей предшествования, которая показана в табл.2.5 Здесь элементы главной диагонали 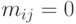 и
и 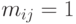 , если
, если  -й город предшествует в туре
-й город предшествует в туре  -му городу. Например, в первой строке город 1 предшествует в туре городам 2, 4, ….,9, но не предшествует городу 3.
-му городу. Например, в первой строке город 1 предшествует в туре городам 2, 4, ….,9, но не предшествует городу 3.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 3 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 4 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 7 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 |
| 8 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| 9 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
В этом представлении тура матрица  размерности
размерности  обладает следующими свойствами:
обладает следующими свойствами:
- число единиц в матрице равно точно
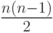 ;
; -
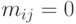 для всех
для всех 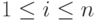 ;
; - если
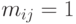 и
и 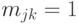 , то
, то  .
.
Если число единиц в матрице меньше чем 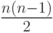 , а два других требования выполняются, то города частично упорядочены. Это означает, что можно получить матрицу (по крайней мере одним способом), которая представляет правильный тур. На этой форме представления вводятся два новых генетических оператора кроссинговера: пересечение и объединение.
, а два других требования выполняются, то города частично упорядочены. Это означает, что можно получить матрицу (по крайней мере одним способом), которая представляет правильный тур. На этой форме представления вводятся два новых генетических оператора кроссинговера: пересечение и объединение.
Оператор пересечения основан на том, что побитовое пересечение матриц дает матрицу, где:
- число единиц не больше
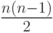 ;
; - выполняются два других требования.
Таким образом, можно получить матрицу, представляющую правильный тур. Например, для двух родителей  = (1-2-3-4-5-6-7-8-9) и
= (1-2-3-4-5-6-7-8-9) и  = (4-1-2-8-7-6-9-3-5), представляемых матрицами табл.2.6 и табл.2.7 соответственно, поэлементное пересечение этих матриц дает матрицу табл.2.8.
= (4-1-2-8-7-6-9-3-5), представляемых матрицами табл.2.6 и табл.2.7 соответственно, поэлементное пересечение этих матриц дает матрицу табл.2.8.
Частичный порядок городов определяемый матрицей табл.2.4 следующий:
Город 1 предшествует городам 2, 3, 5, 6, 7, 8, 9;
Город 2 предшествует городам 3, 5, 6, 7, 8, 9;
Город 3 предшествует 5;
Город 4 – 5, 6, 7, 8, 9
Города 6, 7, 8 предшествуют 9.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 3 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 4 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 5 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
На заключительном этапе выполнения этого оператора выбирается один из родителей и в промежуточную матрицу (полученную после пересечения) добавляются некоторые единицы (чтобы их число было равно 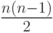 ) путем анализа сумм строк и столбцов, которые восстанавливают полный тур с учетом соответствующего родителя.
) путем анализа сумм строк и столбцов, которые восстанавливают полный тур с учетом соответствующего родителя.
В табл.2.8 для удобства показано число единиц по строкам и столбцам матрицы, которое, например, позволяет города разбить на подтуры или в некотором смысле эквивалентные группы. Анализ числа единиц в строках показывает, что тур должен начинаться с (1-2-4), остальные города можно разбить на группы (3,6,7,8) и (5,9). Анализ числа единиц по столбцам позволяет "выстроить" подтур (3-5-9), а для остальных трех городов можно выбрать, например, порядок (8-7-6). В результате получаем для потомка полный тур (1-2-4-8-7-6-3-5-9), который представлен матрицей табл.2.9, которая может быть получена из предыдущей табл.2.8.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 2 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 3 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 4 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |
| 7 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 8 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 9 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | N1 | |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 7 |
| 2 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 6 |
| 3 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 4 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 5 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| N1 | 0 | 1 | 2 | 0 | 4 | 3 | 3 | 3 | 6 |
Оператор объединения основан на том, что подмножество бит из одной матрицы может быть комбинировано с подмножеством бит из другой матрицы без потери свойства быть туром, если эти подмножества имеют пустое пересечение. Оператор разбивает множество городов на две непересекающиеся группы. При этом для первой группы городов копируются биты из первой матрицы, а для второй группы копируются биты из второй матрицы.
На заключительном этапе матрица достраивается путем анализа сумм для строк и столбцов аналогично операции пересечения. Например, два родителя  и
и  , которые представлены табл.2.6 и табл.2.7, и разбиения городов {1, 2, 3, 4,} и {5, 6, 7, 8, 9} порождают матрицу табл.2.10.
, которые представлены табл.2.6 и табл.2.7, и разбиения городов {1, 2, 3, 4,} и {5, 6, 7, 8, 9} порождают матрицу табл.2.10.
Таким образом, для решения задачи коммивояжера, в основном, используется не классическое двоичное представление, а более сложные списочные и матричные структуры, которых разработано достаточно много (каждый уважающий себя автор, как правило, предлагает свой способ кодирования потенциального решения и проблемно-ориентированные генетические операторы). Цель данного раздела, в первую очередь, заключалась в представлении некоторых нестандартных способов кодирования особей и проблемно-ориентированных генетических операторов. Подробнее данная проблема освещена в специальной литературе. В следующем разделе, где рассматриваются различные модификации генетических алгоритмов, фактически эта тема будет продолжена.
