Эволюционные вычисления
[+]
Московский государственный университет путей сообщения
Опубликован: 10.10.2014 | Доступ: свободный | Студентов: 869 / 193 | Длительность: 22:10:00
Тема: Алгоритмы и дискретные структуры
Специальности: Программист, Архитектор программного обеспечения
Лекция 2:

Генетические алгоритмы для задач комбинаторной оптимизации

A
|
версия для печати
< Лекция 1 || Лекция 2: 1234567 || Лекция 3 >

Контрольные вопросы

  1. При решении каких задач комбинаторной оптимизации может быть использован простой ГА с двоичным кодированием хромосом?
  2. Какие модификации необходимы для эффективного использования простого ГА для решения задачи укладки рюкзака?
  3. Какие виды штрафных функций могут быть использованы в фитнесс-функции при решении задачи укладки рюкзака?
  4. Выполните программную реализацию простого ГА на одном из языков программирования для решения задачи укладки рюкзака с введением в фитнесс-функцию штрафной функции. Исследуйте эффективность ГА в зависимости от вида штрафной функции.
  5. В чем суть алгоритма восстановления при решения задачи укладки рюкзака?
  6. Выполните программную реализацию простого ГА на одном из языков программирования для решения задачи укладки рюкзака с использованием алгоритма восстановления.
  7. Выполните программную реализацию простого ГА на одном из языков программирования для решения задачи укладки рюкзака с использованием алгоритма декодирования.
  8. Как может быть использован простой ГА с двоичным кодированием хромосом для решения задачи о покрытии?
  9. Почему неэффективно двоичное кодирование хромосомы при решении задачи коммивояжера?
  10. Опишите основные виды недвоичного представления хромосомы для задачи коммивояжера.
  11. Опишите "представление соседства" и проблемно-ориентированные операторы кроссинговера: обмен ребер, обмен туров, эвристический кроссинговер.
  12. Как может быть выполнен оператор мутации на представлении соседства?
  13. Опишите "упорядоченное представление" и укажите какой тип оператора кроссинговера может на нем использоваться.
  14. Опишите "представление путей" и проблемно-ориентированные операторы кроссинговера: частично соответствующей ОК (РМХ), упорядоченный ОК (ОХ), циклический ОК (СХ).
  15. Какие двоичные матрицы можно использовать для представления тура?
  16. Опишите соответствующие операторы кроссинговера для матрицы смежности.
  17. Чем отличается матрица предшествования от матрицы смежности и как можно реализовать операторы кроссинговера на ней?
  18. Придумайте свой способ кодирования (представления) полного тура для задачи коммивояжера и соответствующие генетические операторы.

Упражнения

  1. Реализовать с использованием генетических алгоритмов решение задачи коммивояжера по индивидуальному заданию согласно номеру варианта в табл.2.12
  2. Сравнить найденное решение с представленным в условии задачи оптимальным решением.
  3. Представить графически найденное решение.
  4. Проанализировать время выполнения и точность нахождения результата в зависимости от значений вероятностей различных видов кроссинговера мутации.
Таблица 2.12.
№ варианта Название функции Вид представления
1 Wi29.tsp Представление соседства
2 Dj89.tsp Представление соседства
3 Att48.tsp Представление соседства
4 Bayg29.tsp Представление соседства
5 Bayg29.tsp Представление соседства
6 Berlin52.tsp Представление соседства
7 Eil51.tsp Представление соседства
8 Eil76.tsp Представление соседства
9 Wi29.tsp Представление порядка
10 Dj89.tsp Представление порядка
11 Att48.tsp Представление порядка
12 Bayg29.tsp Представление порядка
13 Bayg29.tsp Представление порядка
14 Berlin52.tsp Представление порядка
15 Eil51.tsp Представление порядка
16 Eil76.tsp Представление порядка
17 Wi29.tsp Представление пути
18 Dj89.tsp Представление пути
19 Att48.tsp Представление пути
20 Bayg29.tsp Представление пути
21 Bayg29.tsp Представление пути
22 Berlin52.tsp Представление пути
23 Eil51.tsp Представление пути
24 Eil76.tsp Представление пути

Тестовые наборы (benchmarks) к упражнению представлены в трех формах:

  1. Эвклидовы координаты городов. Матрица расстояний получается путем нахождения эвклидовых расстояний между координатами города по формуле: 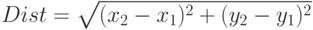Dist=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}. В случае эвклидовых координат городов они представлены в формате: №_города, координата x, координата y (через пробел).
  2. Полная матрица расстояний. Не обрабатывается, переписывается без изменений из файла.
  3. Диагональная матрица расстояний. Данную матрицу необходимо транспонировать, после чего заполнить верхнюю половину матрицы расстояний (от главной диагонали). Нижняя половина заполняется из верхней, с соблюдением условия Dist_{ij}=Dist_{ji}.
	Тип данных: эвклидовы координаты городов
1 20833.3333 17100.0000
2 20900.0000 17066.6667
3 21300.0000 13016.6667
4 21600.0000 14150.0000
5 21600.0000 14966.6667
6 21600.0000 16500.0000
7 22183.3333 13133.3333
8 22583.3333 14300.0000
9 22683.3333 12716.6667
10 23616.6667 15866.6667
11 23700.0000 15933.3333
12 23883.3333 14533.3333
13 24166.6667 13250.0000
14 25149.1667 12365.8333
15 26133.3333 14500.0000
16 26150.0000 10550.0000
17 26283.3333 12766.6667
18 26433.3333 13433.3333
19 26550.0000 13850.0000
20 26733.3333 11683.3333
21 27026.1111 13051.9444
22 27096.1111 13415.8333
23 27153.6111 13203.3333
24 27166.6667 9833.3333
25 27233.3333 10450.0000
26 27233.3333 11783.3333
27 27266.6667 10383.3333
28 27433.3333 12400.0000
29 27462.5000 12992.2222
EOF
Листинг 2.1. wi29: 29 городов в Западной Сахаре.
Оптимальное решение wi29

Оптимальное решение wi29
Тип данных: эвклидовы координаты городов
1 11511.3889 42106.3889
2 11503.0556 42855.2778
3 11438.3333 42057.2222
4 11438.3333 42057.2222
5 11438.3333 42057.2222
6 11785.2778 42884.4444
7 11785.2778 42884.4444
8 11785.2778 42884.4444
9 11785.2778 42884.4444
10 12363.3333 43189.1667
11 11846.9444 42660.5556
12 11503.0556 42855.2778
13 11963.0556 43290.5556
14 11963.0556 43290.5556
15 12300.0000 42433.3333
16 11973.0556 43026.1111
17 11973.0556 43026.1111
18 11461.1111 43252.7778
19 11461.1111 43252.7778
20 11461.1111 43252.7778
21 11461.1111 43252.7778
22 11600.0000 43150.0000
23 12386.6667 43334.7222
24 12386.6667 43334.7222
25 11595.0000 43148.0556
26 11595.0000 43148.0556
27 11569.4444 43136.6667
28 11310.2778 42929.4444
29 11310.2778 42929.4444
30 11310.2778 42929.4444
31 11963.0556 43290.5556
32 11416.6667 42983.3333
33 11416.6667 42983.3333
34 11595.0000 43148.0556
35 12149.4444 42477.5000
36 11595.0000 43148.0556
37 11595.0000 43148.0556
38 11108.6111 42373.8889
39 11108.6111 42373.8889
40 11108.6111 42373.8889
41 11108.6111 42373.8889
42 11183.3333 42933.3333
43 12372.7778 42711.3889
44 11583.3333 43150.0000
45 11583.3333 43150.0000
46 11583.3333 43150.0000
47 11583.3333 43150.0000
48 11583.3333 43150.0000
49 11822.7778 42673.6111
50 11822.7778 42673.6111
51 12058.3333 42195.5556
52 11003.6111 42102.5000
53 11003.6111 42102.5000
54 11003.6111 42102.5000
55 11522.2222 42841.9444
56 12386.6667 43334.7222
57 12386.6667 43334.7222
58 12386.6667 43334.7222
59 11569.4444 43136.6667
60 11569.4444 43136.6667
61 11569.4444 43136.6667
62 11155.8333 42712.5000
63 11155.8333 42712.5000
64 11155.8333 42712.5000
65 11155.8333 42712.5000
66 11133.3333 42885.8333
67 11133.3333 42885.8333
68 11133.3333 42885.8333
69 11133.3333 42885.8333
70 11133.3333 42885.8333
71 11003.6111 42102.5000
72 11770.2778 42651.9444
73 11133.3333 42885.8333
74 11690.5556 42686.6667
75 11690.5556 42686.6667
76 11751.1111 42814.4444
77 12645.0000 42973.3333
78 12421.6667 42895.5556
79 12421.6667 42895.5556
80 11485.5556 43187.2222
81 11423.8889 43000.2778
82 11423.8889 43000.2778
83 11715.8333 41836.1111
84 11297.5000 42853.3333
85 11297.5000 42853.3333
86 11583.3333 43150.0000
87 11569.4444 43136.6667
88 12286.9444 43355.5556
89 12355.8333 43156.3889
EOF
Листинг 2.2. dj89: 89 городов в Джибути
Оптимальный тур dj89

Оптимальный тур dj89
Тип данных: координаты городов
1 6734 1453
2 2233 10
3 5530 1424
4 401 841
5 3082 1644
6 7608 4458
7 7573 3716
8 7265 1268
9 6898 1885
10 1112 2049
11 5468 2606
12 5989 2873
13 4706 2674
14 4612 2035
15 6347 2683
16 6107 669
17 7611 5184
18 7462 3590
19 7732 4723
20 5900 3561
21 4483 3369
22 6101 1110
23 5199 2182
24 1633 2809
25 4307 2322
26 675 1006
27 7555 4819
28 7541 3981
29 3177 756
30 7352 4506
31 7545 2801
32 3245 3305
33 6426 3173
34 4608 1198
35 23 2216
36 7248 3779
37 7762 4595
38 7392 2244
39 3484 2829
40 6271 2135
41 4985 140
42 1916 1569
43 7280 4899
44 7509 3239
45 10 2676
46 6807 2993
47 5185 3258
48 3023 1942


EOF
Листинг 2.3. att48: 48 городских центров США (Padberg/Rinaldi) 
1
8
38
31
44
18
7
28
6
37
19
27
17
43
30
36
46
33
20
47
21
32
39
48
5
42
24
10
45
35
4
26
2
29
34
41
16
22
3
23
14
25
13
11
12
15
40
9
-1
EOF
Листинг 2.4. Оптимальное решение att48 
Тип данных – транспонированная диагональная матрица
97 205 139 86 60 220 65 111 115 227 95 82 225 168 103 266 205 149 120 58 257 152 52 180 136 82 34 145
129 103 71 105 258 154 112 65 204 150 87 176 137 142 204 148 148 49 41 211 226 116 197 89 153 124 74
219 125 175 386 269 134 184 313 201 215 267 248 271 274 236 272 160 151 300 350 239 322 78 276 220 60
167 182 180 162 208 39 102 227 60 86 34 96 129 69 58 60 120 119 192 114 110 192 136 173 173
 51 296 150 42 131 268 88 131 245 201 175 275 218 202 119 50 281 238 131 244 51 166 95 69
279 114 56 150 278 46 133 266 214 162 302 242 203 146 67 300 205 111 238 98 139 52 120
178 328 206 147 308 172 203 165 121 251 216 122 231 249 209 111 169 72 338 144 237 331
169 151 227 133 104 242 182 84 290 230 146 165 121 270 91 48 158 200 39 64 210
172 309 68 169 286 242 208 315 259 240 160 90 322 260 160 281 57 192 107 90
140 195 51 117 72 104 153 93 88 25 85 152 200 104 139 154 134 149 135
320 146 64 68 143 106 88 81 159 219 63 216 187 88 293 191 258 272
174 311 258 196 347 288 243 192 113 345 222 144 274 124 165 71 153
144 86 57 189 128 71 71 82 176 150 56 114 168 83 115 160
 61 165 51 32 105 127 201 36 254 196 136 260 212 258 234
106 110 56 49 91 153 91 197 136 94 225 151 201 205
215 159 64 126 128 190 98 53 78 218 48 127 214
 61 155 157 235 47 305 243 186 282 261 300 252
105 100 176 66 253 183 146 231 203 239 204
113 152 127 150 106 52 235 112 179 221
 79 163 220 119 164 135 152 153 114
236 201 90 195 90 127 84 91
273 226 148 296 238 291 269
112 130 286 74 155 291
130 178 38 75 180
281 120 205 270
213 145 36
 94 217
162
Листинг 2.5. bayg29: 29 городов в Баварии, географические расстояния (Groetschel, Juenger, Reinelt) 
Тип данных: полная матрица
 0 107 241 190 124 80 316 76 152 157 283 133 113 297 228 129 348 276 188 150 65 341 184 67 221 169 108 45 167
 107 0 148 137 88 127 336 183 134 95 254 180 101 234 175 176 265 199 182 67 42 278 271 146 251 105 191 139 79
 241 148 0 374 171 259 509 317 217 232 491 312 280 391 412 349 422 356 355 204 182 435 417 292 424 116 337 273 77
 190 137 374 0 202 234 222 192 248 42 117 287 79 107 38 121 152 86 68 70 137 151 239 135 137 242 165 228 205
 124 88 171 202 0 61 392 202 46 160 319 112 163 322 240 232 314 287 238 155 65 366 300 175 307 57 220 121 97
 80 127 259 234 61 0 386 141 72 167 351 55 157 331 272 226 362 296 232 164 85 375 249 147 301 118 188 60 185
 316 336 509 222 392 386 0 233 438 254 202 439 235 254 210 187 313 266 154 282 321 298 168 249 95 437 190 314 435
 76 183 317 192 202 141 233 0 213 188 272 193 131 302 233 98 344 289 177 216 141 346 108 57 190 245 43 81 243
 152 134 217 248 46 72 438 213 0 206 365 89 209 368 286 278 360 333 284 201 111 412 321 221 353 72 266 132 111
 157 95 232 42 160 167 254 188 206 0 159 220 57 149 80 132 193 127 100 28 95 193 241 131 169 200 161 189 163
 283 254 491 117 319 351 202 272 365 159 0 404 176 106 79 161 165 141 95 187 254 103 279 215 117 359 216 308 322
 133 180 312 287 112 55 439 193 89 220 404 0 210 384 325 279 415 349 285 217 138 428 310 200 354 169 241 112 238
 113 101 280 79 163 157 235 131 209 57 176 210 0 186 117 75 231 165 81 85 92 230 184 74 150 208 104 158 206
 297 234 391 107 322 331 254 302 368 149 106 384 186 0 69 191 59 35 125 167 255 44 309 245 169 327 246 335 288
 228 175 412 38 240 272 210 233 286 80 79 325 117 69 0 122 122 56 56 108 175 113 240 176 125 280 177 266 243
 129 176 349 121 232 226 187 98 278 132 161 279 75 191 122 0 244 178 66 160 161 235 118 62 92 277 55 155 275
 348 265 422 152 314 362 313 344 360 193 165 415 231 59 122 244 0 66 178 198 286 77 362 287 228 358 299 380 319
 276 199 356 86 287 296 266 289 333 127 141 349 165 35 56 178 66 0 112 132 220 79 296 232 181 292 233 314 253
 188 182 355 68 238 232 154 177 284 100 95 285 81 125 56 66 178 112 0 128 167 169 179 120 69 283 121 213 281
 150 67 204 70 155 164 282 216 201 28 187 217 85 167 108 160 198 132 128 0 88 211 269 159 197 172 189 182 135
 65 42 182 137 65 85 321 141 111 95 254 138 92 255 175 161 286 220 167 88 0 299 229 104 236 110 149 97 108
 341 278 435 151 366 375 298 346 412 193 103 428 230 44 113 235 77 79 169 211 299 0 353 289 213 371 290 379 332
 184 271 417 239 300 249 168 108 321 241 279 310 184 309 240 118 362 296 179 269 229 353 0 121 162 345 80 189 342
 67 146 292 135 175 147 249 57 221 131 215 200 74 245 176 62 287 232 120 159 104 289 121 0 154 220 41 93 218
 221 251 424 137 307 301 95 190 353 169 117 354 150 169 125 92 228 181 69 197 236 213 162 154 0 352 147 247 350
 169 105 116 242 57 118 437 245 72 200 359 169 208 327 280 277 358 292 283 172 110 371 345 220 352 0 265 178 39
 108 191 337 165 220 188 190 43 266 161 216 241 104 246 177 55 299 233 121 189 149 290 80 41 147 265 0 124 263
 45 139 273 228 121 60 314 81 132 189 308 112 158 335 266 155 380 314 213 182 97 379 189 93 247 178 124 0 199
 167 79 77 205 97 185 435 243 111 163 322 238 206 288 243 275 319 253 281 135 108 332 342 218 350 39 263 199 0
Листинг 2.6. bays29: 29 городов в Баварии, расстояния по дорогам (Groetschel, Juenger, Reinelt) 
 1 1150.0 1760.0
 2  630.0 1660.0
 3  40.0 2090.0
 4  750.0 1100.0
 5  750.0 2030.0
 6 1030.0 2070.0
 7 1650.0 650.0
 8 1490.0 1630.0
 9  790.0 2260.0
 10  710.0 1310.0
 11  840.0 550.0
 12 1170.0 2300.0
 13  970.0 1340.0
 14  510.0 700.0
 15  750.0 900.0
 16 1280.0 1200.0
 17  230.0 590.0
 18  460.0 860.0
 19 1040.0 950.0
 20  590.0 1390.0
 21  830.0 1770.0
 22  490.0 500.0
 23 1840.0 1240.0
 24 1260.0 1500.0
 25 1280.0 790.0
 26  490.0 2130.0
 27 1460.0 1420.0
 28 1260.0 1910.0
 29  360.0 1980.0
EOF
Листинг 2.7. bays29: координаты городов 
1
28
6
12
9
26
3
29
5
21
2
20
10
4
15
18
14
17
22
11
19
25
7
23
8
27
16
13
24
-1
EOF
Листинг 2.8. bayg29:лучшие решения 
bays29: лучший тур

1
28
6
12
9
26
3
29
5
21
2
20
10
4
15
18
14
17
22
11
19
25
7
23
8
27
16
13
24
-1
EOF
Листинг 2.9. bays29: лучший тур 
Тип данных: эвклидовы координаты
1 565.0 575.0
2 25.0 185.0
3 345.0 750.0
4 945.0 685.0
5 845.0 655.0
6 880.0 660.0
7 25.0 230.0
8 525.0 1000.0
9 580.0 1175.0
10 650.0 1130.0
11 1605.0 620.0 
12 1220.0 580.0
13 1465.0 200.0
14 1530.0 5.0
15 845.0 680.0
16 725.0 370.0
17 145.0 665.0
18 415.0 635.0
19 510.0 875.0 
20 560.0 365.0
21 300.0 465.0
22 520.0 585.0
23 480.0 415.0
24 835.0 625.0
25 975.0 580.0
26 1215.0 245.0
27 1320.0 315.0
28 1250.0 400.0
29 660.0 180.0
30 410.0 250.0
31 420.0 555.0
32 575.0 665.0
33 1150.0 1160.0
34 700.0 580.0
35 685.0 595.0
36 685.0 610.0
37 770.0 610.0
38 795.0 645.0
39 720.0 635.0
40 760.0 650.0
41 475.0 960.0
42 95.0 260.0
43 875.0 920.0
44 700.0 500.0
45 555.0 815.0
46 830.0 485.0
47 1170.0 65.0
48 830.0 610.0
49 605.0 625.0
50 595.0 360.0
51 1340.0 725.0
52 1740.0 245.0
EOF
Листинг 2.10. berlin52: 52 здания in Berlin (Groetschel) 
	
1
49
32
45
19
41
8
9
10
43
33
51
11
52
14
13
47
26
27
28
12
25
4
6
15
5
24
48
38
37
40
39
36
35
34
44
46
16
29
50
20
23
30
2
7
42
21
17
3
18
31
22
-1
EOF
Листинг 2.11. berlin52: лучший тур 
Тип данных: эвклидовы координаты городов
1 37 52
2 49 49
3 52 64
4 20 26
5 40 30
6 21 47
7 17 63
8 31 62
9 52 33
10 51 21
11 42 41
12 31 32
13 5 25
14 12 42
15 36 16
16 52 41
17 27 23
18 17 33
19 13 13
20 57 58
21 62 42
22 42 57
23 16 57
24 8 52
25 7 38
26 27 68
27 30 48
28 43 67
29 58 48
30 58 27
31 37 69
32 38 46
33 46 10
34 61 33
35 62 63
36 63 69
37 32 22
38 45 35
39 59 15
40 5 6
41 10 17
42 21 10
43 5 64
44 30 15
45 39 10
46 32 39
47 25 32
48 25 55
49 48 28
50 56 37
51 30 40
EOF
Листинг 2.12. eil51: 51 город (Christofides/Eilon) 
1
22
8
26
31
28
3
36
35
20
2
29
21
16
50
34
30
9
49
10
39
33
45
15
44
42
40
19
41
13
25
14
24
43
7
23
48
6
27
51
46
12
47
18
4
17
37
5
38
11
32
-1
EOF
Листинг 2.13. eil51: лучший тур 
Тип данных: эвклидовы координаты городов
1 22 22
2 36 26
3 21 45
4 45 35
5 55 20
6 33 34
7 50 50
8 55 45
9 26 59
10 40 66
11 55 65
12 35 51
13 62 35
14 62 57
15 62 24
16 21 36
17 33 44
18 9 56
19 62 48
20 66 14
21 44 13
22 26 13
23 11 28
24 7 43
25 17 64
26 41 46
27 55 34
28 35 16
29 52 26
30 43 26
31 31 76
32 22 53
33 26 29
34 50 40
35 55 50
36 54 10
37 60 15
38 47 66
39 30 60
40 30 50
41 12 17
42 15 14
43 16 19
44 21 48
45 50 30
46 51 42
47 50 15
48 48 21
49 12 38
50 15 56
51 29 39
52 54 38
53 55 57
54 67 41
55 10 70
56 6 25
57 65 27
58 40 60
59 70 64
60 64 4
61 36 6
62 30 20
63 20 30
64 15 5
65 50 70
66 57 72
67 45 42
68 38 33
69 50 4
70 66 8
71 59 5
72 35 60
73 27 24
74 40 20
75 40 37
76 40 40
EOF
Листинг 2.14. eil76: 76 городов (Christofides/Eilon) 
1
33
63
16
3
44
32
9
39
72
58
10
31
55
25
50
18
24
49
23
56
41
43
42
64
22
61
21
47
36
69
71
60
70
20
37
5
15
57
13
54
19
14
59
66
65
38
11
53
7
35
8
46
34
52
27
45
29
48
30
4
75
76
67
26
12
40
17
51
6
68
2
74
28
62
73
-1
EOF
Листинг 2.15. eil76: лучший тур

Краткие итоги:

  • рассмотрено применение ГА при решении задач комбинаторной оптимизации;
  • представлен простой ГА для решения задачи укладки рюкзака;
  • описано решение задачи о покрытии с помощью ГА;
  • рассмотрено решение задачи коммивояжера с помощью ГА;
  • описаны различные формы кодирования потенциальных решений задачи коммивояжера и соответствующие проблемно-ориентированные операторы кроссинговера;
  • представлены эволюционные методы решения задачи сокращения диагностической информации.
Дальше >>
< Лекция 1 || Лекция 2: 1234567 || Лекция 3 >

Вопросы и ответы

вопросов: 0