Эволюционные стратегии
Эволюционные стратегии (ЭС), также как и предыдущие парадигмы, основаны на эволюции популяции потенциальных решений, но, в отличие от них, здесь используется генетические операторы на уровне фенотипа, а не генотипа, как это делается в ГА. Разница в том, что ГА работают в пространстве генотипа – кодов решений, в то время как ЭС производят поиск в пространстве фенотипа – векторном пространстве вещественных чисел. В ЭС учитываются свойства хромосомы "в целом", в отличие от ГА, где при поиске решений исследуются отдельные гены. В природе один ген может одновременно влиять на несколько свойств организма. С другой стороны одно свойство особи может определяться несколькими генами. Естественная эволюция основана на исследовании совокупности генов, а не отдельного (изолированного) гена.
В эволюционных стратегиях целью является движение особей популяции по направлению к лучшей области ландшафта фитнесс-функции. ЭС изначально разработаны для решения многомерных оптимизационных задач, где пространство поиска – многомерное пространство вещественных чисел [1]. Иногда при решении задачи накладываются некоторые ограничения, например, вида 
.
Ранние эволюционные стратегии (ЭС) основывались на популяции, состоящей из одной особи, и в них использовался только один генетический оператор – мутация. Здесь для представления особи (потенциального решения) была использована идея, не представленная в классическом генетическом алгоритме, которая заключается в следующем.
Здесь особь представляется парой действительных векторов
 |
( 9.1) |
где 
- точка в пространстве решений и 
- вектор стандартных отклонений (вариабельность) от решения. В общем случае особь популяции определяется вектором потенциального решения и вектором "стратегических параметров" эволюции. Обычно это вектор стандартных отклонений (дисперсия), хотя допускаются (и иногда используются) и другие статистики.
Единственным генетическим оператором в классической ЭС [1] является оператор мутации, который выполняется путем сложения координат вектора-родителя со случайными числами, подчиняющимися закону нормального распределения, следующим образом:
 |
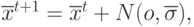( 9.2) |
где 
- вектор независимых случайных чисел, генерируемых согласно распределению Гаусса (например, табличным способом) с нулевым средним значением и стандартным отклонением 
. Как видно из приведенной формулы величина мутации управляется нетрадиционным способом. Иногда эволюционный процесс используется для изменения и самих стратегических параметров , в этом случае величина мутации эволюционирует вместе с искомым потенциальным решением. Это соответствует адаптивному ГА с изменяемым шагом мутации.
Интуитивно ясно, что увеличение отклонения подобно увеличению шага поиска на поверхности ландшафта. Высокая вариабельность способствует расширению пространства поиска и эффективна при нахождении потенциальных зон (суб)оптимальных решений и соответствует высоким значениям коэффициента мутации. В тоже время малые значения вариабельности позволяют сфокусироваться на поиске решения в перспективной области. В данном случае стратегические параметры стохастически определяют величину шага поиска: большая вариабельность ведет к большим шагам. Отметим, что поскольку отклонения генерируются стохастически (по нормальному закону), то большая вариабельность может давать маленький шаг и наоборот. Известно, что 68,26% случайных чисел при нормальном распределении попадают в интервал, определяемый стандартным отклонением ; 95% чисел попадают в интервал 1,96 и т.д.