Эволюционные стратегии
9.5. Сравнение эволюционной стратегии и генетических алгоритмов
Эволюционные стратегии применяются, в основном, в численной оптимизации, так как они были (по крайней мере, первоначально) посвящены функциональным задачам оптимизации в вещественной области. ЭС позволяет эффективно решать многие задачи стандартной и сложной нелинейной оптимизации с ограничениями (и без них) [11,12].
Они являются примерами эволюционных программ, которые используют соответствующие структуры данных (вещественные векторы, расширенные параметрами стратегии управления) и "генетические" операторы, ориентированные на решение определенных задач.
Основная разница между этими методами состоит в кодировании особей. Эволюционная стратегия была создана и развивалась для решения задач численной оптимизации. Поэтому решение (особь) представляется в виде вектора вещественных чисел. Хотя в настоящее время известны новые работы, в которых ЭС применяется для решения задач дискретной оптимизации.
С другой стороны, генетические алгоритмы были разработаны в качестве общего метода решения оптимизационных задач. В простом классическом ГА особь представляется в виде двоичного вектора.
Поэтому, может быть, не совсем корректно сравнивать эти два направления, так как они были разработаны для разных целей. Но их объединяет принцип отбора лучших решений (отбор по Дарвину сильнейших особей). Однако имеются существенные различия между этими подходами.
Первое различие между ЭС и ГА - это форма представления решений. ЭС использует вектор вещественных чисел, ГА – двоичный.
Второе различие между ГА и ЭС скрыто в процедуре выбора. В ЭС  -особей родителей порождают промежуточную популяцию, которая состоит из
-особей родителей порождают промежуточную популяцию, которая состоит из  -потомков, путем оператора мутации и репродукции. На промежуточной популяции выполняется процедура отбора, которая сокращает эту популяцию обычно до исходной. В простейшем случае оставляются
-потомков, путем оператора мутации и репродукции. На промежуточной популяции выполняется процедура отбора, которая сокращает эту популяцию обычно до исходной. В простейшем случае оставляются  лучших особей – решение (причем все они разные).
лучших особей – решение (причем все они разные).
В ГА оператор репродукции ОР (аналог процедуры выбора) генерирует промежуточную популяцию, причем число представителей каждой особи зависит от значений целевой функции для этих особей. Т.е. сильнейшие представители промежуточной популяции имеют нескольких представителей, и наоборот, наиболее слабые особи промежуточной популяции могут быть не представлены. Далее случайным образом производится выбор пар для выполнения ОК и ОМ.
Третье различие заключается в относительном порядке выполнения процедур отбора и рекомбинации. В ЭС процедура отбора выполняется после выполнения оператора репродукции. В ГА наоборот, ОР работает перед ОК и ОМ.
Следующее различие в том, что в классическом ГА параметры операторов рекомбинации обычно остаются постоянными (вероятность ОМ, ОК), а в ЭС параметры  изменяются.
изменяются.
ЭС и ГА по разному учитывают ограничения: в ЭС есть множество неравенств 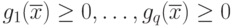 , которое рассматривается как часть оптимизационной задачи. В ГА ограничения обычно учитываются в виде штрафных функций, т.е. в неявном виде.
, которое рассматривается как часть оптимизационной задачи. В ГА ограничения обычно учитываются в виде штрафных функций, т.е. в неявном виде.
Из выше сказанного следует, что ЭС и ГА, хотя и имеют много общего, но и имеют существенные отличия. Но в настоящее время есть явная тенденция сближения этих двух направлений. С одной стороны современные ГА часто используются для представления решения векторами вещественных чисел, с другой стороны ЭС в качестве ОР использует не только ОМ, но и операторы типа ОК.
