Эволюционные вычисления
[+]
Московский государственный университет путей сообщения
Опубликован: 10.10.2014 | Доступ: свободный | Студентов: 869 / 193 | Длительность: 22:10:00
Тема: Алгоритмы и дискретные структуры
Специальности: Программист, Архитектор программного обеспечения
Лекция 9:

Эволюционные стратегии
A
|
версия для печати
< Лекция 8 || Лекция 9: 1234567 || Лекция 10 >

9.1. Двукратная эволюционная (1+1)- стратегия

Здесь потомок принимается в качестве нового члена популяции (он заменяет своего родителя), если значение фитнесс функции (ЦФ) на нем лучше, чем у его родителя и выполняются все ограничения. Иначе, (если значение фитнесс-функции на нем хуже, чем у родителей), потомок уничтожается и популяция остается неизменной.

Рассмотрим выполнение оператора мутации на конкретном примере следующей функции [2]

f(x_1,x_2)=21,5+x_1\cdot\sin(4\pi x_1)+x_2\cdot\sin(20\pi x_2)\\-3.0\le x_1\le 12.1\quad\overline x=(x_1,x_2)\\4.1\le x_2\le 5.8\quad\overline\sigma=(\sigma_1,\sigma_2) ( 9.3)

в предположении поиска максимума.

Для определенности предположим, что в t-поколении текущая особь имеет вид:

(\overline x^t,\sigma)=((5.3;4.9),(1.0;1.0)). ( 9.4)

Тогда потомок определяется следующим образом:

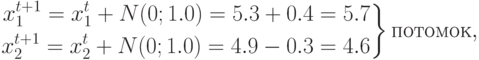\left\begin{aligned}x_1^{t+1}=x_1^t+N(0;1.0)=5.3+0.4=5.7\\x_2^{t+1}=x_2^t+N(0;1.0)=4.9-0.3=4.6\\\end{aligned}\right\}\mbox{потомок}, ( 9.5)

где числа 0.4 и 0.3 получены случайным образом в соответствии с распределением Гаусса.

Поскольку f(x^t)=f(5.3;4.9)=18.383705<24.849532=f(5.7;4.6)=f(x^{t+1}) (значение ЦФ потомка лучше, чем у родителя), то полученный потомок заменяет родителя.

В целом алгоритм процесса эволюции двукратной (1+1)- эволюционной стратегии можно сформулировать следующим образом.

  1. Выбрать множество P параметров X, необходимых для представления решения данной проблемы, и определить диапазон допустимых изменений каждого параметра:\{x_{1\min},x_{1\max}\},\{x_{2min},x_{2\max}\},\dots,\{x_{P\min},x_{P\max}\},

    установить номер поколения (итерации) 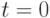t=0; задать стандартное отклонение 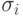\sigma_i для каждого параметра, функцию f, для которой необходимо найти оптимум, и максимальное число поколений k.

  2. Для каждого параметра случайным образом выбрать начальное значение из допустимого диапазона: множество этих значений составляет начальную популяцию (из одной особи) X^t=(x_1,x_2,\dots,x_P).
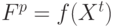  3. Вычислить значение оптимизируемой функции f для родительской особи F^p=f(X^t).
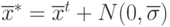
  4. Создать новую особь-потомка в соответствии с (9.2) \overline x^*=\overline x^t+N(0,\overline\sigma)
  5. Вычислить значение f для особи-потомка F^0=f(X^*).
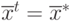  6. Сравнить значения функций f для родителя и потомка; если значение потомка F^0 лучше, чем у родительской особи, то заменить родителя на потомка \overline x^t=\overline x^*, иначе оставить в популяции родителя.
  7. Увеличить номер поколения t=t+1;
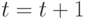  8. Если не достигнуто максимальное число поколений 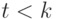t<k, то переход на шаг 4, иначе выдать найденное решение X^t.

Несмотря на то, что фактически здесь популяция состоит из одной особи, рассмотренная стратегия называется двукратной ЭС. Причина в том, что здесь фактически происходит конкуренция потомка и родителя. Обычно вектор стандартных отклонений \sigma остается неизменным в течении всего процесса эволюции. Если все его компоненты одинаковы и оптимизационная задача регулярна, то можно доказать следующую теорему сходимости [1,2].

Теорема. Для \sigma>0 и регулярной оптимизационной задачи с f_{opt}>-\infty (минимизация), либо f_{opt}>+\infty(максимизация), имеет место равенство

P\{\lim_{t\to\infty}f(\overline x^t)=f_{opt}\}1 ( 9.6)

Эта теорема утверждает, что оптимальное решение регулярной оптимизационной задачи находится с вероятностью, равной единице при t\to\infty, но при этом совершенно ничего не говорится о том, как и каким образом двигаться к этому оптимальному решению. Поэтому, чтобы оптимизировать скорость сходимости этого процесса, И. Решенберг [1] (основоположник ЭС) предложил правило успеха "1/5".

Смысл его заключается в следующем - правило применяется после каждых k поколений процесса (где k – параметр этого метода):

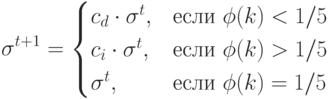\sigma^{t+1}=\begin{cases}c_d\cdot\sigma^t,&\text{если $\phi(k)<1/5$}\\c_i\cdot\sigma^t,&\text{если $\phi(k)>1/5$}\\\sigma^t,&\text{если $\phi(k)=1/5$}\end{cases} ( 9.7)

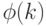где \phi(k)- отношение числа успешных мутаций к общему числу произведенных мутаций k(число успехов, деленное на k), которое называется коэффициентом успеха для оператора мутации в течении k последних поколений; величина c_i>1,c_d<1 – регулирует увеличение/уменьшение отклонения мутации.

Обычно на практике оптимальные значения полагают равными следующим величинам: c_d=0.82; c_i=1/0.82=1.22.. Смысл этого правила в следующем:

  • если коэффициент успеха 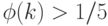\phi(k)>1/5, то отклонение 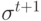\sigma^{t+1} увеличивается (мы идем более крупными шагами);
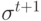  • если коэффициент успеха \phi(k)<1/5, то отклонение \sigma^{t+1} уменьшается (шаг поиска уменьшается).

Идеи И.Решенберга получили дальнейшее развитие в концепции "эволюция окна" [3] при которой результат применения оператора мутации принимается только в том случае, если он лежит в пределах некоторой окрестности (окна) родительской особи в пространстве решений. Динамическое изменение шага мутации в сочетании с эволюцией величины окна ведет к метаэволюции [3].

Иногда рекомендуется устанавливать коэффициент мутации обратно пропорционально числу переменных в потенциальном решении (особи) и прямо пропорционально расстоянию от точки оптимального решения. Конечно, в реальных приложениях точное расположение оптимума неизвестно. Однако иногда может быть известна априорная информация об оптимуме (например, порядок величины). Даже ограниченная информация может быть полезна в процессе поиска в ЭС.

Дальше >>
< Лекция 8 || Лекция 9: 1234567 || Лекция 10 >

Вопросы и ответы

вопросов: 0