Эволюционные вычисления
[+]
Московский государственный университет путей сообщения
Опубликован: 10.10.2014 | Доступ: свободный | Студентов: 869 / 193 | Длительность: 22:10:00
Тема: Алгоритмы и дискретные структуры
Специальности: Программист, Архитектор программного обеспечения
Лекция 9:

Эволюционные стратегии
A
|
версия для печати
< Лекция 8 || Лекция 9: 1234567 || Лекция 10 >

9.4. Генетические операторы ЭС

В ЭС, как и в большинстве методов эволюционных вычислений, могут использоваться три генетических оператора: отбора, кроссинговера и мутации.

9.4.1 Операторы отбора

В ЭС отбор особей используется для: 1) выбора родителей, которые принимают участие в рекомбинации; 2) для формирования популяции следующего поколения. Для отбора \rho родителей оператора кроссинговера может быть использован любой из методов, рассмотренных в разделе 3.3. Часто родительские особи выбираются случайно.

В каждом поколении \lambda потомков генерируются из \mu родителей и подвергаются мутации. После кроссинговера и мутации отбираются особи в следующее поколение. При этом применяются две основные стратегии:

  1. (\mu+\lambda)-ЭС, где из \mu родителей генерируется \lambda потомков (1\le\mu\le\lambda<\infty) и отбор \mu лучших особей в следующее поколение (обычно с применением элитизма) производится среди объединенного множества ( (\mu+\lambda) особей) родителей и потомков;
  2. (\mu,\lambda)-ЭС, где \mu -особей родителей порождает \lambda-потомков, причем \mu>\lambda и процесс выбора лучших производится только на множестве потомков.

Учитывая приведенные нотации, иногда используется (\mu^+,\lambda)-ЭС обозначение. В некоторых случаях нотация (\mu+\lambda)-ЭС расширяется до (\mu,k,\lambda), где k обозначает максимальную продолжительность жизни особи. Если число поколений превышает этот предел, то особь не может отбираться в следующее поколение. Заметим, что (\mu,\lambda)-ЭС эквивалентна (\mu,1,\lambda)-ЭС. Выбор лучшей стратегии зависит от решаемой задачи.

9.4.2. Операторы кроссинговера

В классической (1+1)-ЭС используется только оператор мутации. В последующих модификациях, начиная с (\mu+1)-ЭС допускается применение операторов кроссинговера. При этом оператор может применяться как на уровне генотипа (векторов вещественных чисел), так и параметров и реализуется способом, отличным от других парадигм ЭВ. Реализация отличается по возможному числу родителей, участвующих в рекомбинации и по способу комбинации генетического материала и значений параметров. В общем случае нотация (\mu/\rho,^+,\lambda) используется для указания того, что \rho родителей используется при реализации оператора кроссинговера. На основе значений этих родительских особей потомки генерируются путем применения:

  1. локального кроссинговера \rho=2, где один потомок производится из двух случайно взятых родителей;
  2. глобального кроссинговера 2<\rho\le\mu, где более чем два родителя используются для генерации потомка. Чем больше значение \rho, тем больше возможное разнообразие у получаемых потомков.

Поэтому глобальный кроссинговер улучшает эксплутационные свойства ЭС.

В обоих случаях рекомбинация может выполняться следующим образом:

  • Дискретная рекомбинация, значения родительских особей используются для получения значений генов потомков, как описано в разделе 3.3. Для каждой компоненты потомка берется компонента одного из родителей (как описано в разделе 3.3). Нотация 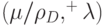(\mu/\rho_D,^+\lambda) используется для обозначения дискретной рекомбинации.
  • Промежуточная рекомбинация, где значение особи-потомка получается путем взвешенной арифметической суммы родительских особей (как описано в разделе 3.3). Нотация (\mu/\rho_I,^+\lambda) используется для обозначения промежуточной рекомбинации.

На основе приведенных выше типов рекомбинации в ЭС разработаны и применяются следующие основные пять видов рекомбинации:

  • Нет рекомбинации: Если X_i(t)- родительская особь, то она переходит в следующее поколение в качестве потомка \tilde X_i=X_i(t).
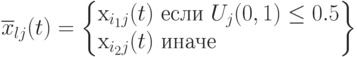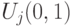  • Локальная дискретная рекомбинация, где \overline x_{lj}(t)=\left\{\begin{array}{}x_{i_1j}(t)\mbox{ если $U_j(0,1)\le 0.5$}\\x_{i_2j}(t)\mbox{ иначе}\end{array}\right\} и U_j(0,1)- случайное число в диапазоне (0,1).Здесь потомок \overline x_{l}(t)=(\overline x_{l}(t),\overline\sigma_l(t),\overline\omega_l(t)) наследует свойства обоих родителей x_{i_1}(t)=(x_{i_1}(t),\sigma_{i_1}(t),\omega_{i_2}(t)) и x_{i_2}(t)=(x_{i_2}(t),\sigma_{i_2}(t),\omega_{i_2}(t))
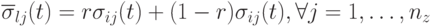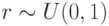  • Локальная промежуточная рекомбинация, где \overline x_{lj}(t)=rx_{ij}(t)+(1-r)x_{ij}(t),\forall j=1,\dots,n_z и \overline\sigma_{lj}(t)=r\sigma_{ij}(t)+(1-r)\sigma_{ij}(t),\forall j=1,\dots,n_z с r\sim U(0,1).Если используются углы вращения, то \omega_{lj}=[rx_{i_1k}(t)+(1-r)\sigma_{i_2k}(t)]\mod 2\pi,\forall k=1,\dots,n_x(n_x-1).
  • Глобальная дискретная рекомбинация, где \overline x_{lj}(t)=\left\{\begin{array}{}x_{i_1j}(t)\mbox{ если $U_j(0,1)\le 0.5$}\\x_{r_jj}(t)\mbox{ иначе}\end{array}\right\} с r_j\sim\Omega_l, где \Omega_l множество индексов \rho родителей, отобранных для выполнения кроссинговера.
  • Глобальная промежуточная рекомбинация походит на локальную промежуточную рекомбинацию за исключением того, что индекс 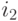i_2 заменяется на r_j\sim\Omega_l. Есть альтернативный вариант этого оператора, когда потомок вычисляется на основе средних значений родителей
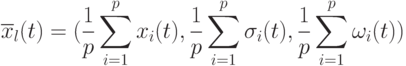
    \overline x_l(t)=(\frac{1}{p}\sum_{i=1}^p x_i(t),\frac{1}{p}\sum_{i=1}^p\sigma_i(t),\frac{1}{p}\sum_{i=1}^p\omega_i(t)) ( 9.18)
    .

В [9] предложена арифметическая рекомбинация между лучшей и средней по всем родителям особью:

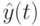\overline x_l(t)=r\hat{y}(t)+(1-r)\frac{1}{p}\sum_{i\in\Omega_i}^p x_i(t)
, где \hat{y}(t)- лучшая особь текущей популяции. Этот подход применим и к построению значений параметров ЭС. Данная стратегия ведет к тому, что потомок располагается в окрестности лучшей особи.

9.4.3. Операторы мутации

После выполнения оператора кроссинговера полученные потомки с вероятностью p_m=1 подвергаются мутации. Оператор мутации выполняется в два шага для каждого потомка следующим образом:

  • На первом шаге производится самоадаптация параметров одним из методов, изложенных ранее.
  • На втором шаге выполняется собственно мутация x'_l(t)=\overline x_l(t)+\Delta x_l(t).

При этом \lambda мутируемых потомков x'_{l}(t)=(x'_{l}(t),\overline\sigma_l(t),\overline\omega_l(t)) принимают участие в процессе отбора (наравне со своими родителями) в зависимости от того, какая стратегия - (\mu+\lambda)-ЭС или (\mu,\lambda)-ЭС используется. В данном разделе рассматривается только мутация значений генотипа, поскольку мутация и самоадаптация параметров изложены ранее.

Если в качестве параметров используются только отклонения, генотип \tilde x_l(t) каждого потомка мутирует в соответствии с правилами:

  • Если n_{\sigma}=1,\Delta x_{lj}(t)=\sigma_l(t)N_j(0,1),\forall j=1,\dots,n_x
  • Если n_{\sigma}=n_x,\Delta x_{lj}(t)=\sigma_{lj}(t)N_j(0,1),\forall j=1,\dots,n_x
  • Если 1<n_{\sigma}<n_x,\Delta x_{lj}(t)=\sigma_{lj}(t)N_j(0,1),\forall j=1,\dots,n_{\sigma}\ and\ \Delta x_{lj}(t)=\sigma_{ln_{\sigma}}(t)N_j(0,1),\forall j=n_{\sigma}+1,\dots,n_x

Если, кроме этого, используются и углы вращения, то в предположении n_{\sigma}=,n_x приращение вычисляется согласно выражению

\Delta x_l(t)=T(\overline\omega_l(t))S(\overline\sigma_l(t))N(0,1),

где T(\tilde\omega(t))- ортогональная матрица вращения

T(\overline\omega_l(t))=\prod_{a=1}^{n_z-1}\prod_{b=a+1}^{n_z}R_{ab}(\overline\omega_l(t)),

которая является произведением n_x(n_x-1)/2 матриц вращения. Каждая матрица вращения R_{ab}(\overline\omega_l(t))- единичная матрица, где элементы определяются следующим образом: r=\cos(\tilde\omega_{lk}),r_{ab}=-r_{ab}=-sin(\tilde\omega_{lk}) для k=1,\dots,n_x(n_x-1)/2 и k=1\Leftrightarrow(a=1,b=2),\ k=2\Leftrightarrow(a=1,b=3),\dots S(\tilde\sigma_l(t))-diagn(\tilde\sigma_{l1}(t),\tilde\sigma_{l}(t),\dots,\tilde\sigma_{ln_x}(t)) - диагональная матрица, представляющая отклонения.

В работе [10] предложена направленная мутация, где предпочтение отдается некоторому направлению в пространстве поиска. Как показано нарис.9.2, она основана на асимметричном вероятностном распределении мутации. Здесь размер шага по оси x_2 больше, чем по оси x_1 и отдается предпочтение положительным направлениям.

Направленная мутация в ЭС.

Рис. 9.2. Направленная мутация в ЭС.

При этом каждый компонент генотипа мутирует независимо и поэтому достаточно определить одномерную асимметричную функцию плотности вероятностей, например в виде

f_D(x)=\left\{\begin{array}{cl}\frac{2}{\sqrt{\pi\sigma}(1+\sqrt{1+c}}(e^{-\frac{z^2}{\sigma}})&\mbox{если $x<0$}\\\frac{2}{\sqrt{\pi\sigma}(1+\sqrt{1+c}}(e^{-\frac{z^2}{\sigma(1+c)}})&\mbox{если $x\ge 0$}\\\end{array}\right\} ( 9.20)

где c>0 положительно определенная величина.

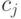Метод направленной мутации использует только параметры отклонений, но ассоциирует с каждым отклонением \sigma_j значение c_j, определяющее направление. Для обеих величин \sigma и c возможна само-адаптация, что дает 2n_x параметров. С вычислительной точки зрения это более эффективно, чем использование вектора вращения размерности n_x(n_x-1)/2 и дает больше информации о предпочтительном направлении и размере шага.

Если 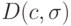D(c,\sigma) означает асимметричное распределение, то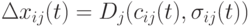 \Delta x_{ij}(t)=D_j(c_{ij}(t),\sigma_{ij}(t))

В работе [7] предложен инвариантный в системе координат оператор мутации с самоадаптацией, где генотип мутирует, используя значения отклонений и корреляций следующим образом:

x'_l(t)=\frac{1}{p}\sum_{i\in\Omega_l(t)} x_i(t)+\overline\sigma_l N(0,C_l(t)). ( 9.21)
Дальше >>
< Лекция 8 || Лекция 9: 1234567 || Лекция 10 >

Вопросы и ответы

вопросов: 0