Эволюционные вычисления
[+]
Московский государственный университет путей сообщения
Опубликован: 10.10.2014 | Доступ: свободный | Студентов: 869 / 193 | Длительность: 22:10:00
Тема: Алгоритмы и дискретные структуры
Специальности: Программист, Архитектор программного обеспечения
Лекция 9:

Эволюционные стратегии
A
|
версия для печати
< Лекция 8 || Лекция 9: 1234567 || Лекция 10 >

9.2. Многократная эволюционная стратегия

По сравнению с двукратной многократная эволюция отличается не только размером популяции 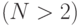(N > 2), но и имеет некоторые дополнительные отличия:

  • все особи в поколении имеют одинаковую вероятность выбора для мутации;
  • имеется возможность введения оператора рекомбинации (например, однородного ОК в ГА, рассмотренного в разделе 4), где два случайно выбранных родителя производят потомка по следующей схеме:
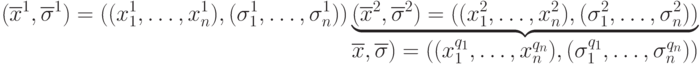
    (\overline x^1,\overline\sigma^1)=((x_1^1,\dots,x_n^1),(\sigma_1^1,\dots,\sigma_n^1))\\\underbrace{(\overline x^2,\overline\sigma^2)=((x_1^2,\dots,x_n^2),(\sigma_1^2,\dots,\sigma_n^2))}_{\mbox{$\overline x,\overline\sigma)=((x_1^{q_1},\dots,x_n^{q_n}),(\sigma_1^{q_1},\dots,\sigma_n^{q_n}))$}} ( 9.8)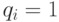
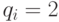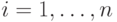    где q_i=1 или q_i=2, i=1,\dots,n (т.е. каждая компонента потомка копируется из первого или второго родителя).

Имеется еще одно сходство между двукратными и многократными эволюционными стратегиями. При обоих видах ЭС производится только один потомок. В двукратных стратегиях потомок соревнуется со своим родителем. В многократной стратегии самая слабая особь уничтожается.

В современной литературе используются следующие обозначения:

  • (1+1)-ЭС - двукратная стратегия (1 родитель производит 1 потомка);
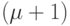  • (\mu+1)-ЭС - многократная стратегия (\mu родителей производят 1 потомка);
  • (\mu+\lambda)-ЭС, где \mu-родителей производят \lambda-потомков и отбор \mu лучших представителей производится среди объединенного множества ((\mu+\lambda) особей) родителей и потомков;
  • (\mu,\lambda)-ЭС, где \mu особей родителей порождает \lambda потомков, причем \lambda>\mu и процесс выбора лучших производится только на множестве потомков.

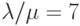Следует подчеркнуть, что в обоих последних видах ЭС обычно число потомков существенно больше числа родителей \lambda>\mu(иногда полагают \lambda/\mu=7).

Укрупненный алгоритм решения задачи с помощью ЭС можно представить следующим образом.


Здесь на этапе инициализации генерируются особи начальной популяции со значениями в пределах ограничений и задаются начальные значения параметров. Для оценки качества особи используется абсолютное значение фитнесс-функции. Далее выполняются генетические операторы отбора, кроссинговера и мутации, наиболее распространенные варианты которых представлены ниже. В качестве критерия останова может быть использован любой из рассмотренных ранее.

Дальше >>
< Лекция 8 || Лекция 9: 1234567 || Лекция 10 >

Вопросы и ответы

вопросов: 0