Модификации генетических алгоритмов
3.2.7. Метод Больцмана
В этом случае при отборе особей используется подход, который используется в известном методе оптимизации "моделирование отжига", где при управлении процессом поиска применяется "искусственная температура". Для этого вводится действительная переменная  , которая, начиная с некоторого достаточно большого значения, постепенно уменьшается (по определенному закону) и изменяет вероятность отбора особей. Вероятность отбора особи, имеющей значение фитнесс-функции
, которая, начиная с некоторого достаточно большого значения, постепенно уменьшается (по определенному закону) и изменяет вероятность отбора особей. Вероятность отбора особи, имеющей значение фитнесс-функции 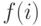 , определяется следующим образом
, определяется следующим образом
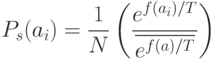 |
( 3.3) |
где 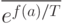 представляет среднее значение
представляет среднее значение 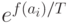 по текущей популяции. Отметим, что с уменьшением температуры разность значений
по текущей популяции. Отметим, что с уменьшением температуры разность значений 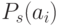 между худшими и лучшими особями увеличивается. Это позволяет на заключительном этапе сузить поиск в наиболее перспективной области пространства поиска, сохраняя при этом достаточную степень разнообразия в популяции. Показано, что для некоторых задач этот метод отбора дает лучшие результаты, чем стандартный пропорциональный отбор типа "рулетка"[3].
между худшими и лучшими особями увеличивается. Это позволяет на заключительном этапе сузить поиск в наиболее перспективной области пространства поиска, сохраняя при этом достаточную степень разнообразия в популяции. Показано, что для некоторых задач этот метод отбора дает лучшие результаты, чем стандартный пропорциональный отбор типа "рулетка"[3].
3.2.8. Методы выбора пар для скрещивания
До сих пор мы, в основном, рассматривали методы отбора родителей в промежуточную популяцию. Далее из этой популяции необходимо выбрать пары особей для выполнения операции скрещивания. Основными методами выбора пар особей являются следующие.
Случайный выбор (панмиксия) родительской пары, при котором оба родителя случайным образом выбираются из всей промежуточной популяции. Следует отметить, что при этом любая особь может входить в несколько пар. Этот метод является универсальным для решения различных задач, но достаточно критичен к численности популяции, поскольку его эффективность снижается с ростом мощности популяции  .
.
Селективный выбор. Здесь родителями могут стать только те особи, значение целевой функции которых не меньше среднего значения по популяции при равной вероятности этих кандидатов составить брачную пару. Такой подход обеспечивает более быструю сходимость алгоритма, но неприемлем для мультимодальных задач (имеющих несколько экстремумов), для которых этот метод, как правило, быстро сходится к одному из решений. Это может привести к преждевременной сходимости к локальному экстремуму.
Часто используется также два следующих подхода: инбридинг и аутбридинг. В них формирование пары происходит на основе близкого или дальнего родства соответственно. Под родством обычно понимается расстояние между особями популяции в пространстве параметров. В связи с этим различают генотипный и фенотипный инбридинг и аутбридинг.
Инбридинг – здесь первый член пары выбирается случайно, а вторым является максимально близкая к нему особь.
Аутбридинг формирует пары из максимально далеких особей.
Комбинация этих походов используется при решении многоэкстремальных задач.
3.2.9. Неявные методы отбора, основанные на масштабировании фитнесс-функции
Кроме рассмотренных выше явных методов отбора часто применяются также и неявные методы, которые, как правило, сводятся к масштабированию фитнесс-функции [1,4]. Масштабирование фитнесс-функции производится обычно в следующих случаях: 1) для предотвращения преждевременной сходимости ГА; 2) на последнем этапе выполнения ГА, когда в популяции сохраняется значительная неоднородность, однако среднее значение фитнесс-функции ненамного отличается от максимального значения. Масштабирование позволяет избежать ситуаций, в которых средние и лучшие особи дают практически одинаковое количество потомков, что считается нежелательным явлением. Преждевременная сходимость соответствует ситуации, когда в популяции доминируют лучшие, но еще не оптимальные особи. Это особенно характерно для ГА, использующих при отборе родителей метод рулетки. При этом часто возникают ситуации, когда через несколько поколений популяция состоит в основном из копий лучшей особи. Поскольку в качестве исходной популяции часто используется небольшая случайная выборка из пространства возможных решений, то маловероятно, что именно эта лучшая особь соответствует оптимальному решению. Масштабирование фитнесс-функции часто позволяет избежать доминирования неоптимальной особи, и, тем самым, предохраняет ГА от преждевременной сходимости.
Масштабирование выполняется с помощью трех основных преобразований фитнесс-функций: 1) линейное, 2) сигма-отсечение и 3) степенное.
Линейное масштабирование сводится к линейному преобразованию фитнесс-функции следующего вида

где  и
и  - константы, которые обычно подбираются так, чтобы среднее значение фитнесс-функции после масштабирования было равно ее среднему значению до масштабирования, а максимальное значение фитнесс-функции после преобразования было кратным ее среднему значению. Здесь
- константы, которые обычно подбираются так, чтобы среднее значение фитнесс-функции после масштабирования было равно ее среднему значению до масштабирования, а максимальное значение фитнесс-функции после преобразования было кратным ее среднему значению. Здесь  и
и 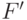 соответствуют фитнесс-функции до и после преобразования. При этом коэффициент кратности обычно выбирается в пределах от 1,2 до 2 и необходимо следить, чтобы новая фитнесс-функция
соответствуют фитнесс-функции до и после преобразования. При этом коэффициент кратности обычно выбирается в пределах от 1,2 до 2 и необходимо следить, чтобы новая фитнесс-функция 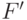 не принимала отрицательных значений.
не принимала отрицательных значений.
Сигма отсечение основано на следующем преобразовании фитнесс-функции
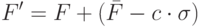 |
( 3.4) |
где  означает среднее значение фитнесс-функции по популяции,
означает среднее значение фитнесс-функции по популяции,  – малое натуральное число (обычно от 1 до 5), а
– малое натуральное число (обычно от 1 до 5), а  - стандартное отклонение по популяции. Если при этом значения
- стандартное отклонение по популяции. Если при этом значения 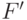 получаются отрицательными, то они полагаются равными нулю.
получаются отрицательными, то они полагаются равными нулю.
При степенном масштабировании используется следующее преобразование

где  – число, обычно близкое к 3. В общем случае
– число, обычно близкое к 3. В общем случае  подбирается эвристическим путем с учетом специфики задачи.
подбирается эвристическим путем с учетом специфики задачи.
