Модификации генетических алгоритмов
3.2.3. Равномерное ранжирование (случайный выбор)
Здесь вероятность выбора особи определяется выражением:
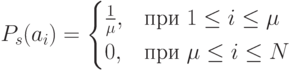 |
( 3.2) |
где 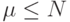 параметр метода.
параметр метода.
3.2.4. Локальный отбор
Производится среди особей, которые находятся в некоторой ограниченной среде, где определено отношение соседства. Ранее, фактически, в качестве соседей каждой особи рассматривалась вся популяция. При этом в качестве соседей подразумевается множество партнеров для выполнения операции скрещивания.
Соседство можно определить по-разному. Далее рассмотрим типичные отношения соседства, используемые при локальном отборе.
- Линейное соседство:
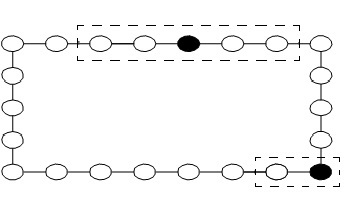
На рис.3.4 представлен пример линейного соседства. На практике рассматривают полную окрестность (на рис.3.4 вверху показана полная окрестность выделенного элемента с расстоянием
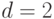 ) и "полуокрестность" (в правом нижнем углу рисунка показана "полуокрестность" с расстоянием
) и "полуокрестность" (в правом нижнем углу рисунка показана "полуокрестность" с расстоянием  ).
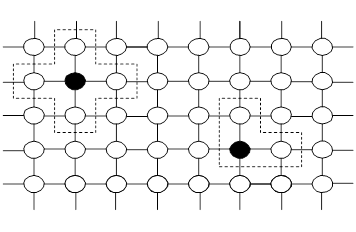
). - Двумерное – четырехсвязное соседство. На рис.3.5 представлен пример соседства с 4-связностью (в левом верхнем углу показан полный "крест" выделенного элемента с расстоянием
 , справа "полукрест" также с расстоянием
, справа "полукрест" также с расстоянием  ).
).
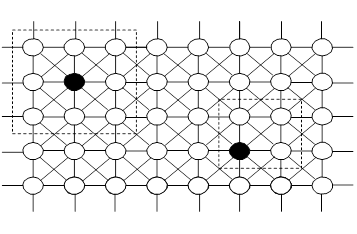
- Двумерное – восьмисвязное соседство.
На рис.3.6 представлен пример соседства с 8-связностью (в левом верхнем углу показан полная "звезда" выделенного элемента с расстоянием
 , а справа "полузвезда"). Для определения отношения можно также использовать гексагональную решетку с 6-связностью и даже трехмерные структуры.При отборе родителей на первом шаге производится отбор особей случайным образом, или одним из ранее рассмотренных способов. Далее для каждой отобранной особи определяется множество локальных соседей и среди них выбирается партнер для выполнения операции скрещивания.При наличии отношения соседства, между особями возникает эффект "изоляции расстоянием". Очевидно, что чем меньше соседство, тем больше "изоляция расстоянием". Это ограничивает распространение новых решений в популяции.
, а справа "полузвезда"). Для определения отношения можно также использовать гексагональную решетку с 6-связностью и даже трехмерные структуры.При отборе родителей на первом шаге производится отбор особей случайным образом, или одним из ранее рассмотренных способов. Далее для каждой отобранной особи определяется множество локальных соседей и среди них выбирается партнер для выполнения операции скрещивания.При наличии отношения соседства, между особями возникает эффект "изоляции расстоянием". Очевидно, что чем меньше соседство, тем больше "изоляция расстоянием". Это ограничивает распространение новых решений в популяции.
Однако, из-за перекрытия соседних областей, распространение новых вариантов решений все же возможно. Мощность множества соседей определяет скорость распространения информации между особями популяции, способствуя либо быстрому распространению новых решений, либо сохранению имеющегося генофонда в популяции. Часто при решении задачи требуется высокая изменчивость, которая поможет избежать преждевременной сходимости в районе локального оптимума. Обычно локальный отбор в малом окружении дает лучшие результаты, чем в большем окружении.
В малых и средних популяциях  для локального отбора рекомендуется двумерная структура типа "полузвезда" с расстоянием
для локального отбора рекомендуется двумерная структура типа "полузвезда" с расстоянием  .При большом размере популяции
.При большом размере популяции  лучше использовать большие расстояния
лучше использовать большие расстояния  и двумерные структуры с соседством типа "звезда".
и двумерные структуры с соседством типа "звезда".
3.2.5. Отбор на основе усечения
Предыдущие методы отбора в какой то степени заимствованы у (или имеют аналогию с) эволюции естественных популяций. Этот метод не имеет аналогов в естественной эволюции и обычно используется для больших популяций  . При этом сначала отбираемые особи упорядочиваются согласно их значениям целевой функции. Затем в качестве родителей выбираются только лучшие особи. Далее, с равной вероятностью, среди них случайным образом выбирают пары, которые производят потомков.
. При этом сначала отбираемые особи упорядочиваются согласно их значениям целевой функции. Затем в качестве родителей выбираются только лучшие особи. Далее, с равной вероятностью, среди них случайным образом выбирают пары, которые производят потомков.
При этом методе используется параметр – порог отсечения  (иногда используется термин интенсивность отбора), показывающий долю (часть популяции), которая отбирается в качестве родителей. Обычно
(иногда используется термин интенсивность отбора), показывающий долю (часть популяции), которая отбирается в качестве родителей. Обычно 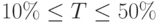 .
.
3.2.6. Турнирный отбор
В этом случае все особи популяции разбиваются на подгруппы размера  с последующим выбором в каждой из них особи с лучшим значением фитнесс-функции. Параметром этой процедуры является размер тура
с последующим выбором в каждой из них особи с лучшим значением фитнесс-функции. Параметром этой процедуры является размер тура  , который принимает значения из диапазона
, который принимает значения из диапазона 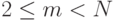 . Используются два способа выбора - детерминированный и случайный. При детерминированном способе выбор выполняется с вероятностью, равной 1, в то время как при случайном методе выбор осуществляется с вероятностью меньше 1. Чаще всего популяция разбивается на подгруппы по 2-3 особи в каждой (
. Используются два способа выбора - детерминированный и случайный. При детерминированном способе выбор выполняется с вероятностью, равной 1, в то время как при случайном методе выбор осуществляется с вероятностью меньше 1. Чаще всего популяция разбивается на подгруппы по 2-3 особи в каждой ( ).Рис.3.7 иллюстрирует метод турнирной селекции для подгрупп, состоящих из двух особей.Турнирный метод может быть использован как при максимизации, так и при минимизации функции. Кроме этого, он легко распространяется на задачи многокритериальной оптимизации. Экспериментальные исследования показывают, что часто данный метод эффективней метода рулетки.
).Рис.3.7 иллюстрирует метод турнирной селекции для подгрупп, состоящих из двух особей.Турнирный метод может быть использован как при максимизации, так и при минимизации функции. Кроме этого, он легко распространяется на задачи многокритериальной оптимизации. Экспериментальные исследования показывают, что часто данный метод эффективней метода рулетки.