Модификации генетических алгоритмов

3.11 Адаптивные генетические алгоритмы

В последние годы проведено достаточно много исследований в этом направлении, когда в основном рассматриваются два вида адаптации:

1. Адаптация к проблеме;
2. Адаптация к процессу эволюции.

Разница между ними в том, что первая модифицирует некоторые компоненты ГА, такие как вид представления особи, кроссинговер, мутация и отбор. Естесственно, для удачного выбора или модификации компонентов необходимо понимать суть решаемой задачи. Во втором виде адаптации предлагается способ настройки значений параметров и конфигурации ГА в процессе решения задачи. Следуя [15, 16] последний вид адаптации можно разбить на следующие классы:

• адаптация параметров установки;
• адаптация генетических операторов;
• адаптация отбора;
• адаптация представления решения;
• адаптация фитнесс-функции.

Из этих видов в последние десять лет исследовались различные способы адаптации параметров, таких как вероятности кроссинговера и мутации, мощность популяции, которые играют решающую роль в балансе расширения и эксплуатации пространства поиска решений. Ключевым вопросом является выбор значений параметров для эффективного решения данной проблемы. Обычно в простом ГА используются фиксированные значения параметров, которые находятся методом проб и ошибок. Поскольку сам ГА является динамическим и адаптивным процессом, то фиксированные значения параметров противоречат самому духу эволюции. Поэтому возникла естественная идея попробовать изменять значения параметров в процессе поиска решения. Это можно сделать различными способами:

• применять некоторые правила;
• использовать обратную связь в виде информации о текущем состоянии поиска;
• внедрить некоторый механизм самоадаптации.

В работах [15,17] представлен обзор используемых на текущий момент методов адаптации в ГА, в котором выделены три основные категории.

1. Детерминированная адаптация, где значение параметра изменяется по некоторому детерминированному правилу. Например, вероятность мутации уменьшается в соответствии со следующей формулой: , где – номер текущего поколения (итерации) и – максимально допустимое число поколений. Согласно этому правилу вероятность мутации уменьшается от 0.5 до 0.3 при росте номера поколения эволюции.
2. Адаптивная адаптация, которая имеет место при наличии некоторой формы обратной связи с процессом эволюции и используется для определения направления изменения параметра. Одним из первых примеров является "правило успеха 1/5" Решенберга в эволюционных стратегиях (см. раздел 9.1) для определения коррекции шага мутации. Правило гласит, что если доля успешных мутаций (дающих улучшение решения) больше 1/5, то шаг мутации можно увеличить, в противном случае этот шаг следует уменьшить. Известны примеры адаптивных фитнесс-функций [18], адаптивного механизма поиска соотношения между значениями вероятностей кроссинговера и мутации [19] и т.п.
3. Самоадаптация, где значения параметров также эволюционируют в процессе поиска решений. При этом значения параметров кодируются и включаются в хромосомы особей, но не учитываются при вычислении значений фитнесс-функции.

3.11.1. Адаптация мощности популяции

Отметим, что изменение мощности популяции между двумя соседними поколениями прежде всего влияет на функционирование оператора отбора. Пусть и 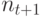обозначают мощность популяции текущего и последующего поколения соответственно. Отбор особей можно рассматривать как повторяющийся процесс 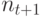операторов отбора с вероятностью 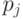для -ой особи. Для большинства методов отбора, таких, как например, пропорциональный или турнирный отбор с замещением, вероятность выбора 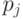остается неизменной при выполнении 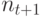операторов. Тогда ожидаемое количество копий -ой особи можно выразить как , где 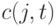– число копий -ой особи в поколении . Ожидаемое количество копий -ой особи прямо пропорционально мощности популяции следующего поколения. Таким образом, долю в популяции особей, связанных с -ой особью после отбора можно выразить следующим выражением:

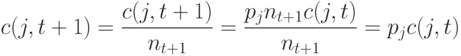
которое не зависит от размера следующей популяции на том основании, что изменение мощности популяции несущественно влияет на значение вероятности 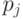. Отметим, что ГА, где мощность популяции уменьшается с ростом поколения, имеет большую начальную и меньшую конечную популяцию. Это повышает эффективность ГА, поскольку большая начальная популяция покрывает большее подпространство поиска, а в конце процесса, когда найдена "зона интереса", для сходимости к оптимуму достаточно и небольшого количества особей в популяции

Основываясь на этих предположениях, был предложен так называемый пилообразный ГА [20], где изменение мощности популяции комбинируется с реинициализацией, которая выполняется для улучшения характеристик ГА. При этом среднее значение мощности популяции 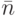по периоду соответствует постоянной популяции ГА с той же вычислительной сложностью. Кроме этого, закон изменения мощности популяции характеризуется амплитудой и периодом . В этой нотации размер популяции изменяется следующим образом:

На рис.3.22 представлен пример пилообразного изменения мощности популяции.

Рис. 3.22. Пилообразное изменение количества особей в популяции