Модификации генетических алгоритмов

3.11.2. Адаптация вероятностей кроссинговера и мутации

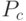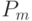В адаптивных генетических алгоритмах изменяются параметры ГА, прежде всего, вероятности кроссинговера и мутации и . Для оптимизации, особенно мультимодальных функций, наиболее существенными являются две характеристики ГА:

• способность сходиться к оптимуму (локальному или глобальному) после нахождения области, содержащей этот оптимум;
• способность находить новые области в пространстве решений в поисках глобального оптимума.

Баланс между этими характеристиками ГА определяется значениями вероятност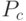и и 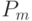и типом используемых генетических операторов (прежде всего кроссинговера). Увеличение значени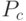й и 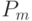ведет к расширению пространства поиска.

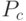Обычно используют следующие значения вероятностей - и . Далее мы рассмотрим другой подход [7], который использует различные значения и 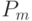в зависимости от значения ЦФ текущих особей. Для мультимодальных функций существует серьезная проблема преждевременной сходимости к локальным экстремумам.

Чтобы изменять 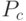и 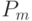адаптивно, с целью предотвращения преждевременной сходимости к локальному экстремуму, надо научиться идентифицировать ситуации, когда ГА сходится к оптимуму. Рассмотрим этот подход на примере поиска максимума для мультимодальной функции (которая имеет несколько экстремумов), которая показана на рис. 3.23

Рис. 3.23. Мультимодальная функция

Один из возможных способов обнаружения сходимости – наблюдение разности среднего и максимального значения целевой функции по популяции 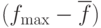. Обычно эта разность меньше для популяции, которая сходится к оптимуму, чем для популяции, "разбросанной" по пространству поиска решений. Будем использовать разность 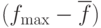в качестве основного признака сходимости к оптимуму, причем не обязательно глобальному.

Поскольку вероятност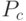и и 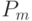должны увеличиваться при преждевременной сходимости к локальному оптимуму (чтобы "выпрыгнуть из ловушки" локального экстремума), то значение 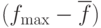должны изменяться обратно пропорционально разности :

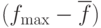( 3.21)

Здесь 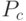и 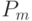не зависят от значений ЦФ для конкретной особи, а определяются для всей популяции, но для разных популяций различных поколений они уже будут разными.

Отметим, что как для хороших решений с высокими значениями целевой функции, так и для плохих, используются одни и те же величины 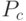и 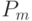. Это не рационально, так как когда популяция сходится к глобальному или локальному оптимуму, то 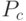и 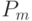увеличиваются, что ведет к разрушению близких к оптимуму решений. В результате популяция может не сойтись к глобальному оптимуму. Таким образом, мы избежали ловушки локального экстремума ценой снижения характеристик ГА по поиску глобальных экстремумов.

Чтобы решить эту проблему, нужно сохранить хорошие решения текущей популяции. Это можно сделать, полагая низкие значения вероятност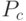и и 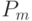для особей с высоким значением ЦФ и высокие значения 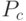и 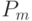для плохих особей с низкими значениями ЦФ. Тогда лучшие решения будут способствовать сходимости, а худшие – предотвращать ГА от "ловушек" локальных экстремумов. Таким образом, значение 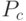и 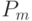должны зависеть не только от разности 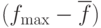, но еще и от значений ЦФ конкретных особей. Чем ближе значение функции к максимальному, тем меньше должно быть значение 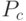и :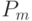

( 3.22)

где 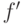– лучшее значение целевой функции у двух родителей.

Положим для решений, имеющих максимальное значение ЦФ и

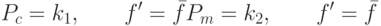( 3.23)

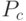Отметим, что для плохих решений значения вероятностей и 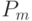в соответствии с формулой (3.23) могут быть больше 1, что некорректно. Поэтому для плохих решений примем:

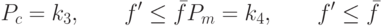
В итоге получим:

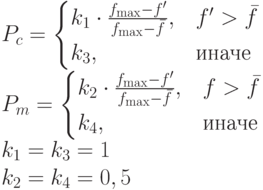( 3.24)

Лучшие решения при этом сохраняются и переходят в следующее поколение. Этот факт может привести к чрезмерному росту популяции, что чревато преждевременной сходимостью. Поэтому иногда дополнительно вводится одна (default) мутация (с вероятностью 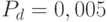) для всех особей популяции.

Существуют и более строгие адаптивные ГА, где вероятност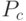и и 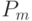вычисляются аналитически, но они, как правило, сильно привязаны к конкретным задачам. Достаточно эффективным средством адаптации является использование "нечетких контроллеров" в виде, например, системы продукций в нечеткой логике.