|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Потоки в сетях
Программа 22.7 является клиентской программой, которая считывает задачу о двудольном сопоставлении из стандартного ввода и решает ее при помощи сведения, описанного в этом доказательстве. Каким будет время выполнения этой программы для очень больших сетей? Разумеется, время выполнения зависит от используемого алгоритма вычисления максимального потока и его реализации. Кроме того, следует учесть, что получаемые при этом сети имеют специальную структуру (двудольные транспортные сети с единичной пропускной способностью ребер). Поэтому время выполнения различных известных нам алгоритмов вычисления максимальных потоков не приближается к границам для худшего случая; более того, можно существенно снизить эти границы. Например, нетрудно улучшить оценку для первой рассмотренной нами границы - для обобщенного алгоритма с использованием расширяющих путей.
Следствие. Время вычисления сопоставления максимальной мощности для двудольного графа равно O(VE).
Доказательство. Непосредственно следует из леммы 22.6. 
Работу алгоритмов расширения путей на двудольной сети с единичной пропускной способностью ребер описать нетрудно. Каждый расширяющий путь наполняет одно ребро, ведущее из истока, и одно ребро, ведущее в сток. Эта ребра никогда не используются как обратные, поэтому может быть не более V расширяющих путей. Для каждого алгоритма, который находит расширяющие пути за время, пропорциональное E, действительна верхняя граница, пропорциональная VE.
Программа 22.7. Поиск двудольного сопоставления сведением к задаче вычисления максимального потока
Этот клиент считывает из стандартного ввода задачу о двудольном сопоставлении с V + V вершинами и E ребрами, а затем строит транспортную сеть, соответствующую этой задаче, находит максимальный поток в сети и использует полученное решение для вывода максимального двудольного сопоставления.
#include "GRAPHbasic.cc"
#include "MAXFLOW.cc"
int main(int argc, char *argv[])
{ int s, t, N = atoi(argv[1]);
GRAPH<EDGE> G(2*N+2);
for (int i = 0; i < N; i++)
G.insert(new EDGE(2*N, i, 1));
while (cin >> s >> t)
G.insert(new EDGE(s, t, 1));
for (int i = N; i < 2*N; i++)
G.insert(new EDGE(i, 2*N+1, 1));
MAXFLOW<GRAPH<EDGE>, EDGE>(G, 2*N, 2*N+1);
for (int i = 0; i < N; i++)
{ GRAPH<EDGE>::adjIterator A(G, i);
for (EDGE* e = A.beg(); !A.end(); e = A.nxt())
if (e->flow() == 1 && e->from(i))
cout << e->v() << "-" << e->w() << endl;
}
}
В таблице 22.3 показаны значения производительности для методов решения задач двудольного сопоставления с использованием различных алгоритмов вычисления расширяющих путей. Из этой таблицы видно, что фактические значения времени решения этой задачи ближе к значению VE для худшего случая, чем к оптимальному (линейному) времени. Разумный выбор и соответствующая настройка реализации, вычисляющей максимальный поток, позволяет увеличить быстродействие этого метода в 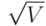 раз (см. упражнения 22.91 и 22.92).
раз (см. упражнения 22.91 и 22.92).
Здесь представлены показатели производительности (количество расширенных вершин и количество затронутых узлов в списках смежности) для различных алгоритмов вычисления максимального потока методом расширения путей при вычислении максимального двудольного сопоставления для графов с 2000 парами вершин и 500 ребрами (вверху), а также 4000 ребрами (внизу). Для этой задачи наиболее эффективным оказался поиск в глубину.
| Вершины | Ребра | |
|---|---|---|
| 500 ребер, мощность сопоставления 347 | ||
| Кратчайший путь | 1071 | 945599 |
| Максимальная пропускная способность | 1067 | 868407 |
| Поиск в глубину | 1073 | 477601 |
| Случайный поиск | 1073 | 644070 |
| 4000 ребер, мощность сопоставления 971 | ||
| Кратчайший путь | 3483 | 8280585 |
| Максимальная пропускная способность | 6857 | 6573560 |
| Поиск в глубину | 34109 | 1266146 |
| Случайный поиск | 3569 | 4310656 |
Эта задача - характерный случай, с которым мы чаще сталкиваемся при изучении новых задач и более общих моделей решения задач, и который демонстрирует эффективность сведения как практического средства решения задач. Если мы сможем найти сведение к известной общей задаче - например, к задаче о максимальном потоке - мы обычно рассматриваем это как существенное продвижение на пути к практическому решению. Ведь оно, по меньшей мере, указывает не только на разрешимость задачи, но и на существование многочисленных эффективных алгоритмов решения рассматриваемой задачи. Во многих случаях для решения такой задачи проще использовать существующий класс вычисления максимального потока и перейти к следующей задаче. Если производительность критична, можно опробовать различные алгоритмы вычисления максимальных потоков и их реализации или разработать на основе их поведения более совершенный алгоритм специального назначения. Общая модель решения задачи предоставляет верхнюю границу, которую можно либо принять, либо попытаться улучшить, и множество реализаций, которые продемонстрировали свою эффективность при решении многих других задач.
Далее мы обсудим задачи, имеющие отношение к связности графов. Но прежде чем рассматривать использование алгоритмов вычисления максимального потока для решения задач связности, мы исследуем применение теоремы о максимальном потоке и минимальном сечении и завершим то, что начали в "Поиск на графе" - доказательства базовых теорем, относящихся к путям и сечениям в неориентированных графах. Эти доказательства еще раз подчеркивают фундаментальное значение теоремы о максимальном потоке и минимальном сечении.
Лемма 22.20. (Теорема Менгера). Минимальное количество ребер, удаление которых разъединяет две вершины в орграфе, равно максимальному количеству не пересекающихся по ребрам путей между этими двумя вершинами.
Доказательство. Для заданного графа определим транспортную сеть с теми же вершинами и ребрами, при этом пропускные способности всех ребер равны 1. Согласно лемме 22.2 любую st-сеть можно представить в виде множества не пересекающихся по ребрам путей из истока в сток, а количество таких путей равно величине потока. Пропускная способность любого st-сечения равна мощности этого сечения. Из всех этих фактов и теоремы о максимальном потоке и минимальном сечении вытекает нужный результат. 
Соответствующие результаты для неориентированных графов и для вершинной связности в орграфах и неориентированных графах получаются с помощью сведений, подобных рассмотренным в тексте, и оставлены на самостоятельную проработку (упражнения 22.94-22.96).
А теперь обратимся к алгоритмическим следствиям из непосредственной взаимосвязи между потоками и связностью, которая устанавливается теоремой о максимальном потоке и минимальном сечении. Пожалуй, одним из важнейших алгоритмических следствий является лемма 22.5 (задача о минимальном сечении сводится к задаче о максимальном потоке), однако обратное утверждение не доказано (см. упражнение 22.47). Вроде бы информация о минимальном сечении должна облегчить задачу вычисления максимального потока, но никому еще не удалось показать, как это сделать. Этот простой пример подчеркивает необходимость осторожности при сведении одних задач к другим.
Однако алгоритмы вычисления максимального потока все-таки можно использовать для решения различных задач о связности. Например, они помогают решить первые нетривиальные задачи, с которыми мы сталкивались в "Поиск на графе" .
Реберная связность. Каково минимальное количество ребер, которые необходимо удалить, чтобы разделить заданный граф на две части? Найти множество ребер минимальной мощности, обеспечивающее такое разделение.
Вершинная связность. Каково минимальное количество вершин, которые необходимо удалить, чтобы разделить заданный граф на две части? Найти множество вершин минимальной мощности, обеспечивающее такое разделение.
Эти задачи формулируются и для орграфов, поэтому всего требуется рассмотреть четыре задачи. Как и в случае теоремы Менгера, мы подробно рассмотрим одну из них (реберная связность в неориентированных графах), а остальные оставим читателям на самостоятельную проработку.
Лемма 22.21. Время, необходимое для определения реберной связности в неориентированном графе, равно O(E2).
Доказательство. Мы можем вычислить минимальный размер любого сечения, которое разделяет две заданные вершины - для этого нужно вычислить максимальный поток в st-сети, построенной из графа с назначением единичной пропускной способности каждому ребру. Реберная связность равна минимальному из этих значений на всех парах вершин.
Однако нет необходимости выполнять вычисления для всех пар вершин. Пусть s* - вершина графа с минимальной степенью. Ее степень не может быть больше 2E/V Рассмотрим произвольное минимальное сечение графа. По определению, количество ребер в сечении равно реберной связности графа. Вершина s* принадлежит одному из множеств вершин сечения, а в другое множество должна входить некоторая вершина t, поэтому размер любого минимального сечения, разделяющего вершины s* и t, должен быть равен реберной связности графа. Следовательно, если мы решим V- 1 задач о минимальном потоке (с s* в качестве истока и любой другой вершиной в качестве стока), то полученная величина минимального потока будет равна реберной связности сети.
Далее, любой алгоритм вычисления максимального потока с использованием расширяющих путей для вершины s* в качестве истока использует максимум 2E/V путей. Значит, если мы используем любой метод, требующий не более E шагов для определения расширяющего пути, то понадобится не более (V- 1)(2E/V)E шагов для определения реберной связности, откуда и следует искомый результат. 
Этот метод, в отличие от всех других примеров из этого раздела, не является непосредственным сведением одной задачи к другой, но он дает практический алгоритм для вычисления реберной связности. Опять-таки, тщательная настройка реализации вычисления максимального потока для этой конкретной задачи позволяет повысить производительность, и можно решить эту задачу за время, пропорциональное VE (см. раздел ссылок). Доказательство леммы 22.21 служит примером более общего понятия эффективного (выполняемого за полиномиальное время) сведения, с которым мы впервые столкнулись в "Кратчайшие пути" , и которое играет существенную роль в теории алгоритмов, о которой пойдет речь в части 8. Такое сведение не только доказывает разрешимость задачи, но и предлагает алгоритм для ее решения, а это важные первые шаги при решении новой комбинаторной задачи.
Мы завершим данный раздел анализом строгой математической формулировки задачи о максимальном потоке в терминах линейного программирования (см. "Кратчайшие пути" ). Это упражнение полезно тем, что оно помогает увидеть связи с другими задачами, которые можно сформулировать аналогично.
Формулировка этой задачи тривиальна: имеется система неравенств, в которой каждому ребру соответствует одна переменная, каждому ребру соответствуют два неравенства, и каждой вершине соответствует одно равенство. Значение переменной - это величина потока в ребре, неравенства указывают, что величина потока в ребре должна быть в пределах от нуля до пропускной способности этого ребра, а равенства указывают, что суммарный поток в ребрах, ведущих в каждую вершину, должен быть равен суммарному потоку в ребрах, исходящих из этой вершины.
Пример такого построения приведен на рис. 22.39. Аналогично любую задачу о максимальном потоке можно преобразовать в задачу линейного программирования (LP-задачу). Линейное программирование - универсальный способ решения комбинаторных задач, и многие рассматриваемые нами задачи можно сформулировать как LP-задачи. Тот факт, что задачи о максимальном потоке решаются легче, чем LP-задачи, можно объяснить тем, что в LP-формулировке задач о максимальном потоке ограничения имеют особую структуру, которая характерна не для всех LP-задач.
Эта LP-задача эквивалентна задаче о максимальном потоке для сети с рис. 22.5. Имеется по одному неравенству для каждого ребра (которое указывает, что поток в этом ребре не может превосходить его пропускной способности) и по одному равенству для каждой вершины (которое указывает, что приток должен быть равен оттоку). В этой сети используется фиктивное ребро из стока в исток, которое предназначено для перехвата сетевого потока (см. обсуждение после леммы 22.2).
Даже если LP-задача в общем виде намного сложнее, чем задачи специального вида, такие как задача о максимальном потоке, имеются мощные алгоритмы, которые могут эффективно решать LP-задачи. Время выполнения этих алгоритмов в худшем случае наверняка превосходит время выполнения в худшем случае рассмотренных нами специальных алгоритмов, однако громадный опыт, накопленный за последние несколько десятилетий, показал их эффективность при решении задач, которые часто возникают на практике.
Построение, представленное на рис. 22.39, служит доказательством того, что задача о максимальном потоке сводится к LP-задаче, если не настаивать, чтобы величины потоков были целыми числами. Мы будем подробно рассматривать LP-задачи в части VIII, и там опишем, как справиться с тем, что формулировка задачи о максимальном потоке в терминах линейного программирования не содержит требования, что результаты должны иметь целые значения.
Этот контекст дает четкую математическую основу, которая позволяет рассматривать даже более общие задачи и создавать еще более мощные алгоритмы решения этих задач. Задача о максимальном потоке легко поддается решению и сама по себе довольно универсальна, о чем говорят примеры, приведенные в данном разделе. Далее мы рассмотрим более сложную задачу (но не такую сложную, как линейное программирование), которая охватывает еще более широкий класс практических задач. Мы обсудим варианты построения решений для этих все более общих моделей в конце этой главы, заложив основу для их полного анализа в части 8.
Упражнения
22.70. Определите класс для вычисления циркуляции с максимальным потоком в заданном ребре. Разработайте реализацию, использующую функцию MAXFLOW.
22.71. Определите класс для вычисления максимального потока без ограничения на количество истоков и стоков. Разработайте реализацию, использующую функцию MAXFLOW.
22.72. Определите класс для вычисления максимального потока в неориентированной сети. Разработайте реализацию, использующую функцию MAXFLOW.
22.73. Определите класс для вычисления максимального потока в сети с ограничениями на пропускные способности вершин. Разработайте реализацию, использующую функцию MAXFLOW.
22.74. Разработайте класс для решения задач о допустимом потоке, который включает функции-члены, позволяющие клиентам устанавливать значения предложения, а затем проверять правильность выбора значений потоков для каждой вершины.
22.75. Выполните упражнение 22.18 для случая, когда в каждой точке распределения имеется ограничение на пропускную способность (т.е. существует предел количества товаров, которые могут храниться в этой точке в любой заданный момент времени).
22.76. Покажите, что задача о максимальном потоке сводится к задаче о допустимом потоке (т.е. эти задачи эквивалентны).
22.77. Найдите допустимый поток для транспортной сети, представленной на рис. 22.10, при наличии дополнительных ограничений: вершины 0, 2 и 3 являются вершинами предложения с весом 4, а вершины 1, 4 и 5 являются вершинами предложения с весами, соответственно, 1, 3 и 5.
22.78. Напишите программу, которая принимает в качестве входных данных расписание соревнований некоторой спортивной лиги и текущее положение команд и определяет, выбыла ли заданная команда из турнира. Считайте, что связи отсутствуют. Указание. Сведите данную задачу к задаче о допустимом потоке с одним истоком, величина предложения которого равна суммарному количеству игр, которые осталось сыграть в текущем сезоне; с узлами стока, соответствующими каждой паре команд, величина спроса в которых равна количеству оставшихся игр между этой парой; и с узлами распределения, соответствующими каждой команде. Ребра должны соединять узлы предложения с узлами распределения каждой команды (с пропускными способностями, равными количеству игр, которые команда должна выиграть, чтобы выиграть у X, если X выиграет все свои оставшиеся игры). И должно существовать ребро (без пропускной способности), соединяющее узел распределения каждой команды с каждым узлом спроса, имеющим отношение к этой команде.
22.79. Докажите, что задача о максимальном потоке для сетей с низкими пропускными способностями ребер сводится к стандартной задаче о максимальном потоке.
22.80. Докажите, что для сетей с низкими пропускными способностями ребер задача вычисления минимального потока (с учетом пропускных способностей) сводится к задаче о максимальном потоке (см. упражнение 22.79).
22.81. Докажите, что задача о максимальном потоке в st-сетях сводится к задаче о максимальном потоке в неориентированных сетях, либо найдите алгоритм вычисления максимального потока для неориентированных сетей, время выполнения которого в худшем случае значительно лучше, чем для алгоритмов из разделов 22.2 и 22.3.
22.82. Найдите все сопоставления с пятью ребрами для двудольного графа, представленного на рис. 22.37.
22.83. Усовершенствуйте программу 22.7, чтобы вершинам можно было присваивать символические имена, а не номера (см. программу 17.10).
22.84. Докажите, что задача двудольного сопоставления эквивалентна задаче вычисления максимального потока в сети с единичными пропускными способностями всех ребер.
22.85. Пример на рис. 22.3 можно интерпретировать как описание заявок студентов на работу и заявок работодателей на студентов, которые не обязательно взаимны. Применимо ли сведение, описанное в тексте, к ориентированной задаче двудольного сопоставления, вытекающей из этой интерпретации, где ребра двудольного графа направлены (в любом направлении) из одного множества в другое? Докажите это или приведите контрпример.
22.86. Постройте семейство задач двудольного сопоставления, где средняя длина расширяющих путей, используемых любым алгоритмом расширения путей для решения соответствующей задачи о максимальном пути, пропорциональна E.
22.87. Покажите в стиле рис. 22.28 работу алгоритма проталкивания напора с использованием очереди FIFO на сети двудольного сопоставления с рис. 22.3838.
22.88. Добавьте в таблицу 22.3 данные для различных алгоритмов проталкивания напора.
22.89. Предположим, что в задаче двудольного сопоставления два множества имеют размеры S и T, причем S << T. Приведите как можно более точную границу времени решения этой задачи в худшем случае для сведения, описанного в лемме 22.19, и реализации алгоритма Форда-Фалкерсона с использованием максимальных расширяющих путей (см. лемму 22.8).
22.90. Выполните упражнение 22.89 для реализации алгоритма проталкивания напора с использованием очереди FIFO (см. лемму 22.13).
22.91. Добавьте в таблицу 22.3 данные для реализаций, которые используют метод построения всех расширяющих путей, описанный в упражнении 22.37.
22.92. Докажите, что время выполнения метода, описанного в упражнении 22.91, равно O(JV E) для поиска в ширину.
22.93. На основе эмпирического исследования постройте график зависимости ожидаемого количества ребер в максимальном сопоставлении в случайных двудольных графах с V + V вершинами и E ребрами для разумного множества значений V и значений E, достаточных для получения гладкой кривой от ноля до V.
22.94. Докажите теорему Менгера (лемма 22.20) для неориентированных графов.
22.95. Докажите, что минимальное количество вершин, удаление которых разъединяет две вершины в орграфе, равно максимальному количеству путей между этими двумя вершинами, не пересекающихся по вершинам. Указание. Воспользуйтесь раз-щеплением вершин, как на рис. 22.32.
22.96. Распространите ваше доказательство из упражнения 22.95 на неориентированные графы.
22.97. Реализуйте класс реберной связности для АТД графа из "Виды графов и их свойства" , конструктор которого использует алгоритм, описанный в этом разделе, для обеспечения работы общедоступной функции-члена, которая возвращает значение связности графа.
22.98. Добавьте в решение упражнения 22.97 занесение в пользовательский вектор минимального множества ребер, которое разделяет граф. Какой размер этого вектора должен предусмотреть пользователь?
22.99. Разработайте алгоритм вычисления реберной связности орграфов (минимальное количество ребер, удаление которых нарушает сильную связность орграфа). На основе этого алгоритма реализуйте класс для АТД орграфа из главы 19 "Орграфы и DAG-графы" .
22.100. На основе решений упражнений 22.95 и 22.96 разработайте алгоритмы для вычисления вершинной связности орграфов и неориентированных графов. На базе этих алгоритмов реализуйте классы, соответственно, для АТД орграфа из "Орграфы и DAG-графы" , и для АТД графа из "Виды графов и их свойства" (см. упражнения 22.97 и 22.98).
22.101. Опишите, как вычислить вершинную связность орграфа путем решения VlgV задач о максимальном потоке в сети с единичными пропускными способностями. Указание. Воспользуйтесь теоремой Менгера и двоичным поиском.
22.102. Пользуясь решением упражнения 22.97, эмпирически определите реберную связность различных графов (см. упражнения 17.63-17.76).
22.103. Сформулируйте в терминах линейного программирования задачу о максимальном потоке в транспортной сети, представленную на рис. 22.10.
22.104. Сформулируйте в терминах линейного программирования задачу двудольного сопоставления, представленную на рис. 22.37.

