|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Потоки в сетях
Сведения к задаче о потоке минимальной стоимости
Поток минимальной стоимости представляет собой общую модель решения, которая может охватывать множество полезных практических задач. В данном разделе мы обоснуем это утверждение, доказав сводимость разнообразных задач к задаче о потоке минимальной стоимости.
Очевидно, что задача о потоке минимальной стоимости имеет более общий характер, чем задача о максимальном потоке, поскольку любой максимальный поток минимальной стоимости является приемлемым решением задачи о максимальном потоке. Действительно, если в построении, показанном на рис. 22.42, назначить фиктивному ребру единичную стоимость, а другим ребрам нулевую, то любой максимальный поток минимальной стоимости минимизирует поток в фиктивном ребре и, следовательно, максимизирует поток в исходной сети. Поэтому все задачи, рассмотренные в разделе 22.4, которые сводятся к задаче о максимальном потоке, сводятся и к задаче о потоке минимальной стоимости. К этому множество задач относятся, в частности, задачи о двудольном сопоставлении, о допустимом потоке и о минимальном сечении.
Однако более интересно то, что свойства полученных нами алгоритмов решения задачи о потоке минимальной стоимости позволяют разработать новые обобщенные алгоритмы решения задачи о максимальном потоке. Мы уже отмечали, что обобщенный алгоритм вычеркивания циклов для решения задачи о максимальном потоке минимальной стоимости позволяет получить обобщенный алгоритм для задачи о максимальном потоке с использованием расширяющих путей. А именно, этот подход приводит к реализации, которая находит расширяющие пути без выполнения поиска в сети (см. упражнения 22.133 и 22.134). С другой стороны, этот алгоритм может порождать расширяющие пути с нулевым потоком, что затрудняет оценку его производительности (см. раздел ссылок).
Задача о потоке минимальной стоимости имеет также более общий характер, чем задача поиска кратчайшего пути, согласно следующему простому сведению.
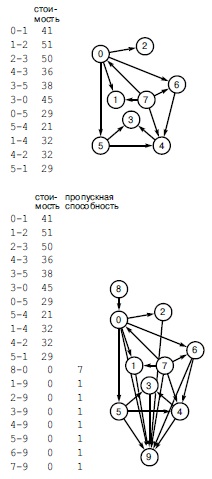
Поиск дерева кратчайших путей из одного истока в сети, изображенной вверху, эквивалентно решению задачи о максимальном потоке минимальной стоимости в транспортной сети, показанной внизу.
Лемма 22.29. Задача о кратчайших путях из одного истока (в сетях без отрицательных циклов) сводится к задаче о допустимом потоке минимальной стоимости.
Доказательство. Пусть имеется задача поиска кратчайших путей из одного истока (сеть с истоком в вершине s). Построим транспортную сеть с теми же вершинами, ребрами и стоимостями ребер и назначим ребрам неограниченную пропускную способность. Добавим новый исток с ребром, которое ведет в s и имеет нулевую стоимость и пропускную способность V - 1, а также новый сток с ребрами, в который ведут ребра из всех других вершин с нулевыми стоимостями и единичными пропускными способностями. Это построение показано на рис. 22.51.
Решим задачу о допустимом потоке минимальной стоимости для этой сети. При необходимости удалим из решения циклы, чтобы получить решение в виде ос-товного дерева. Это остовное дерево непосредственно соответствует остовному дереву кратчайших путей для исходной сети. Подробное доказательство этого факта оставляем читателям в качестве упражнения (см. упражнение 22.138). 
Таким образом, все задачи, рассмотренные в "Кратчайшие пути" , которые сводятся к задаче кратчайших путей из одного истока, также сводятся к задаче о потоке минимальной стоимости. Это множество задач, в частности, включает задачу календарного планирования работ с конечными сроками и с разностными ограничениями.
Как мы убедились при изучении задач о максимальном потоке, имеет смысл проанализировать детали работы сетевого симплексного алгоритма при решении задачи поиска кратчайших путей с помощью сведения, описанного в лемме 22.29. В этом случае алгоритм использует остовное дерево с корнем в истоке - примерно как алгоритмы на основе поиска, которые были рассмотрены в главе 21 "Кратчайшие пути" - но потенциалы и приведенные стоимости увеличивают гибкость при разработке методов выбора следующего ребра для включения в дерево.
Обычно мы не используем тот факт, что задача о потоке минимальной стоимости является естественным обобщением и задачи о максимальном потоке, и задачи поиска кратчайших путей, т.к. для обеих этих задач существуют специальные алгоритмы, гарантирующие более высокую производительность. Однако если таких реализаций нет, то качественная реализация сетевого симплексного алгоритма вполне может обеспечить быстрое решение конкретных экземпляров обеих задач. Разумеется, при использовании или построении систем обработки сетей, в которых применяются такие сведения, следует избегать циклов сведения. Например, реализация алгоритма вычеркивания циклов в программе 22.9 использует для решения задачи о потоке минимальной стоимости как алгоритмы вычисления максимального потока, так и алгоритмы поиска кратчайших путей (см. упражнение 21.96).
Теперь мы рассмотрим несколько эквивалентных сетевых моделей. Вначале покажем, что предположение о неотрицательности стоимостей не ограничивает возможность сведения, т.к. сети с отрицательными стоимостями можно преобразовать в сеть без таковых.
Лемма 22.30. В задачах о потоке минимальной стоимости без потери общности можно считать, что стоимости ребер неотрицательны.
Доказательство. Мы докажем это утверждение для допустимых потоков минимальной стоимости в распределительных сетях. Это результат верен и для максимальных потоков минимальной стоимости в силу эквивалентности этих двух задач согласно лемме 22.22 (см. упражнения 22.143 и 22.144).
Пусть имеется некоторая распределительная сеть. Заменим любое ребро u-v, имеющее стоимость x < 0 и пропускную способность с, на ребро v-u с той же пропускной способностью, но со стоимостью -х (положительной). Теперь можно уменьшить на с значение предложения-спроса вершины u и увеличить на с значение предложения-спроса вершины v. Эта операция соответствует проталкиванию с единиц потока из u в v с соответствующей подстройкой сети.
Если в случае ребер с отрицательной стоимостью решение задачи о потоке минимальной стоимости для преобразованной сети помещает в ребро v-u поток f, то мы помещаем в ребро u-v исходной сети поток с -f. В случае ребер с положительной стоимостью преобразованная сеть содержит те же потоки, что и исходная. Такое распределение потоков сохраняет ограничения на предложение и спрос во всех вершинах.
Поток в ребре u-v преобразованной сети добавляет к стоимости величину fx, а поток в ребре v-u исходной сети - величину - сх + fx. Первый член этого выражения не зависит от потока, значит, стоимость любого потока в преобразованной сети равна стоимости соответствующего потока в исходной сети плюс сумма произведений пропускных способностей на стоимости всех ребер с отрицательными стоимостями (отрицательная величина). Поэтому любой поток минимальной стоимости в преобразованной сети является потоком минимальной стоимости в исходной сети. 
Это сведение показывает, что можно рассматривать только положительные стоимости, хотя на практике мы обычно так не делаем, т.к. наши реализации из разделов 22.5 и 22.6 имеют дело исключительно с остаточными сетями и без проблем обрабатывают отрицательные стоимости. Иногда важно иметь какую-то нижнюю границу стоимостей, но эта граница не должна быть нулевой (см. упражнение 22.145).
Далее мы покажем, что, как и в случае задачи о максимальном потоке, при желании можно ограничиться рассмотрением ациклических сетей. Более того, можно также считать, что ребра не имеют пропускных способностей (не существует верхней границы для величины потока в таких ребрах). Сочетание этих двух вариантов приводит к следующей классической формулировке задачи о потоке минимальной стоимости.
Транспортная задача. Нужно решить задачу о потоке минимальной стоимости для двудольной распределительной сети, все ребра которой направлены из вершины с предложением в вершину со спросом и имеют неограниченную пропускную способность. Как было сказано в начале данной главы (см. рис. 22.2), обычно эта задача моделирует распределение товаров из складов (вершины с предложением) в торговые точки (вершины со спросом) по каналам распределения (ребра) с конкретной стоимостью доставки единицы товара.
Лемма 22.31. Транспортная задача эквивалентна задаче о потоке минимальной стоимости.
Доказательство. Пусть имеется некоторая транспортная задача. Ее можно решить, назначив каждому ребру пропускную способность, более высокую, чем значения предложения или спроса в вершинах этог ребра, и решив полученную задачу нахождения допустимого потока минимальной стоимости для полученной распределительной сети. Значит, остается лишь доказать сводимость стандартной задачи к транспортной задаче.
Для разнообразия опишем новое преобразование, которое линейно только на разреженных сетях. Построение, подобное использованному при доказательстве леммы 22.16, доказывает этот результат и для не разреженных сетей (см. упражнение 22.148).
Пусть имеется стандартная распределительная сеть с V вершинами и E ребрами. Построим транспортную сеть с V вершинами предложения, E вершинами спроса и 2E ребрами следующим образом. Для каждой вершины исходной сети включим в двудольную сеть вершину с величиной предложения или спроса, равной исходному значению плюс сумма пропускных способностей исходящих ребер. А для каждого ребра u-v исходной сети с пропускной способностью c включим в двудольную сеть вершину с величиной предложения или спроса - c (обозначим эту вершину как [u-v]). Для каждого ребра u-v в исходной сети включим в двудольную сеть два ребра: одно с той же стоимостью и ведет из u в [u-v], а другое с нулевой стоимостью и ведет из v в [u-v].
Следующее взаимно однозначное соответствие сохраняет стоимости потоков в обеих сетях неизменными: ребро u-v исходной сети содержит поток величины f тогда и только тогда, когда ребро u-[u-v] содержит поток величины f, а ребро v-[u-v] двудольной сети содержит поток величины c -f (в силу ограничения на предложение-спрос в вершине [u-v] эти два потока должны давать в сумме значение c). Следовательно, любой поток минимальной стоимости в одной сети соответствует потоку минимальной стоимости в другой сети. 
Поскольку мы не рассматривали прямые алгоритмы решения транспортной задачи, это сведение представляет собой лишь академический интерес. Чтобы воспользоваться им, необходимо преобразовать полученную задачу к (другой) задаче вычисления потока минимальной стоимости, воспользовавшись простым сведением, упомянутым в начале доказательства леммы 22.31. Возможно, на практике такие сети допускают более эффективные решения, а возможно, и нет. Цель изучения эквивалентности транспортной задачи и задачи о потоке минимальной стоимости в том, чтобы уяснить, что отказ от пропускных способностей и ограничение двудольными сетями не может существенно упростить задачу вычисления потока минимальной стоимости, как это может показаться.
В этом контексте нам придется рассмотреть другую классическую задачу. Она обобщает задачу о двудольном сопоставлении, которая подробно рассмотрена в разделе 22.4, и так же обманчиво проста.
Задача о назначениях. Для заданного взвешенного двудольного графа нужно найти множество ребер минимальной общей стоимости, чтобы каждая вершина была соединена в точности с одной другой вершиной.
Например, можно обобщить рассмотренную ранее задачу о трудоустройстве, если добавить возможность количественной оценки желания компании заполучить каждого претендента на рабочее место (скажем, присваивая каждому претенденту целочисленные баллы, при этом лучшим претендентам присваиваются более низкие баллы) и количественной оценки желания претендента получить рабочее место в каждой компании. Тогда решение задачи о назначениях предлагает способ разумного учета предпочтений обеих сторон.
Лемма 22.32. Задача о назначениях сводится к задаче вычисления потока минимальной стоимости.
Доказательство. Это утверждение можно доказать простым сведением к транспортной задаче. Пусть имеется задача о назначениях, и нужно построить транспортную задачу с теми же вершинами и ребрами. При этом все вершины из одного множества считаются вершинами с предложением и значением 1, а все вершины из другого множества считаются вершинами со спросом и значением 1. Назначим каждому ребру единичную пропускную способность и стоимость, соответствующую весу этого ребра в задаче о назначениях. Любое решение этого экземпляра транспортной задачи - это просто множество ребер минимальной общей стоимости, где каждое ребро соединяет вершину с предложением с вершиной со спросом, то есть оно непосредственно соответствует решению исходной задачи о назначениях.
Сведение этого экземпляра транспортной задачи к задаче вычисления минимального потока минимальной стоимости дает построение, по существу эквивалентное построению, которое мы использовали для сведения задачи двудольного сопоставления к задаче вычисления максимального потока (см. упражнение 22.158). 
Это отношение не является эквивалентностью, поскольку способ сведения общей задачи о потоке минимальной стоимости к задаче о назначениях пока не известен. Аналогично задаче поиска кратчайших путей из одного истока и задаче вычисления максимального потока, задача о назначениях кажется более легкой для решения, чем задача вычисления потока минимальной стоимости: ведь алгоритмы ее решения имеют более высокую асимптотическую производительность, чем лучшие известные алгоритмы для задачи вычисления потока минимальной стоимости. Однако сетевой симплексный алгоритм настолько отлажен, что хорошая программная реализация вполне годится для решения задачи о назначениях. Более того, как и в задачах поиска максимального потока и кратчайших путей, можно приспособить сетевой симплексный алгоритм для более эффективного решения задачи о назначениях (см. раздел ссылок).
Следующее сведение к задаче вычисления потока минимальной стоимости возвращает нас к базовой задаче поиска путей в графах, вроде тех, которые были впервые рассмотрены в "Виды графов и их свойства" . Как и в случае задачи вычисления эйлерова пути, нужно найти путь, который содержит все ребра графа. Но поскольку не все графы содержат такой путь, мы ослабляем ограничение, требующее, чтобы каждое ребро входило в путь только один раз.
Задача о почтальоне. Пусть имеется некоторая сеть (взвешенный орграф), и нужно найти замкнутый путь минимального веса, содержащий каждое ребро не менее одного раза (см. рис. 22.52). Напомним, что основные определения в "Виды графов и их свойства" различают циклические пути (которые могут неоднократно проходить по вершинам и ребрам) и циклы (состоящие из различных вершин, за исключением совпадающих первой и последней).
Поиск кратчайшего пути, который включает каждое ребро по меньшей мере один раз - трудная задача даже для такой простой сети, но она эффективно решается с помощью сведения к задаче о потоке минимальной стоимости.
Решение этой задачи описывает наилучший маршрут почтальона (который должен пройти все улицы на своем пути). Решение этой задачи может также описывать маршрут снегоочистителя во время метели; существует и множество других аналогичных применений.
Задача о почтальоне представляет собой расширение задачи поиска эйлерова цикла, рассмотренной в "Виды графов и их свойства" : решение упражнения 17.92 дает простую проверку на существование в орграфе эйлерова пути, а программа 17.14 является эффективным способом поиска эйлерова цикла в таких орграфах. Этот путь решает задачу о почтальоне, т.к. он содержит каждое ребро в точности один раз - никакой другой путь не может иметь более низкий вес. Задача усложняется, если степени захода и выхода не обязательно равны. В общем случае некоторые ребра приходится проходить более одного раза, и тогда задача заключается в том, чтобы минимизировать общий вес многократно посещаемых ребер.
Лемма 22.33. Задача о почтальоне сводится к задаче вычисления потока минимальной стоимости.
Доказательство. Пусть имеется экземпляр задачи о почтальоне (взвешенный орграф). Нужно определить распределительную сеть с теми же вершинами и ребрами, где значения предложения и спроса во всех вершинах равны 0, стоимости ребер равны весам соответствующих ребер, пропускные способности ребер не ограничены сверху, но все пропускные способности ребер должны быть больше 1. Величина f потока в ребре u-v означает, что всего почтальон должен пройти f раз по ребру u-v.
Найдем поток минимальной стоимости для этой сети, воспользовавшись преобразованием, описанным в упражнении 22.146, чтобы снять ограничение снизу на пропускные способности ребер. Теорема разложения потока утверждает, что поток можно представить в виде множества циклов. Значит, из этого потока можно построить циклический путь точно так же, как мы строили эйлеров цикл на эйлеровом графе: проходим по любому циклу, выходя из него для обхода другого цикла всякий раз, когда встречается вершина, принадлежащая другому циклу. 
Тщательный анализ задачи о почтальоне еще раз демонстрирует тонкую грань между тривиальными и трудноразрешимыми задачами в области алгоритмов на графах. Предположим, что мы рассматриваем двунаправленный вариант этой задачи, когда сеть неориентированная, а почтальон должен пройти по каждому ребру в обоих направлениях. Тогда, как было сказано в разделе 18.5 "Поиск на графе" , поиск в глубину (или любой другой поиск на графе) даст нам немедленное решение. Но если достаточно одного прохода по ребру в каком-либо направлении, то решение задачи оказывается намного сложнее, чем просто сведение к задаче о потоке минимальной стоимости, с которым мы только что ознакомились, хотя задача все еще разрешима. Если некоторые ребра ориентированы, а другие нет, задача становится NP-трудной (см. раздел ссылок).
Это лишь немногие из десятков практических задач, которые можно сформулировать в виде задач о потоке минимальной стоимости. Задача о потоке минимальной стоимости более универсальна, чем задача вычисления максимального потока или построения кратчайшего пути, а сетевой симплексный алгоритм эффективно решает все задачи, охватываемые этой моделью.
Так же, как при изучении максимального потока, мы можем выяснить, как представить любую задачу о минимальном потоке в виде LP-задачи (см. рис. 22.53). Ее формулировка является простым расширением формулировки задачи о максимальном потоке: мы добавляем уравнения, в которых фиктивной переменной приравнивается стоимость потока, затем стараемся минимизировать эту переменную. LP-модели позволяют добавить произвольные (линейные) ограничения. Некоторые из этих ограничений могут привести к задачам, все равно эквивалентным задачам о потоках минимальной стоимости, другие - нет. То есть многие задачи не сводятся к задачам о потоках минимальной стоимости: например, линейное программирование охватывает гораздо более широкое множество задач. Задача о потоке минимальной стоимости представляет собой следующий шаг к той обобщенной модели решения задачи, которая будет рассматриваться в части VIII.
Эта линейная программа эквивалентна задаче о максимальном потоке минимальной стоимости для сети с0 рис. 22.40. Равенства для вершин и неравенства для ребер те же, что и на рис.22.39, но цель здесь другая. Переменная c представляет собой общую стоимость, которая является линейной комбинацией других переменных. В данном случае с = -9x50 + x01 + x02 + x13 + x14 + 4x23 + 2x24 + 2x35 + x45 .
Существуют другие модели, которые имеют еще более общий характер, чем LP-модель; однако линейное программирование обладает дополнительным достоинством: хотя LP-задачи в общем случае более сложны, чем задачи о потоке минимальной стоимости, для их решения разработаны эффективные алгоритмы. Возможно, наиболее важный из этих алгоритмов - симплекс-метод, и сетевой симплексный метод представляет собой специализированный вариант симплекс-метода, применимый к подмножеству LP-задач, которые соответствуют задачам о потоке минимальной стоимости. Понимание сетевого симплексного алгоритма облегчает понимание алгоритма симплекс-метода.
Упражнения
22.133. Покажите, что когда сетевой симплексный алгоритм вычисляет максимальный поток, остовное дерево представляет собой объединение ребра t-s, дерева, содержащего вершину s, и дерева, содержащего вершину t.
22.134. Разработайте реализацию, вычисляющую максимальный поток на основе упражнения 22.133. Выбирайте подходящее ребро случайным образом.
22.135. Покажите в стиле рис. 22.50 процесс вычисления максимального потока в транспортной сети, изображенной на рис. 22.10, используя описанное в тексте сведение и реализацию сетевого симплексного алгоритма из программы 22.14.
22.136. Покажите в стиле рис. 22.50 процесс построения кратчайших путей из вершины 0 в транспортной сети, изображенной на рис. 22.10, используя описанное в тексте сведение и реализацию сетевого симплексного алгоритма из программы 22.14.
22.137. Докажите, что все ребра остовного дерева, описанного в доказательстве леммы 22.29, принадлежат путям, ведущим из истока к листьям.
22.138. Докажите, что остовное дерево, описанное в доказательстве леммы 22.29, соответствует дереву кратчайших путей в исходной сети.
22.139. Предположим, что вы используете сетевой симплексный алгоритм для решения задачи, полученной в результате сведения задачи о кратчайших путях из одного истока, как описано в доказательстве леммы 22.29. (1). Докажите, что этот алгоритм никогда не использует расширяющий путь нулевой стоимости. (2) Покажите, что удаляемое из цикла ребро всегда является родителем конечной вершины ребра, добавленного в цикл. (3) Из упражнения 22.138 следует, что сетевой симплексный алгоритм не обязан использовать потоки в ребрах. Представьте полную реализацию, в которой используется этот факт. Выбирайте новое древесное ребро случайным образом.
22.140. Пусть каждое ребро сети имеет положительную стоимость. Докажите, что задача построения дерева кратчайших путей из одного истока минимальной стоимости сводится к задаче о максимальном потоке минимальной стоимости.
22.141. Изменим задачу планирования с конечными сроками из "Кратчайшие пути" так, что работы могут нарушать сроки завершения, если при этом они получают некоторую положительную стоимость. Покажите, что эта модифицированная задача сводится к задаче о максимальном потоке минимальной стоимости.
22.142. Реализуйте класс, который находит максимальные потоки минимальной стоимости в распределительных сетях с отрицательными стоимостями. Воспользуйтесь полученным классом для решения упражнения 22.105 (где все стоимости неотрицательны).
22.143. Пусть стоимости ребер 0-2 и 1-3 на рис. 22.40 равны -1, а не 1. Покажите, как найти максимальный поток минимальной стоимости путем преобразования заданной сети в сеть с положительными стоимостями с последующим вычислением максимального потока минимальной стоимости в новой сети.
22.144. Реализуйте класс, который находит максимальные потоки минимальной стоимости в сетях с отрицательной стоимостью. Воспользуйтесь классом MINCOST (в котором считается, что все стоимости неотрицательны).
22.145. Зависят ли реализации из разделов 22.5 и 22.6 существенным образом от того, что цены неотрицательны? Если зависят, то объясните, как. Если не зависят, покажите, какие нужны (если нужны) изменения, чтобы они работали для сетей с отрицательными стоимостями, либо объясните, почему такие изменения невозможны.
22.146. Добавьте в АТД допустимого потока из упражнения 22.74 возможность указания нижних границ пропускных способностей ребер. Реализуйте класс, который вычисляет максимальный поток минимальной стоимости с учетом этих границ (если он возможен).
22.147. Приведите результат использования сведения транспортной сети, описанной в упражнении 22.112, к транспортной задаче.
22.148. Покажите, что задача о максимальном потоке минимальной стоимости сводится к транспортной задаче со всего лишь V дополнительными вершинами и ребрами, если выполнить построение, аналогичному тому, что приведено в доказательстве леммы 22.16.
22.149. Реализуйте класс для решения транспортной задачи, основанный на простом сведении задачи о потоке минимальной стоимости, описанном в доказательстве леммы 22.30.
22.150. Разработайте реализацию класса для решения задачи вычисления потока минимальной стоимости на основе сведения к транспортной задаче, описанного в доказательстве леммы 22.31.
22.151. Разработайте реализацию класса для решения задачи вычисления потока минимальной стоимости на основе сведения к транспортной задаче, описанного в упражнении 22.148.
22.152. Напишите программу, генерирующую случайные экземпляры транспортной задачи, и используйте их для эмпирических тестов различных алгоритмов и реализаций, решающих эту задачу.
22.153. Найдите в интернете пример крупной транспортной задачи.
22.154. Эмпирически сравните два различных метода сведения произвольных задач о потоках минимальной стоимости к транспортной задаче, которые приведены в доказательстве леммы 22.31.
22.155. Напишите программу, генерирующую случайные экземпляры задачи о назначениях, и используйте их для эмпирических тестов различных алгоритмов и реализаций, решающих эту задачу.
22.156. Найдите в интернете пример крупной задачи о назначениях.
22.157. Задача о трудоустройстве, описанная в тексте, дает большее преимущество работодателям (максимизируется их общий вес). Сформулируйте версию этой задачи, где претенденты на рабочие места также могут высказывать свои пожелания. Объясните, как решить такую задачу.
22.158. Эмпирически сравните производительность двух реализаций сетевого симплексного алгоритма из раздела 22.6 при решении случайных вариантов задачи о назначениях (см. упражнение 22.155) с Vвершинами и E ребрами и разумным выбором значений V и E.
22.159. Понятно, что задача о почтальоне не имеет решения для сетей, которые не являются сильно связными (почтальон может посетить только вершины, содержащиеся в том сильном компоненте, где он начинает свой обход), однако это не оговаривается в сведении, которое описано в лемме 22.33. Что произойдет, если применить сведение к сети, которая не является сильно связной?
22.160. Эмпирические определите среднюю длину пути почтальона для различных взвешенных графов (см. упражнения 21.4-21.8).
22.161. Приведите прямое доказательство того, что задача о кратчайшем пути из одного истока сводится к задаче о назначениях.
22.162. Приведите формулировку произвольной задачи о назначениях в виде LP-задачи.
22.163. Выполните упражнение 22.18 для случая, когда стоимость каждого ребра равна - 1 (чтобы свести к минимуму пустое место в грузовых машинах).
22.164. Найдите такую модель стоимостей для упражнения 22.18, чтобы ее решением был максимальный поток, требующий минимальное количество дней.