|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Потоки в сетях
Алгоритмы определения максимальных потоков проталкиванием напора
В этом разделе мы рассмотрим другой способ решения задачи о максимальном потоке. Используя обобщенный метод, который называется методом проталкивания напора (preflow-push), мы будем постепенно проталкивать поток по ребрам, исходящим из вершин, в которых приток превышает отток. Метод проталкивания напора был разработан Гольдбергом (A. Goldberg) и Тарьяном (R.E.Tarjan) в 1986 г. на основе различных уже известных алгоритмов и получил широкое распространение благодаря своей простоте, гибкости и эффективности.
Как сказано в разделе 22.1, поток должен удовлетворять условию баланса: отток из истока должен быть равен притоку в сток, а в каждом внутреннем узле приток равен оттоку. Мы называем такой поток допустимым (feasible) потоком. Алгоритм расширения путей всегда поддерживает допустимость потока, наращивая поток вдоль расширяющих путей, пока не будет достигнут максимальный поток. В отличие от этого, алгоритмы проталкивания напора, которые будут рассмотрены в этом разделе, работают с не допустимыми потоками, и в некоторых вершинах приток может превышать отток: они проталкивают поток через эти вершины, пока поток не станет допустимым (когда не останется таких вершин).
Определение 22.5. Напор (preflow) в транспортных сетях - это множество положительных потоков в ребрах, удовлетворяющих условиям: поток в каждом ребре не превосходит пропускную способность этого ребра, и приток в каждой внутренней вершине не меньше оттока. Активная (active) вершина - это внутренняя вершина, приток в которой больше оттока (по соглашению исток и сток не считаются активными).
Разность между притоком и оттоком активной вершины называется ее избытком (excess). Чтобы изменить множество активных вершин, мы выбираем одну из них и проталкиваем (push) ее избыток в исходящее ребро, а если пропускной способности этого ребра не хватает, то избыток выталкивается назад по входящему ребру. Если проталкивание балансирует приток и отток, вершина перестает быть активной; поток, протолкнутый в другую вершину, может активировать ее. Метод проталкивания напора представляет собой систематический способ многократного выталкивания избытка из активных вершин; по окончании процесса получается максимальный поток, и нет активных вершин. Активные вершины содержатся в обобщенной очереди. Это решение позволяет получить обобщенный алгоритм, который охватывает целое семейство специальных алгоритмов.
На рис. 22.25 приведен небольшой пример базовых операций, используемых методом проталкивания напора, где предполагается, что поток может идти только вниз. Мы либо проталкиваем избыточный поток из активной вершины вниз по исходящему ребру, либо воображаем, что активная вершина временно перемещается вверх, и мы можем протолкнуть избыточный поток как бы вниз по входящему ребру.
В алгоритме проталкивания напора используется список активных узлов, в которых входящие потоки больше исходящих (показаны под каждой диаграммой сети). Одна из версий алгоритма представляет собой цикл, который выбирает из этого списка активный узел и проталкивает поток по исходящим ребрам, пока узел не перестанет быть активным. При этом возможно появление других активных узлов. В данном примере мы проталкиваем поток по ребру 0-1, после чего узел 1 становится активным. После этого мы проталкиваем поток по ребрам 1-2 и 1-3, и узел 1 перестает быть активным, зато активируются узлы 2 и 3. Затем мы проталкиваем поток по ребру 2-4, и 2 становится неактивным узлом. Однако пропускной способности ребра 3-4 недостаточно, чтобы протолкнуть поток по нему и сделать узел 3 неактивным, поэтому поток проталкивается по ребру 3-1 обратно в вершину 1, которая снова активируется. Теперь можно протолкнуть поток по ребру 1-2, а затем по 2-4, после чего все узлы становятся неактивными, и мы получаем максимальный поток.
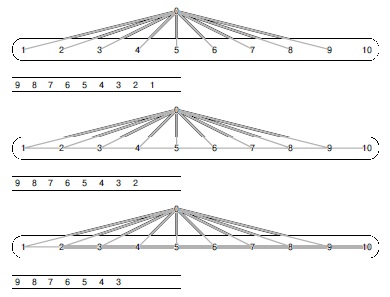
На рис. 22.26 показан пример, который показывает, почему метод проталкивания напора может оказаться лучше метода расширения путей. В рассматриваемой сети любой метод расширения путей многократно добавляет в длинный путь крошечные порции потока, медленно наполняя ребра этого пути, пока не будет достигнут максимальный поток. В отличие от этого, метод проталкивания напора заполняет ребра этого длинного пути при первом проходе по нему, а затем распределяет этот поток непосредственно в сток без повторного прохода по длинному пути.
Как и в случае алгоритмов с использованием расширяющих путей, мы используем остаточные сети (см. определение 22.4), чтобы выявлять ребра, через которые можно проталкивать поток. Каждое ребро остаточной сети представляет собой потенциальное место, где можно протолкнуть поток. Если ребро остаточной сети имеет то же направление, что и соответствующее ребро транспортной сети, мы увеличиваем поток, а если противоположное, то уменьшаем. Если увеличение потока заполняет ребро или уменьшение потока опустошает ребро, то соответствующее ребро исчезает из остаточной сети. В алгоритмах проталкивания напора мы используем дополнительный механизм, который позволяет решить, какие ребра в остаточной сети помогут устранить активные вершины.
Эта сеть представляет семейство сетей с V вершинами, для которых любой алгоритм расширения путей требует V/2 путей длиной V/2 (поскольку каждый расширяющий путь должен содержать длинный вертикальный путь), а для этого потребуется время, пропорциональное V2. Алгоритмы проталкивания напора находят максимальный поток в таких сетях за линейное время.
Определение 22.6. Функция высоты (height function) для данного потока в транспортной сети - это множество неотрицательных весов вершин h(0) ... h(V - 1), такое, что h(t) = 0 для стока t, и 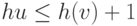 для каждого ребра u-v из остаточной сети этого потока. Подходящее ребро (eligible edge) - это такое ребро u-v остаточной сети, что h(u) = h(v) + 1.
для каждого ребра u-v из остаточной сети этого потока. Подходящее ребро (eligible edge) - это такое ребро u-v остаточной сети, что h(u) = h(v) + 1.
Тривиальная функция высоты, для которой не существует подходящих ребер, имеет вид h(0) = h(1) = ... = h(V - 1) = 0. Если задать h(s) = 1, то любое ребро, исходящее из истока и содержащее поток, соответствует подходящему ребру в остаточной сети.
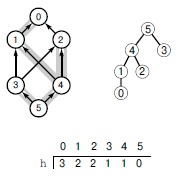
Можно дать более интересное определение функции высоты, присвоив каждой вершине длину кратчайшего пути от нее до стока (расстояние до корня в любом дереве BFS для обратной сети с корнем в t - см. рис. 22.27). Эта функция высоты верна потому, что h(t) = 0, и для любой пары вершин u и v, соединенных ребром u-v, любой кратчайший путь, ведущий в t и начинающийся ребром u-v, имеет длину h(v) + 1; таким образом, длина кратчайшего пути из u в t, т.е. h(u), должна быть меньше или равна этому значению. Эта функция играет особую роль, т.к. она помещает каждую вершину на максимально возможную высоту. Обратные рассуждения показывают, что вершина t должна находиться на высоте 0; единственными вершинами, которые могут находиться на высоте 1, являются вершины, которым соответствуют ребра, направленные в t в остаточной сети; на высоте 2 могут находиться только вершины, ребра из которых направлены в вершины, которые могут быть на высоте 1 и т.д.
Справа изображено дерево BFS с корнем в вершине 5 обращения сети, приведенной слева. Массив h, индексированный именами вершин, содержит расстояние от каждой вершины сети до корня и представляет собой адекватную функцию высоты: для каждого ребра u-v сети значение h[u] меньше или равно h[v]+1.
Лемма 22.9. Для любого потока и связанной с ним функции высоты высота любой вершины не превосходит длины кратчайшего пути из этой вершины в сток в остаточной сети.
Доказательство. Пусть для любой заданной вершины u значение d есть длина кратчайшего пути из u в t, и пусть u = u1, u2, ..., ud = t - кратчайший путь. Тогда
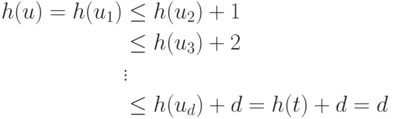

Смысл функции высоты в следующем: если высота активного узла меньше, чем высота истока, то, возможно, можно как-то протолкнуть поток из этого узла в сток; если высота активного узла больше, чем высота истока, нужно избыток этого узла вытолкнуть обратно в исток. Чтобы обосновать последний факт, мы изменим направление леммы 22.9, где длина кратчайшего пути выступает в качестве верхней границы высоты; вместо этого будем рассматривать высоту как нижнюю границу длины кратчайшего пути.
Следствие. Если высота вершины больше V, то в остаточной сети не существует пути из этой вершины в сток.
Доказательство. Если существует путь из этой вершины в сток, то из леммы 22.9 следует, что длина пути будет больше V, но этого не может быть, т.к. в сети имеется всего V вершин. 
Теперь, когда мы понимаем эти базовые механизмы, нетрудно описать обобщенный алгоритм проталкивания напора. Мы начнем с любой функции высоты и назначим нулевой поток всем ребрам, за исключением исходящих из истока, которые заполним до пропускной способности. Затем будем повторять следующее действие до тех пор, пока не останется активных вершин:
Выбираем активную вершину. Проталкиваем поток через некоторое подходящее ребро, исходящее из этой вершины (если оно есть). Если таких ребер нет, увеличиваем на 1 высоту вершины.
Мы не конкретизируем, как выглядит исходная функция высоты, как выбирается активная вершина, как выбирается подходящее ребро или какая величина потока выталкивается. Мы будем называть этот обобщенный метод как реберный (edge-based) алгоритм проталкивания напора.
Этот алгоритм зависит от выбора функции высоты, позволяющей находить подходящие ребра. Мы также используем функцию высоты как для доказательства того, что этот алгоритм вычисляет максимальный поток, так и для анализа производительности. Поэтому необходимо обеспечить, чтобы функция высоты оставалась адекватной на протяжении всей работы алгоритма.
Лемма 22.10. Реберный алгоритм проталкивания напора сохраняет адекватность функции высоты.
Доказательство. Мы увеличиваем значение h(u) только при отсутствии таких ребер u-v, что h(u) = h(v) + 1. То есть до увеличения h(u) для всех ребер u-v справедливо h(u) < h(v) + 1, а после него справедливо 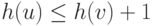 . Для любого входящего ребра w-u увеличение h(u) на 1 наверняка сохранит справедливость неравенства
. Для любого входящего ребра w-u увеличение h(u) на 1 наверняка сохранит справедливость неравенства 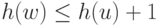 . Увеличение h(u) не влияет на неравенства для любых других ребер, и мы никогда не увеличиваем h(t) (или h(s)). Из этих двух наблюдений следует результат.
. Увеличение h(u) не влияет на неравенства для любых других ребер, и мы никогда не увеличиваем h(t) (или h(s)). Из этих двух наблюдений следует результат. 
Весь излишек потока берет начало в истоке. Образно говоря, обобщенный алгоритм проталкивания напора пытается протолкнуть избыточный поток в сток, а если это ему не удается, он проталкивает избыточный поток обратно в исток. Он работает так потому, что узлы с избытком всегда остаются связанными с истоком в остаточной сети.
Лемма 22.11. Во время выполнения алгоритма проталкивания напора на транспортной сети существует (ориентированный) путь в соответствующей остаточной сети из каждой активной вершины в исток, и не существуют (ориентированные) пути из истока в сток остаточной сети.
Доказательство. Выполняется методом индукции. Вначале поток протекает только по ребрам, исходящим из истока, которые заполнены до их пропускной способности, так что активными вершинами в сети являются только конечные вершины этих ребер. Поскольку эти ребра заполнены до пропускной способности, в остаточной сети существует ребро, ведущее из каждой из этих вершин в исток, но там нет ребер, исходящих из истока. Поэтому указанное свойство справедливо для первоначального потока.
Исток достижим из любой активной вершины, т.к. единственный способ увеличения множества активных вершин состоит в проталкивании потока из активной вершины вниз по подходящему ребру. По индуктивному предположению эта операция оставляет в остаточной сети ребро, ведущее из принимающей вершины в активную вершину, из которой достижим исток.
Вначале никакой другой узел остаточной сети не доступен из истока. Впервые некоторый узел u становится доступным из истока тогда, когда поток выталкивается в обратном направлении по ребру u-s (из-за чего в остаточную сеть добавляется ребро s-u). Но это возможно только когда h(u) больше h(s), а это может случиться только после увеличения h(u), т.к. в остаточной сети нет ребер, ведущих в вершины с меньшей высотой. Аналогичное рассуждение показывает, что все узлы, достижимые из истока, имеют большую высоту. Но поскольку высота стока всегда равна 0, он не может быть достижим из истока. 
Следствие. Во время выполнения алгоритма проталкивания напора высоты вершин всегда меньше 2V.
Доказательство. Достаточно рассмотреть только активные вершины, поскольку высота неактивных вершин либо имеет то же значение, либо на 1 больше значения, которое вершина имела, когда последний раз была активной. Такие же рассуждения, как и в доказательстве леммы 22.9 показывают, что из наличия пути из заданной активной вершины в исток следует, что высота этой вершины максимум на V- 2 больше высоты истока (этот путь не может проходить через t ). Высота истока никогда не меняется и первоначально не может быть больше V. Следовательно, высота активных вершин не может превышать значения 2V- 2, и ни одна из вершин не может иметь высоту 2V или больше. 
Обобщенный алгоритм проталкивания напора легко сформулировать и реализовать. Возможно, пока непонятно, почему он вычисляет максимальный поток. Функция высоты - ключевой фактор, позволяющий доказать это.
Лемма 22.12. Алгоритм проталкивания напора вычисляет максимальный поток.
Доказательство. Вначале нужно доказать, что алгоритм однажды останавливается. Должен наступить момент, когда не останется ни одной активной вершины. Как только мы вытолкнем весь избыточный поток из некоторой вершины, эта вершина не может снова стать активной, пока какая-то часть этого потока не будет вытолкнута назад, а это может случиться только при увеличении высоты этой вершины. Если имеется последовательность активных вершин неограниченной длины, хотя бы одна из вершин должна появиться в этой последовательности неограниченное число раз, а это может случиться только при неограниченном возрастании ее высоты, что противоречит лемме 22.9.
Если активных вершин нет, то поток допустим. А поскольку, согласно лемме 22.11, в остаточной сети пути из истока в сток нет, то рассуждения, использованные в доказательстве леммы 22.5, показывают, что поток в сети является максимальным. 
Можно уточнить доказательство обязательного завершения алгоритма и получить границу времени выполнения в худшем случае O(V2E ). Детали этого доказательства мы оставляем читателям на самостоятельную проработку (см. упражнения 22.66 и 22.67), а здесь отдадим предпочтение более простому доказательству леммы 22.13, которое относится к более специальной версии алгоритма. А именно, рассматриваемые нами реализации будут основаны на более конкретных повторяющихся инструкциях:
Выбираем активную вершину. Увеличиваем поток в подходящем ребре, исходящем из этой вершины (по возможности заполняем его), и продолжаем так, пока вершина не перестанет быть активной или не останется подходящих ребер. В последнем случае увеличиваем высоту вершины.
То есть после выбора вершины мы выталкиваем из нее как можно больший поток. Если в вершине все равно останется избыток потока, но не останется подходящих ребер, мы увеличиваем на 1 высоту этой вершины. Мы будем называть этот метод вершинным (vertex-based) алгоритмом проталкивания напора. Это специальный случай реберного обобщенного алгоритма, где одна и та же вершина выбирается до тех пор, пока она не перестанет быть активной, либо пока не будут использованы все подходящие ребра, исходящие из нее. Доказательство леммы 22.12 верно для любой реализации реберного обобщенного алгоритма, а это значит, что вершинный алгоритм вычисляет максимальный поток.
Программа 22.5 представляет собой реализацию обобщенного вершинного алгоритма, который использует обобщенную очередь для хранения активных вершин. Эта непосредственная реализация только что описанного метода представляет собой семейство алгоритмов, которые отличаются только исходными функциями высоты (см. например, упражнение 22.52) и реализацией АТД обобщенной очереди. В ней предполагается, что обобщенная очередь отбрасывает повторяющиеся вершины; в противном случае в программу 22.5 можно добавить код, запрещающий занесение дубликатов в очередь (см. упражнения 22.61 и 22.62).
Программа 22.5. Реализация вычисления максимального потока методом проталкивания напора
В данной реализации обобщенного вершинного алгоритма проталкивания напора для вычисления максимального потока используется обобщенная очередь, которая не принимает дубликаты активных вершин. Вектор wt содержит избыточный поток каждой вершины и таким образом неявно определяет множество активных вершин. Здесь вершина s первоначально активна, но никогда не возвращается в очередь, а t никогда не бывает активной. Основной цикл выбирает активную вершину v, затем проталкивает поток через каждое из его подходящих ребер (и при необходимости заносит вершины, принимающие потоки, в список активных вершин) до тех пор, пока либо v станет неактивной, либо будут перебраны все подходящие ребра. В последнем случае высота v увеличивается, а сама она возвращается в очередь.
template <class Graph, class Edge>
class MAXFLOW
{ const Graph &G;
int s, t;
vector<int> h, wt;
void initheights();
public:
MAXFLOW(const Graph &G, int s, int t) : G(G),
s(s), t(t), h(G.V()), wt(G.V(), 0)
{ initheights();
GQ gQ(G.V());
gQ.put(s); wt[t] = -(wt[s] = M*G.V());
while (!gQ.empty())
{ int v = gQ.get();
typename Graph::adjIterator A(G, v);
for (Edge* e = A.beg(); !A.end(); e = A.nxt())
{ int w = e->other(v);
int cap = e->capRto(w);
int P = cap < wt[v] ? cap : wt[v];
if (P > 0 && v == s || h[v] == h[w]+1)
{ e->addflowRto(w, P);
wt[v] -= P; wt[w] += P;
if ((w != s) && (w != t)) gQ.put(w);
}
}
if (v != s && v != t && wt[v] > 0)
{ h[v]+ + ; gQ.put(v); }
}
}
} ;
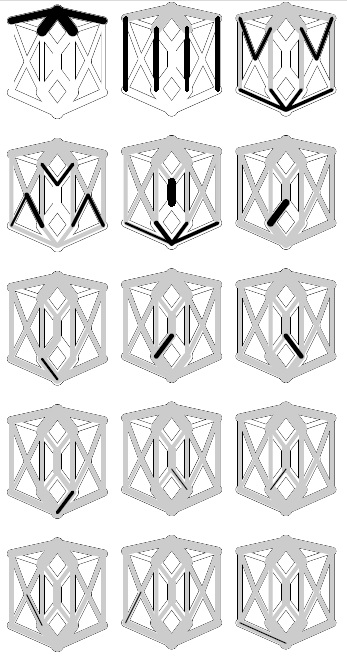
Пожалуй, наиболее простой структурой данных для хранения активных вершин является очередь FIFO. На рис. 22.28 рис. 22.28 показана работа этого алгоритма на демонстрационной сети. Из рисунка видно, что последовательность активных вершин удобно разбить на последовательность этапов. Этап - содержимое очереди после обработки всех вершин из предыдущего этапа. Это помогает ограничить общее время выполнения алгоритма.
Лемма 22.13. Время выполнения реализации алгоритма проталкивания напора на базе очереди FIFO в худшем случае пропорционально V2E .
Доказательство. Мы ограничим количество этапов, воспользовавшись для этой цели функцией потенциала. Наши рассуждения представляют собой простой пример применения мощной технологии анализа алгоритмов и структур данных, которые будут более подробно рассмотрены в части 8.
Определим величину ф равной 0, если в сети нет активных вершин, и равной максимальной высоте активных вершин в противном случае. Теперь рассмотрим, как влияет каждый этап на величину ф. Пусть h0(s) - начальная высота истока. Вначале ф = h0(s) , а в конце ф = 0.
Прежде всего отметим, что количество этапов, в которых высота некоторых вершин возрастает, не превосходит значения 2V2 - h0(s) , поскольку, согласно следствию из леммы 22.11, высоту каждой из V вершин можно увеличить не более чем до 2V . Поскольку ф может возрастать только при увеличении высоты каких-либо вершин, количество этапов, при которых ф возрастает, не может быть больше, чем 2V2 - h0(s) .
А если на каком-то этапе высота ни одной из вершин не увеличена, то значение ф должно быть уменьшено не менее чем на 1, поскольку этап проталкивает весь избыточный поток из каждой активной вершины в вершины с меньшей высотой. Из всех этих фактов следует, что количество этапов не должно быть больше 4V2 : значение ф вначале равно h0(s) и может быть увеличено максимум 2V2 - h0(s) раз, т.е. оно может быть уменьшено максимум 2V2 раз. Худший случай для каждого этапа возникает, когда все вершины находятся в очереди, и все ребра просмотрены, что и дает сформулированную границу для общего времени выполнения.
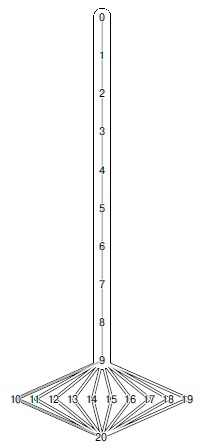
Эта граница жесткая. На рис. 22.29
рис.
22.29 изображено семейство транспортных сетей, для которых количество этапов, использованных алгоритмом проталкивания напора, пропорционально V2. 
Поскольку наши реализации используют неявное представление остаточной сети, они просматривают ребра, исходящие из вершины, даже если их нет в остаточной сети (чтобы проверить, находятся они там или нет). Можно показать, что границу V2E из леммы 22.13 можно снизить до V3, если использовать реализацию, в которой используется явное представление остаточной сети. Хотя эта теоретическая граница - наименьшая из тех, с которыми нам приходилось сталкиваться для задачи вычисления максимального потока, она вряд ли заслуживает нашего внимания, особенно для разреженных графов, которые часто встречаются на практике (см. 22.63-22.65).
Как обычно, границы для худшего случая слишком осторожны и поэтому редко пригодны для прогнозирования производительности алгоритма на реальных сетях (хотя разница и не так велика, как в случае алгоритмов с использованием расширяющих путей). Например, алгоритм FIFO находит поток в сети, представленной на рис. 22.30, за 15 этапов, а оценка из леммы 22.13 утверждает лишь, что количество этапов не превышает 182.
На этом рисунке показаны транспортные сети (слева) и остаточные сети (справа) для каждого этапа алгоритма проталкивания напора на базе очереди FIFO. Содержимое очередей показано под диаграммами транспортных сетей, а метки расстояний - под диаграммами остаточных сетей. На начальном этапе мы проталкиваем поток по ребрам 0-1 и 0-2, что делает вершины 1 и 2 активными. На втором этапе мы проталкиваем поток через эти две вершины в 3 и 4, после чего они становятся активными, а вершина 1 перестает быть активной (вершина 2 остается активной, а метка ее расстояния увеличивается). На третьем этапе мы проталкиваем поток через вершины 3 и 4 в вершину 5, что делает их неактивными (вершина 2 все еще активна, а ее метка расстояния снова увеличивается). На четвертом этапе 2 остается единственным активным узлом, а ребро 2-0 становится приемлемым из-за увеличения метки расстояния, и одна единица потока проталкивается обратно по ребру 2-0, после чего вычисление завершается.
Данная сеть представляет семейство сетей с Vвер-шинами, на которых общее время работы алгоритма проталкивания напора пропорционально V2. Она состоит из ребер с единичной пропускной способностью, исходящих из истока (вершина 0), и горизонтальных ребер с пропускной способностью v - 2, ведущих слева направо в сторону стока (вершина 10). На начальном этапе алгоритма проталкивания напора (вверху) мы проталкиваем одну единицу потока из каждого ребра, ведущего из истока, после чего становятся активными все вершины, кроме истока и стока. В стандартном представлении списками смежности они попадают в очередь FIFO активных вершин в обратном порядке, как показано в строке под диаграммой сети. На втором этапе (в центре) мы выталкиваем единицу потока из 9 в 10, сделав (временно) 9 неактивной; затем выталкиваем единицу потока из 8 в 9, сделав 8 (временно) неактивной, а 9 активной; затем выталкиваем единицу потока из вершины 7 в 8, сделав 7 (временно) неактивной, а 8 активной и т.д. Только вершина 1 остается неактивной. На третьем этапе (внизу) мы выполняем аналогичный процесс, чтобы сделать неактивной вершину 2. Этот процесс продолжается на протяжении V- 2 этапов.
Чтобы повысить производительность, можно попробовать использовать в программе 22.5 стек, рандомизированную очередь или любой другой вид обобщенной очереди. Один из подходов, хорошо зарекомендовавших себя на практике, заключается в такой реализации обобщенной очереди, чтобы функция GQGet возвращала максимальную активную вершину. Мы будем называть этот метод алгоритмом вычисления максимального потока методом проталкивания напора из вершины с максимальной высотой (highest-vertex-preflow-push). Эту стратегию можно реализовать с помощью очереди с приоритетами, но если воспользоваться конкретными особенностями высот, то можно обеспечить выполнение операций на обобщенной очереди за постоянное время. Было доказано, что граница времени выполнения этого алгоритма в худшем случае равна 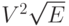 (для разреженных графов
V5/2
) (см. раздел ссылок). Как обычно, эта оценка слишком осторожна. Было предложено и множество других вариантов проталкивания напора, и некоторые из них понижают границу времени для худшего случая до значения, близкого к VE (см. раздел ссылок).
(для разреженных графов
V5/2
) (см. раздел ссылок). Как обычно, эта оценка слишком осторожна. Было предложено и множество других вариантов проталкивания напора, и некоторые из них понижают границу времени для худшего случая до значения, близкого к VE (см. раздел ссылок).
В таблице 22.2 сведены значения производительности, показанные алгоритмами проталкивания напора, которые соответствуют приведенным в таблице 22.1 результатам алгоритмов с использованием расширяющих путей, для двух моделей сетей из раздела 22.2. Эти эксперименты для различных алгоритмов проталкивания напора показывают гораздо меньшие различия в производительности, чем в случае различных методов расширения путей.
Данная последовательность диаграмм показывает, как реализация метода проталкивания напора с использованием очереди FIFO находит максимальный поток в демонстрационной сети. Он работает поэтапно. Сначала он проталкивает максимально возможный поток из истока по исходящим из него ребрам (слева вверху). Затем он проталкивает поток из каждого такого узла и продолжает так, пока не будет достигнут баланс для всех узлов.
В этой таблице приведены значения производительности (количество вершин, где величина потока увеличивалась, и количество просмотренных узлов из списков смежности) для различных алгоритмов проталкивания напора на нашем примере евклидовой сети с соседними связями (со случайными значениями пропускных способностей и максимальным потоком 286), и с единичными пропускными способностями (максимальный поток равен 6). Различия в результатах этих методов для обоих видов сетей минимальны. Для случайных пропускных способностей количество проверяемых ребер примерно то же, что и для алгоритма расширения путей (см. таблицу 22.1). Для единичных пропускных способностей алгоритмы с использованием расширяющих путей просматривают в этих сетях значительно меньше ребер.
| Вершины | Ребра | |
|---|---|---|
| Случайные пропускные способности от 1 до 50 | ||
| Кратчайшие пути | 2450 | 57746 |
| Поиск в глубину | 2476 | 58258 |
| Случайный поиск | 2363 | 55470 |
| Единичные пропускные способности | ||
| Кратчайшие пути | 1192 | 28356 |
| Поиск в глубину | 1234 | 29040 |
| Случайный поиск | 1390 | 33018 |
Существует множество способов изучения реализаций алгоритмов проталкивания напора. Мы уже рассмотрели три основных варианта:
- Сравнение вершинного обобщенного алгоритма с реберным.
- Реализация обобщенной очереди.
- Первоначальное присваивание высот.
Можно рассмотреть несколько других возможностей и множество вариаций каждой из них, которые порождают множество различных алгоритмов (см., например, упражнения 22.56-22.60). Зависимость производительности алгоритмов от характеристик входной сети еще больше увеличивает количество возможностей.
Два рассмотренных нами обобщенных алгоритма (расширением путей и проталкиванием напора) входят в число важнейших алгоритмов, описанных в исследовательской литературе по алгоритмам вычисления максимальных потоков. Поиск более совершенных алгоритмов вычисления максимальных потоков все еще остается перспективной областью для дальнейших исследований. Исследователи разрабатывают и исследуют новые алгоритмы и реализации, надеясь получить более быстрые алгоритмы для практических проблем, а то и простой линейный алгоритм для задачи вычисления максимального потока. Но пока такого алгоритма нет, можно спокойно работать с рассмотренными нами алгоритмами и реализациями: многочисленные исследования показывают, что они вполне эффективны для широкого класса практических задач, требующих вычисления максимальных потоков.
Упражнения
22.49. Опишите работу алгоритма проталкивания напора в сети со сбалансированными пропускными способностями.
22.50. Воспользуйтесь концепциями, описанными в данном разделе (функции высоты, подходящие ребра и проталкивание потока через ребра), для описания алгоритмов вычисления максимального потока расширением путей.
22.51. Покажите в стиле рис. 22.28 потоки и остаточные сети после каждого этапа работы алгоритма проталкивания напора с очередью FIFO для отыскания максимального потока в транспортной сети с рис. 22.10.
22.52. Реализуйте функцию initheights() для программы 22.5 с помощью поиска в ширину от стока.
22.53. Выполните упражнение 22.51 для алгоритма проталкивания напора из вершины с максимальной высотой.
22.54. Измените программу 22.5, чтобы реализовать алгоритм проталкивания напора из вершины с максимальной высотой, реализовав обобщенную очередь в виде очереди с приоритетами. Проведите эмпирическое тестирование, чтобы добавить в таблицу 22.2 строку для этого варианта алгоритма.
22.55. Начертите графики зависимости количества активных вершин, а также количества вершин и ребер в остаточной сети по мере выполнения алгоритма проталкивания напора с очередью FIFO для конкретных примеров различных сетей (см. упражнения 22.7-22.12).
22.56. Реализуйте обобщенный реберный алгоритм проталкивания напора, который использует обобщенную очередь подходящих ребер. Эмпирически сравните его работу для различных сетей (см. упражнения 22.7-22.12) с базовыми методами, уделяя особое внимание наиболее быстрым реализациям обобщенных очередей.
22.57. Добавьте в программу 22.5 периодический пересчет высот вершин, равных кратчайшим путям в сток в остаточной сети.
22.58. Обдумайте идею равномерного распределения избыточного потока из вершин в исходящие ребра, а не заполнения одних до насыщения, оставляя другие пустыми.
22.59. Эмпирически определите оправданность вычисления кратчайших путей для первоначального задания функции высоты в программе 22.5, сравнив ее производительность для различных сетей (см. упражнения 22.7-22.12) с производительностью при первоначальном обнулении высот вершин.
22.60. Поэкспериментируйте с гибридными методами, содержащими различные сочетания описанных выше идей. Эмпирически сравните различные виды сетей (см. упражнения 22.7-22.12) с базовыми методами, уделяя особое внимание наиболее быстрым вариантам.
22.61. Добавьте в программу 22.5 явное отбрасывание повторяющихся вершин перед занесением в обобщенную очередь. Эмпирически определите для различных сетей (см. упражнения 22.7-22.12), как влияют эти изменения на реальное время выполнения.
22.62. Как повлияет разрешение заносить повторяющиеся вершины в обобщенную очередь на границу времени выполнения в худшем случае из леммы 22.13?
22.63. Измените реализацию программы 22.5, чтобы использовать явное представление остаточной сети.
о 22.64. Уточните границу O (V3) из леммы 12.13 для реализации из упражнения 22.63. Указание. Приведите отдельные границы для количества проталкиваний, которые соответствуют удалению ребер из остаточной сети, и для количества проталкиваний, в результате которых не появляются заполненные или пустые ребра.
22.65. Эмпирически определите для различных сетей (см. упражнения 22.7-22.12) влияние использования явных представлений остаточной сети (см. упражнение 22.63) на реальные значения времени выполнения.
22.66. Докажите, что в реберном обобщенном алгоритме проталкивания напора количество проталкиваний, которые соответствуют удалению ребра из остаточной сети, меньше 2VE . Считайте, что в реализации используется явное представление остаточной сети.
22.67. Докажите, что в реберном обобщенном алгоритме проталкивания напора количество проталкиваний, которые не соответствуют удалению ребра из остаточной сети, меньше 4V2( V+E). Указание. Используйте сумму высот активных вершин в качестве функции потенциала.
22.68. Эмпирически определите фактическое количество проверяемых ребер и отношение времени прогона к V для различных версий алгоритма проталкивания напора и для различных сетей (см. упражнения 22.7-22.12). Рассмотрите различные алгоритмы, описанные в тексте и в предыдущих упражнениях, уделяя особое внимание тем, которые лучше работают на больших разреженных сетях. Сравните ваши результаты с результатами из упражнения 22.34.
22.69. Напишите клиентскую программу для графической анимации динамики алгоритма проталкивания напора. Эта программа должна создавать изображения, подобные рис. 22.30 и другим рисункам из этого раздела (см. упражнение 22.48). Протестируйте полученную реализацию на евклидовых сетях из упражнений 22.7-22.12.