|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Принципы анализа алгоритмов
Примеры анализа алгоритмов
Вооружившись инструментами, о которых было рассказано в трех предыдущих разделах, мы рассмотрим анализ последовательного поиска и бинарного поиска - двух основных алгоритмов для определения того, входит ли некоторая последовательность объектов в заданное множество объектов. Наша цель - показать, как можно сравнивать алгоритмы, а не подробно описать сами алгоритмы. Для простоты предположим, что все рассматриваемые объекты являются целыми числами. Более общие приложения будут подробно рассмотрены в лекциях 12 - 16 . Простые версии алгоритмов, которые мы сейчас рассмотрим, не только демонстрируют многие аспекты задачи их разработки и анализа, но и имеют практическую ценность.
Например, представим себе компанию, обрабатывающую кредитные карточки и имеющую  рискованных или украденных кредитных карточек. При этом компании необходимо проверять, нет ли среди
рискованных или украденных кредитных карточек. При этом компании необходимо проверять, нет ли среди  транзакций какого-либо из этих
транзакций какого-либо из этих  плохих номеров. Для большей конкретности будем считать
плохих номеров. Для большей конкретности будем считать  большим (скажем, порядка
большим (скажем, порядка  -
-  ), а
), а  - огромным (порядка
- огромным (порядка  -
-  ). Цель анализа заключается в приблизительной оценке времен выполнения алгоритмов, когда параметры принимают значения из указанного диапазона.
). Цель анализа заключается в приблизительной оценке времен выполнения алгоритмов, когда параметры принимают значения из указанного диапазона.
В программе 2.1 реализовано прямое решение задачи поиска. Для совместимости с другими вариантами кода для этой задачи, которые мы исследуем в части 4, она оформлена как функция С++, обрабатывающая массив (см. "Элементарные структуры данных" ). Однако необязательно вдаваться в детали программы для понимания алгоритма: мы сохраняем все объекты в массиве, затем для каждой транзакции мы последовательно просматриваем массив от начала до конца, проверяя, содержится ли в нем искомый номер.
Для анализа алгоритма прежде всего отметим, что время выполнения зависит от того, находится ли требуемый объект в массиве. Если поиск не является успешным, мы можем определить это, только проверив все  объектов, но успешный поиск может завершиться на первом, втором или любом другом объекте.
объектов, но успешный поиск может завершиться на первом, втором или любом другом объекте.
Поэтому время выполнения зависит от данных. Если бы все поиски выполнялись для чисел, которые находятся в первой позиции, то алгоритм был бы быстрым; если бы они выполнялись для чисел, находящихся в последней позиции, тогда алгоритм был бы медленным. В разделе 2.7 мы обсудим разницу между возможностью гарантировать производительность и предсказать производительность. В данном случае лучшее, что мы можем гарантировать - это что будет просмотрено не более  чисел.
чисел.
Однако чтобы сделать прогноз, необходимо какое-то предположение о данных. В данном случае предположим, что все числа выбраны случайным образом.
Программа 2.1. Последовательный поиск
Данная функция проверяет, находится ли число v среди элементов массива a[l] , a[l+1], ..., a[r], путем последовательного сравнения с каждым элементом, начиная с начала. Если по достижении последнего элемента нужное значение не найдено, функция возвращает значение -1. Иначе она возвращает индекс элемента массива, содержащего искомое число.
int search(int a[], int v, int l, int r) {
for (int i = l; i <= r; i++)
if (v == a[i]) return i;
return -1;
}
Из этого предположения следует, например, что предметом поиска с одинаковой вероятностью может оказаться каждое число в таблице. После некоторых размышлений мы приходим к выводу, что именно это свойство поиска является наиболее важным, потому что среди случайно выбранных чисел вряд ли найдется нужное нам (см. упражнение 2.48). В некоторых приложениях количество транзакций с успешным поиском может быть высоким, а в других - низким. Чтобы не запутывать модель свойствами приложения, мы разобьем задачу на два случая (успешный и неудачный поиск) и проанализируем их независимо. Данный пример иллюстрирует, что важным моментом эффективного анализа является разработка разумной модели приложения. Наши аналитические результаты будут зависеть от доли успешных поисков; более того, они обеспечат нас информацией, необходимой для выбора различных алгоритмов для разных приложений на основании этого параметра.
Лемма 2.1. Последовательный поиск проверяет  чисел при каждом неудачном поиске и в среднем порядка N/ 2 чисел при каждом успешном поиске.
чисел при каждом неудачном поиске и в среднем порядка N/ 2 чисел при каждом успешном поиске.
Если объектом поиска с равной вероятностью может быть любое число в таблице, то средняя стоимость поиска равна (1 + 2 + ... + N) / N = (N + 1)/ 2. 
Из леммы 2.1 следует, что время выполнения программы 2.1 пропорционально  , если средняя стоимость сравнения двух чисел постоянна. Значит, к примеру, можно ожидать, что если удвоить количество объектов, то и время, необходимое для поиска, также удвоится.
, если средняя стоимость сравнения двух чисел постоянна. Значит, к примеру, можно ожидать, что если удвоить количество объектов, то и время, необходимое для поиска, также удвоится.
Последовательный поиск в случае неудачи можно ускорить, если упорядочить числа в таблице. Сортировка чисел в таблице является предметом рассмотрения глав 6-11. Несколько алгоритмов, которые мы рассмотрим, выполняют эту задачу за время, пропорциональное 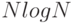 , которое незначительно по сравнению со стоимостью поиска при очень больших M. В упорядоченной таблице можно прервать поиск сразу по достижении числа, большего, чем искомое. Такое изменение уменьшает стоимость последовательного поиска до N/ 2 чисел, которые необходимо в среднем проверить при неудачном поиске, что совпадает с затратами для успешного поиска.
, которое незначительно по сравнению со стоимостью поиска при очень больших M. В упорядоченной таблице можно прервать поиск сразу по достижении числа, большего, чем искомое. Такое изменение уменьшает стоимость последовательного поиска до N/ 2 чисел, которые необходимо в среднем проверить при неудачном поиске, что совпадает с затратами для успешного поиска.
Лемма 2.2. Алгоритм последовательного поиска в упорядоченной таблице проверяет  чисел для каждого поиска в худшем случае и порядка
чисел для каждого поиска в худшем случае и порядка 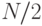 чисел в среднем.
чисел в среднем.
Здесь все еще необходимо определить модель неудачного поиска. Этот результат следует из предположения, что поиск может с равной вероятностью закончиться на любом из 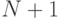 интервалов, задаваемых
интервалов, задаваемых  числами таблицы, а это непосредственно приводит к выражению
числами таблицы, а это непосредственно приводит к выражению  .
.
Стоимость неудачного поиска, который заканчивается до или после N-ой записи в таблице, такая же:  .
. 
Другой способ выразить результат леммы 2.2 - это сказать, что время выполнения последовательного поиска пропорционально 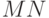 для
для  транзакций и в среднем, и в худшем случае. Если удвоить или количество транзакций, или количество объектов в таблице, то время выполнения удвоится; если мы удвоим обе величины одновременно, то время выполнения увеличится в 4 раза. Этот результат говорит о том, что данный метод не годится для очень больших таблиц. Если для проверки одного числа требуется c микросекунд, а
транзакций и в среднем, и в худшем случае. Если удвоить или количество транзакций, или количество объектов в таблице, то время выполнения удвоится; если мы удвоим обе величины одновременно, то время выполнения увеличится в 4 раза. Этот результат говорит о том, что данный метод не годится для очень больших таблиц. Если для проверки одного числа требуется c микросекунд, а  и
и  , то время выполнения для всех транзакций будет равно, по крайней мере,
, то время выполнения для всех транзакций будет равно, по крайней мере,  секунд, или, согласно
рис.
2.1, около 16c лет, что недопустимо.
секунд, или, согласно
рис.
2.1, около 16c лет, что недопустимо.
Программа 2.2. Бинарный поиск
Эта программа делает то же самое, что и программа 2.1, но гораздо эффективнее.
int search(int a[], int v, int l, int r) {
while (r >= l) {
int m = (l+r)/2;
if ( v == a[ m] ) return m;
if (v < a[m]) r = m-1; else l = m+1;
}
return -1;
}
Программа 2.2 представляет собой классическое решение задачи поиска методом, гораздо более эффективным, чем последовательный поиск. Он основан на идее, что если числа в таблице упорядочены, то после сравнения искомого значения с числом из середины таблицы мы можем отбросить половину из них. Если они равны, значит, поиск завершен успешно, если искомое число меньше, то мы применим этот же метод к левой части таблицы, а если больше - то к правой. На рис. 2.7 представлен пример выполнения этого метода на множестве чисел.
Лемма 2.3. Бинарный поиск проверяет не более  чисел.
чисел.
Доказательство данной леммы иллюстрирует применение рекуррентных соотношений при анализе алгоритмов. Пусть 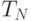 - это количество сравнений, необходимое бинарному поиску в худшем случае. Тогда из сведения поиска в таблице размером
- это количество сравнений, необходимое бинарному поиску в худшем случае. Тогда из сведения поиска в таблице размером  к поиску в два раза меньшей таблице непосредственно следует, что
к поиску в два раза меньшей таблице непосредственно следует, что

При поиске в таблице размером  мы проверяем число посредине, затем производим поиск в таблице размером не более
мы проверяем число посредине, затем производим поиск в таблице размером не более 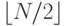 . Реальная стоимость может быть меньше этого значения, так как сравнение может закончиться успешно или таблица будет иметь размер
. Реальная стоимость может быть меньше этого значения, так как сравнение может закончиться успешно или таблица будет иметь размер 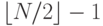 (если
(если  четно). Так же, как это было сделано в решении формулы 2.2, легко доказать, что
четно). Так же, как это было сделано в решении формулы 2.2, легко доказать, что 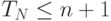 при
при  , а затем получить общий результат с помощью индукции.
, а затем получить общий результат с помощью индукции. 
Чтобы проверить, содержится ли число 5025 в таблице, приведенной в левой колонке, мы сначала сравниваем его с 6504, из чего следует, что дальше необходимо рассматривать первую половину массива. Затем производится сравнение с числом 4548 (середина первой половины), что приводит нас ко второй половине первой половины. Мы продолжаем этот процесс, постоянно работая с подмассивом, в котором может содержаться искомое число, если оно есть в таблице. В заключение мы получаем подмассив с одним элементом, не равным 5025, из чего следует, что 5025 в таблице не содержится.
Лемма 2.3 позволяет решить очень большую задачу поиска в 1 миллионе чисел при помощи 20 сравнений на транзакцию, то есть быстрее, чем требуется для чтения или записи числа на большинстве современных компьютеров. Задача поиска настолько важна, что было разработано несколько еще более быстрых методов, чем приведенный здесь (см. лекции 12 - 16).
В формулировках лемм 2.1 и 2.2 используются операции, наиболее часто выполняемые над данными. Как отмечено в комментарии, следующем за леммой 2.1, мы предполагаем, что каждая операция должна занимать постоянное время, тогда можно заключить, что время выполнения бинарного поиска пропорционально lgN, в отличие от  для последовательного поиска. При удвоении
для последовательного поиска. При удвоении  время бинарного поиска несколько увеличивается, но не удваивается, как это имеет место для последовательного поиска. С ростом
время бинарного поиска несколько увеличивается, но не удваивается, как это имеет место для последовательного поиска. С ростом  разница между двумя методами становится огромной.
разница между двумя методами становится огромной.
Аналитическое доказательство лемм 2.1 и 2.2 можно проверить, написав программу и протестировав алгоритм. Например, в
таблица
2.4 показаны времена выполнения бинарного и последовательного поиска для  поисков в таблице размером
поисков в таблице размером  (включая в случае бинарного поиска и затраты на сортировку таблицы) при различных значениях
(включая в случае бинарного поиска и затраты на сортировку таблицы) при различных значениях  и
и  . Здесь мы не будем рассматривать реализацию программы и проводить эксперименты, поскольку похожие задачи будут подробно рассмотрены в
"Элементарные методы сортировки"
и 11. Кроме того, использование библиотечных и внешних функций и другие детали создания программ из отдельных компонентов, включая и функцию sort, объясняются в
"Элементарные структуры данных"
. Так что пока мы просто подчеркнем, что проведение эмпирического тестирования - это неотъемлемая часть оценки эффективности алгоритма.
. Здесь мы не будем рассматривать реализацию программы и проводить эксперименты, поскольку похожие задачи будут подробно рассмотрены в
"Элементарные методы сортировки"
и 11. Кроме того, использование библиотечных и внешних функций и другие детали создания программ из отдельных компонентов, включая и функцию sort, объясняются в
"Элементарные структуры данных"
. Так что пока мы просто подчеркнем, что проведение эмпирического тестирования - это неотъемлемая часть оценки эффективности алгоритма.
Таблица 2.4 подтверждает наше наблюдение, что функциональный рост времени выполнения позволяет предсказать производительность в случае больших значений параметров на основе эмпирического изучения работы алгоритма при малых значениях. Сочетание математического анализа и эмпирического изучения убедительно показывает, что предпочтительным алгоритмом является бинарный поиск.
Данный пример является прототипом нашего общего подхода к сравнению алгоритмов. Математический анализ используется для оценки частоты выполнения абстрактных операций в алгоритме, а затем на основе этих результатов выводится функциональная форма времени выполнения, которая позволяет проверить и расширить эмпирические данные.
При необходимости все более точных алгоритмических решений вычислительных задач и сложного математического анализа характеристик производительности мы будем обращаться за математическими результатами к специальной литературе, чтобы основное внимание в книге уделять самим алгоритмам. Здесь нет возможности производить тщательное математическое и эмпирическое изучение всех алгоритмов, а нашей главной задачей является определение наиболее существенных характеристик производительности. При этом, в принципе, всегда можно разработать научную основу, необходимую для осознанного выбора алгоритмов для важных приложений.
Упражнения
-
2.47. Найдите среднее число сравнений, используемых программой 2.1, если
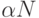 поисков оказались успешными,
поисков оказались успешными,  .
.
-
2.48. Оцените вероятность того, что хотя бы одно из
 случайных десятизначных чисел будет содержаться в наборе из
случайных десятизначных чисел будет содержаться в наборе из  чисел, при
чисел, при 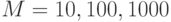 и
и 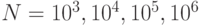 .
.
-
2.49. Напишите вызывающую программу, которая генерирует
 целых чисел и помещает их в массив, затем подсчитывает количество
целых чисел и помещает их в массив, затем подсчитывает количество  случайных целых чисел, которые совпадают с одним из чисел массива, используя последовательный поиск. Запустите программу при
случайных целых чисел, которые совпадают с одним из чисел массива, используя последовательный поиск. Запустите программу при 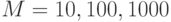 и
и 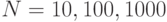 .
.
- 2.50. Сформулируйте и докажите лемму, аналогичную лемме 2.3 для бинарного поиска.
Приведенные ниже относительные времена выполнения подтверждают наши аналитические результаты: в случае  поисков в таблице из
поисков в таблице из  объектов время последовательного поиска пропорционально MN, а время бинарного поиска -
объектов время последовательного поиска пропорционально MN, а время бинарного поиска - 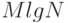 . При удвоении
. При удвоении  время последовательного поиска также удваивается, а время бинарного поиска ненамного увеличивается. Последовательный поиск неприменим для очень больших
время последовательного поиска также удваивается, а время бинарного поиска ненамного увеличивается. Последовательный поиск неприменим для очень больших  и
и  , а бинарный поиск выполняется достаточно быстро даже для огромных таблиц.
, а бинарный поиск выполняется достаточно быстро даже для огромных таблиц.
| N |
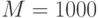
|
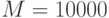
|

|
|||
|---|---|---|---|---|---|---|
| S | B | S | B | S | B | |
| 125 | 1 | 1 | 13 | 2 | 130 | 20 |
| 250 | 3 | 0 | 25 | 2 | 251 | 22 |
| 500 | 5 | 0 | 49 | 3 | 492 | 23 |
| 1250 | 13 | 0 | 128 | 3 | 1276 | 25 |
| 2500 | 26 | 1 | 267 | 3 | 28 | |
| 5000 | 53 | 0 | 533 | 3 | 30 | |
| 12500 | 134 | 1 | 1337 | 3 | 33 | |
| 25000 | 268 | 1 | 3 | 35 | ||
| 50000 | 537 | 0 | 4 | 39 | ||
| 100000 | 1269 | 1 | 5 | 47 | ||
Обозначения:
S последовательный поиск (программа 2.1)
B бинарный поиск (программа 2.2)

