|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Принципы анализа алгоритмов
В наших алгоритмах и их анализе часто бывают нужны дискретные единицы, поэтому часто требуются специальные функции, преобразующие действительные числа в целые:
 : наибольшее целое, меньшее или равное x
: наибольшее целое, меньшее или равное x
 : наименьшее целое, большее или равное х.
: наименьшее целое, большее или равное х.
Например, 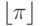 и
и 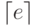 оба равны 3, а
оба равны 3, а  - это количество битов, необходимое для двоичного представления числа
- это количество битов, необходимое для двоичного представления числа  . Другое важное применение этих функций возникает в том случае, когда необходимо поделить множество
. Другое важное применение этих функций возникает в том случае, когда необходимо поделить множество  объектов пополам. Этого нельзя сделать точно, если
объектов пополам. Этого нельзя сделать точно, если  является нечетным, поэтому для точности мы можем создать одно подмножество, содержащее
является нечетным, поэтому для точности мы можем создать одно подмножество, содержащее 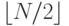 объектов, а второе -
объектов, а второе - 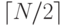 объектов. Если
объектов. Если  четно, тогда размеры обоих поднаборов равны (
четно, тогда размеры обоих поднаборов равны ( 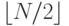 =
= 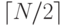 ); если же
); если же  нечетно, то их размер отличается на единицу (
нечетно, то их размер отличается на единицу ( =
= 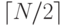 ). В С++ можно напрямую подсчитать значения этих функций при выполнении операций над целыми числами (например, если $N\geq0$N, тогда
). В С++ можно напрямую подсчитать значения этих функций при выполнении операций над целыми числами (например, если $N\geq0$N, тогда 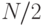 равно
равно 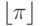 а
а 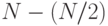 равно
равно  ), а при операциях над числами с плавающей точкой можно воспользоваться функциями floor и ceil из заголовочного файла math.h.
), а при операциях над числами с плавающей точкой можно воспользоваться функциями floor и ceil из заголовочного файла math.h.
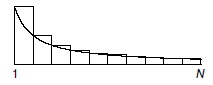
При анализе алгоритмов часто возникает дискретизированная версия функции натурального логарифма, называемая гармоническими числами. N-е гармоническое число определяется выражением
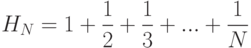
Натуральный логарифм 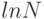 - это значение площади под кривой
- это значение площади под кривой 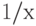 между 1 и
между 1 и  ; гармоническое число H_N - это площадь под ступенчатой функцией, которую можно определить, вычисляя значения функции
; гармоническое число H_N - это площадь под ступенчатой функцией, которую можно определить, вычисляя значения функции 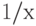 для целых чисел от 1 до
для целых чисел от 1 до  . Эта зависимость показана на
рис.
2.2.
. Эта зависимость показана на
рис.
2.2.
Гармонические числа представляют собой приближенные значения площади под кривой 1/х. Постоянная y учитывает разницу между H_N и 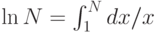
Формула
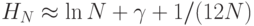 где
где 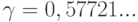 (эта константа называется постоянной Эйлера), дает отличное приближение для H_N. В отличие от
(эта константа называется постоянной Эйлера), дает отличное приближение для H_N. В отличие от 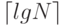 и
и 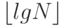 для вычисления H_N лучше воспользоваться библиотечной функцией log, а не подсчитывать его непосредственно из определения.
для вычисления H_N лучше воспользоваться библиотечной функцией log, а не подсчитывать его непосредственно из определения.
Последовательность чисел
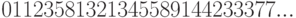 определяемая формулой
определяемая формулой 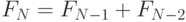 где
где
 а
а 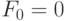 и
и  известна как числа Фибоначчи и имеет множество интересных свойств. Например, отношение двух последовательных чисел приближенно равно золотому сечению (golden ratio)
известна как числа Фибоначчи и имеет множество интересных свойств. Например, отношение двух последовательных чисел приближенно равно золотому сечению (golden ratio) 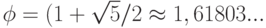 Более подробный анализ показывает, что
Более подробный анализ показывает, что 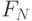 равно значению выражения
равно значению выражения 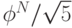 округленному до ближайшего целого числа.
округленному до ближайшего целого числа.
При анализе алгоритмов часто встречается также функция факториал 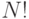 . Как и экспоненциальная функция, факториал возникает при лобовом решении задач и растет слишком быстро, чтобы такие решения представляли практический интерес. Он также возникает при анализе алгоритмов, поскольку представляет собой количество способов упорядочения
. Как и экспоненциальная функция, факториал возникает при лобовом решении задач и растет слишком быстро, чтобы такие решения представляли практический интерес. Он также возникает при анализе алгоритмов, поскольку представляет собой количество способов упорядочения  объектов.
объектов.
Для аппроксимации 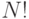 используется формула Стирлинга:
используется формула Стирлинга:
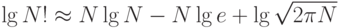 .
.
Например, из формулы Стирлинга следует, что количество битов в представлении числа 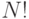 примерно равно
примерно равно 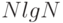 .
.
Большинство рассматриваемых в этой книге формул выражается через несколько функций, рассмотренных в этой главе. Однако при анализе алгоритмов может встретиться множество других специальных функций.
Например, классическое биномиальное распределение и распределение Пуассона играют важную роль при разработке и анализе некоторых фундаментальных поисковых алгоритмов, которые будут рассмотрены в "Хеширование" и "Поразрядный поиск" . Функции, не приведенные здесь, обсуждаются по мере их появления.
Упражнения
 2.5. Для каких значений
2.5. Для каких значений  справедливо
справедливо 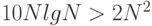 ?
?
 2.6. Для каких значений
2.6. Для каких значений  выражение
выражение  имеет значение в пределах от
имеет значение в пределах от 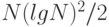 до
до 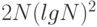 ?
?
-
2.7. Для каких значений
 справедливо
справедливо 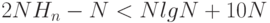 ?
?
-
2.8. Для какого наименьшего значения
 справедливо
справедливо  ?
?
-
2.9. Докажите, что
 + 1 - это количество битов, необходимое для представления числа
+ 1 - это количество битов, необходимое для представления числа  в двоичной форме.
в двоичной форме.
-
2.10. Добавьте в
таблица
2.2 столбцы для
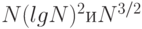 .
.
-
2.11. Добавьте в
таблица
2.2 строки для
 и
и  инструкций в секунду.
инструкций в секунду.
-
2.12. Напишите на С++ функцию, которая подсчитывает
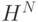 , используя функцию
, используя функцию  из стандартной математической библиотеки.
из стандартной математической библиотеки.
-
2.13. Напишите эффективную функцию на С++, подсчитывающую
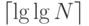 Не используйте библиотечную функцию.
Не используйте библиотечную функцию.
- 2.14. Сколько цифр в десятичном представлении числа 1 миллион факториал?
-
2.15. Сколько битов в двоичном представлении числа
 ?
?
-
2.16. Сколько битов в двоичном представлении
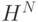 ?
?
-
2.17. Приведите простое выражение для
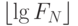 .
.
-
2.18. Приведите наименьшие значения
 , для которых
, для которых 
-
2.19. Приведите наибольшее значение
 , для которого можно решить задачу, требующую выполнения f(N) инструкций, на машине с быстродействием
, для которого можно решить задачу, требующую выполнения f(N) инструкций, на машине с быстродействием  операций в секунду для следующих функций
операций в секунду для следующих функций 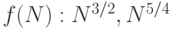 ,
, 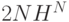 ,
, 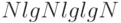 и
и 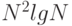 .
.