Диаграммы
Теория полугрупп
Наш второй пример — теория полугрупп. Ее сигнатура состоит из
равенства и единственного двуместного функционального символа,
называемого умножением; результат умножения 
и 
мы
будем обозначать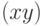 
.
Теория состоит из аксиом равенства (включая корректность
умножения: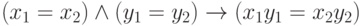 
; мы опускаем внешние кванторы всеобщности) и
аксиомы ассоциативности
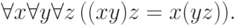
Нормальные модели этой теории называются полугруппами.
Теорема 69. Множество теорем теории полугрупп (множество замкнутых формул указанной сигнатуры, истинных во всех полугруппах) неразрешимо.
Нам понадобится конкретный способ задания полугрупп с помощью образующих и соотношений. Пусть фиксировано некоторое конечное множество, называемое алфавитом. Элементы его называют буквами, а конечные последовательности букв — словами (данного алфавита). На словах определена операция соединения (приписывания), относительно которой они образуют полугруппу, которая называется свободной полугруппой. Эта полугруппа имеет нейтральный элемент — пустое слово, приписывание которого к любому слову не меняет последнего.
Пусть фиксирован алфавит 
, а также конечное число
пар слов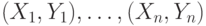 
этого алфавита. Два слова алфавита назовем
эквивалентными, если одно можно превратить в другое, многократно
делая замены подслов вида 
. Легко
проверить, что получается отношение эквивалентности и что
операция приписывания корректно определена на классах
эквивалентности и ассоциативна. Получается полугруппа. Ее
называют полугруппой с образующими из и
соотношениями 
.
141. Сколько элементов в полугруппе с образующими 
и 
и
соотношениями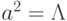 
, 
, 
(через 
мы обозначаем пустое слово)? (Ответ: 
; это
группа 
.)
Известно, что существуют такие образующие и соотношения, при которых проблема равенства слов (выяснить, принадлежат ли два данных слова одному классу эквивалентности) является алгоритмически неразрешимой (подробнее см. в [5]). Мы сейчас покажем, что этот вопрос можно свести к вопросу о выводимости некоторой формулы в теории полугрупп, так что если бы она была разрешимой, то получилось бы противоречие.
Построение такой формулы происходит весьма естественным образом;
мы поясним его на примере. Пусть мы хотим узнать, будут ли
слова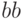 
и равны в полугруппе с
образующими и и
соотношениями 
и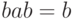 
. (Другими словами, мы
хотим узнать, можно ли из слова 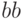получить слово с
помощью замен подслов 
и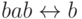 
.) Как сформулировать этот вопрос в терминах формул?
Напишем такую формулу:
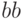и эквивалентны в указанной
полугруппе, заданной образующими и соотношениями. В самом деле, если одно
слово можно получить из другого заменами, то эти замены
(в предположени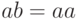и 
и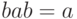 
) ничего не меняют и 
, так что написанная формула истинна во всех
полугруппах.Напротив, если слово не получается из
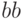заменой, то существует полугруппа, в которой эта формула не истинна: надо взять как раз
полугруппу с образующими и и соотношениями и 
, значением переменной считать класс слова , а значением переменной считать класс слова . Тогда
значением терма 
будет класс слова , равный
классу слова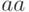 
по построению полугруппы. Аналогичным образом при такой
оценке будет истинно и равенство . А равенство 
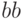не будет истинно, так как значение терма есть класс
слова 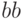, значение терма есть класс
слова , а эти классы различны по предположению.
Таким образом, любой алгоритм, проверяющий истинность формул в классе всех полугрупп, можно было бы использовать для проверки равенства двух слов в полугруппе, заданной образующими и соотношениями. А среди таких полугрупп есть неразрешимые.
Теория групп (в которой, помимо ассоциативности, есть еще аксиомы существования единицы и обратного), также неразрешима, но доказательство этого сложнее, чем для полугрупп. Это и не удивительно, поскольку из неразрешимости теории групп формально выводится неразрешимость теории полугрупп, как показывает следующая задача.
142. Пусть теория 
разрешима, а теория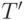 
той же
сигнатуры получается из добавлением конечного числа аксиом. Тогда
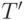теория разрешима. (Указание: дополнительные аксиомы
соединяем конъюнкциями и помещаем в посылку импликации.)
Добавление аксиом может сделать неразрешимую теорию разрешимой. Например, как мы уже упоминали, это происходит с теорией групп при добавлении аксиомы коммутативности.