Диаграммы
Теорема 73. Теория является 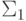 -аксиоматизируемой тогда и только
тогда, когда она устойчива относительно перехода к расширениям.
-аксиоматизируемой тогда и только
тогда, когда она устойчива относительно перехода к расширениям.
151. Проведите подробно соответствующее рассуждение (дав необходимые определения).
152. Докажите, что если формула устойчива относительно перехода к
расширениям, то она выводимо эквивалентна 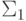 -формуле
той же сигнатуры.
-формуле
той же сигнатуры.
Теоретико-модельные критерии существуют и для других классов
формул, в частности 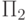 -формул (то есть формул типа
-формул (то есть формул типа 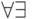 ). Такие формулы не устойчивы ни относительно
расширений, ни относительно подструктур. Рассмотрим, например,
утверждение об отсутствии наибольшего элемента в упорядоченном
множестве. Оно записывается в виде
). Такие формулы не устойчивы ни относительно
расширений, ни относительно подструктур. Рассмотрим, например,
утверждение об отсутствии наибольшего элемента в упорядоченном
множестве. Оно записывается в виде 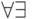 -формулы.
Истинность его в некотором множестве вовсе не влечет его
истинность в подмножествах и в расширениях. Тем не менее кое-
что об этом утверждении сказать можно: если ни одно из множеств
возрастающей цепи
-формулы.
Истинность его в некотором множестве вовсе не влечет его
истинность в подмножествах и в расширениях. Тем не менее кое-
что об этом утверждении сказать можно: если ни одно из множеств
возрастающей цепи 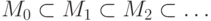 не имеет наибольшего элемента, то и объединение
не имеет наибольшего элемента, то и объединение 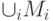 не
имеет наибольшего элемента (проверьте). Именно это свойство, как
мы вскоре увидим, характеризует
не
имеет наибольшего элемента (проверьте). Именно это свойство, как
мы вскоре увидим, характеризует 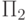 -формулы.
-формулы.
Пусть дана последовательность
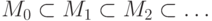
 , причем
, причем  является
подструктурой
является
подструктурой 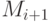 (предикаты и функции согласованы). Тогда
объединение этой возрастающей цепи интерпретаций также является
(нормальной) интерпретацией сигнатуры
(предикаты и функции согласованы). Тогда
объединение этой возрастающей цепи интерпретаций также является
(нормальной) интерпретацией сигнатуры  . (Подобная
конструкция используется в теории полей, когда строится
алгебраическое замыкание счетного поля: мы расширяем поле,
добавляя по очереди корни различных многочленов, а потом берем
объединение этих полей.)
. (Подобная
конструкция используется в теории полей, когда строится
алгебраическое замыкание счетного поля: мы расширяем поле,
добавляя по очереди корни различных многочленов, а потом берем
объединение этих полей.)Заметим, что любая 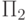 -формула устойчива относительно
объединения цепей: если она истинна во всех
-формула устойчива относительно
объединения цепей: если она истинна во всех  , то она
истинна и в их объединении. В самом деле, пусть формула
, то она
истинна и в их объединении. В самом деле, пусть формула 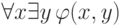 с бескванторной частью
с бескванторной частью 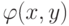 истинна во всех
истинна во всех  . Тогда она истинна
и в их объединении. В самом деле, любое
. Тогда она истинна
и в их объединении. В самом деле, любое  из объединения принадлежит
какому-то
из объединения принадлежит
какому-то  , и в том же самом
, и в том же самом  можно найти
подходящее
можно найти
подходящее  . (Если переменных несколько, рассуждение
аналогично.)
. (Если переменных несколько, рассуждение
аналогично.)
Поэтому и любая теория, имеющая 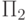 -аксиоматизацию,
устойчива относительно объединения. Обратное утверждение также
верно:
-аксиоматизацию,
устойчива относительно объединения. Обратное утверждение также
верно:
Теорема 74 (Чэна-Лося-Сушко). Теория является 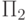 -аксиоматизируемой тогда и только
тогда, когда она устойчива относительно объединения возрастающих
цепей (объединение любой цепи ее моделей также является ее моделью).
-аксиоматизируемой тогда и только
тогда, когда она устойчива относительно объединения возрастающих
цепей (объединение любой цепи ее моделей также является ее моделью).
Доказательство этой теоремы использует понятие элементарного
расширения. Напомним, что  называется элементарным
расширением
называется элементарным
расширением  , если
, если 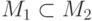 и в
и в  истинны те же формулы с константами из
истинны те же формулы с константами из  , что и в
, что и в  .
(Обозначение:
.
(Обозначение:  .)
.)
153. Покажите, что если  , то
, то 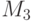 есть элементарное расширение
есть элементарное расширение  .
.
Лемма Тарского. Объединение цепи элементарных расширений  является элементарным расширением
каждой из интерпретаций цепи.
является элементарным расширением
каждой из интерпретаций цепи.
Доказательство леммы. Пусть параметрам формулы  приданы
значения в каком-либо из
приданы
значения в каком-либо из  . Нам надо доказать, что
полученная формула одновременно истинна или ложна в
. Нам надо доказать, что
полученная формула одновременно истинна или ложна в  и в
объединении цепи, которое мы обозначим через
и в
объединении цепи, которое мы обозначим через  . (Условие
леммы гарантирует, что формула
. (Условие
леммы гарантирует, что формула  с указанными значениями
параметров одновременно истинна или ложна во всех интерпретациях цепи, начиная с
с указанными значениями
параметров одновременно истинна или ложна во всех интерпретациях цепи, начиная с  .)
.)
Это утверждение доказывается индукцией по построению
формулы  . Для атомарных формул оно очевидно; для
логических операций индукция также проходит автоматически.
Единственный содержательный случай — это кванторы. Пусть формула
. Для атомарных формул оно очевидно; для
логических операций индукция также проходит автоматически.
Единственный содержательный случай — это кванторы. Пусть формула  начинается с квантора
начинается с квантора 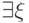 . Если
подходящее значение
. Если
подходящее значение  найдется уже в
найдется уже в  , то оно годится и
для
, то оно годится и
для  (пользуемся предположением индукции). В обратную сторону: если
подходящее
(пользуемся предположением индукции). В обратную сторону: если
подходящее  найдется в
найдется в  , то оно принадлежит
, то оно принадлежит 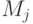 при достаточно большом
при достаточно большом  , поэтому формула истинна в
, поэтому формула истинна в 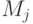 (предположение индукции). Остается вспомнить, что
(предположение индукции). Остается вспомнить, что 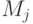 элементарно эквивалентно
элементарно эквивалентно  .
.
Как всегда, квантор всеобщности можно выразить с помощью квантора сушествования (или провести двойственное рассуждение). Лемма Тарского доказана.
Теперь докажем теорему Чэна-Лося-Сушко. Предположим, что
теория  устойчива относительно объединения цепей. Обозначим
через
устойчива относительно объединения цепей. Обозначим
через 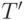 множество всех
множество всех 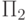 -теорем
-теорем  . Нам надо доказать, что любая модель
. Нам надо доказать, что любая модель 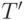 является моделью
является моделью  .
.
Для этого, начав с любой модели 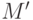 теории
теории 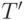 , мы
построим цепь интерпретаций
, мы
построим цепь интерпретаций
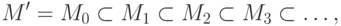
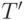 (интерпретации
(интерпретации 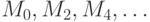 ), которые являются элементарными
расширениями друг друга, и модели теории
), которые являются элементарными
расширениями друг друга, и модели теории  (интерпретации
(интерпретации  ; они, впрочем, также будут моделями
теории
; они, впрочем, также будут моделями
теории  ).
).Объединение всех  будет моделью теории
будет моделью теории  , так
как эта теория устойчива относительно расширений. С другой стороны, по
лемме Тарского это объединение элементарно эквивалентно
интерпретациям
, так
как эта теория устойчива относительно расширений. С другой стороны, по
лемме Тарского это объединение элементарно эквивалентно
интерпретациям 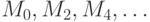 Поэтому все они, включая
исходную модель
Поэтому все они, включая
исходную модель  , будут моделями теории
, будут моделями теории  ,
что и требовалось доказать.
,
что и требовалось доказать.
Осталось построить требуемую цепь. Интерпретация  уже
есть. Будем строить цепь по шагам, продолжая ее на каждом шаге
на два звена вперед. Возможность этого обеспечивает такая лемма:
уже
есть. Будем строить цепь по шагам, продолжая ее на каждом шаге
на два звена вперед. Возможность этого обеспечивает такая лемма:
