Индуктивные определения и степени
Теорема 42.
Всякий ординал, меньший 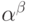 , представляется в
виде
, представляется в
виде
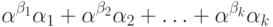
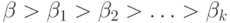 ,
а
,
а 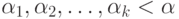 .
Такое представление однозначно и любая сумма указанного вида
является ординалом, меньшим
.
Такое представление однозначно и любая сумма указанного вида
является ординалом, меньшим 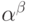 .
.Доказательство. Возможность такого представления мы уже доказали. Последнее
утверждение следует из того, что любая сумма такого вида
является начальным отрезком в множестве ![[B\to A]](/sites/default/files/tex_cache/dbea59e56a8b322788914be99997bd18.png) (где
(где  и
и  упорядочены по типам
упорядочены по типам  и
и  ) и разным
суммам соответствуют разные начальные отрезки.
) и разным
суммам соответствуют разные начальные отрезки.
Это утверждение обобщает описанную нами ранее
" позиционную систему обозначений с основанием  " для ординалов, меньших
" для ординалов, меньших 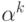 ; теперь вместо
; теперь вместо  можно использовать любой
ординал.
можно использовать любой
ординал.
Можно было бы сразу сказать, что элементами множества ![[B\to A]](/sites/default/files/tex_cache/dbea59e56a8b322788914be99997bd18.png) являются формальные суммы вида
являются формальные суммы вида
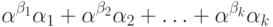
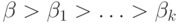 и
и 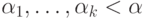 ) с естественным порядком на
них.
) с естественным порядком на
них.Теперь уже понятно, как устроены ординалы в последовательности
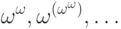
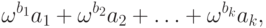
 и
и 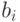 - натуральные числа (и
- натуральные числа (и 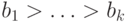 ).
Если в качестве
).
Если в качестве  разрешить писать любые " одноэтажные"
выражения указанного вида, то полученные " двухэтажные" выражения
упорядочены по типу
разрешить писать любые " одноэтажные"
выражения указанного вида, то полученные " двухэтажные" выражения
упорядочены по типу 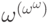 . Разрешив в
показателях
двухэтажные выражения, мы получим трехэтажные выражения, которые образуют
следующий ординал и т.д Если объединить все эти множества, то есть не
ограничивать число этажей (которое для каждого выражения тем не
менее конечно), то получится множество, упорядоченное по типу
. Разрешив в
показателях
двухэтажные выражения, мы получим трехэтажные выражения, которые образуют
следующий ординал и т.д Если объединить все эти множества, то есть не
ограничивать число этажей (которое для каждого выражения тем не
менее конечно), то получится множество, упорядоченное по типу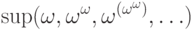
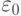 .
.140. Докажите, что
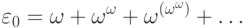
141. Определим для натуральных чисел операцию " тотальной замены
основания  на
на  " (здесь
" (здесь  и
и  - натуральные
числа, причем
- натуральные
числа, причем  )
следующим образом: данное число
)
следующим образом: данное число  запишем в
запишем в  -
ичной системе, то есть
разложим по степеням
-
ичной системе, то есть
разложим по степеням  , показатели степеней снова запишем в
, показатели степеней снова запишем в  - ичной
системе, новые показатели также разложим и т.д. Затем на всех уровнях
заменим основание
- ичной
системе, новые показатели также разложим и т.д. Затем на всех уровнях
заменим основание  на основание
на основание  и вычислим
значение получившегося
выражения. Докажите, что начав с любого
и вычислим
значение получившегося
выражения. Докажите, что начав с любого  и выполняя
последовательность
операций " вычитание
единицы - тотальная замена основания
и выполняя
последовательность
операций " вычитание
единицы - тотальная замена основания  на
на  -
вычитание единицы - тотальная замена основания
-
вычитание единицы - тотальная замена основания  на
на  -
вычитание единицы - тотальная замена основания
-
вычитание единицы - тотальная замена основания  на
на 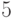 -,
-,  ",
мы рано или поздно зайдем в тупик,т.е.
получится нуль и вычесть единицу будет
нельзя. (Указание: заменим все основания сразу на ординал
",
мы рано или поздно зайдем в тупик,т.е.
получится нуль и вычесть единицу будет
нельзя. (Указание: заменим все основания сразу на ординал  ;
получится
убывающая последовательность ординалов, меньших
;
получится
убывающая последовательность ординалов, меньших 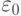 .)
.)
