Индуктивные определения и степени
Теорема 40.
Указанное правило задает полный порядок на множестве ![[B\to A]](/sites/default/files/tex_cache/dbea59e56a8b322788914be99997bd18.png) и порядковый тип этого множества есть
и порядковый тип этого множества есть 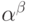 .
.
Доказательство. Нам надо проверить, что указанный порядок является полным и что выполнены требования индуктивного определения степени.
Назовем носителем
элемента ![f\hm\in[B\to A]](/sites/default/files/tex_cache/36e14a481309a5694bcc3cadcd7980f7.png) множество
тех
множество
тех 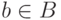 , для которых
, для которых 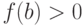 (здесь
(здесь  обозначает
наименьший элемент множества
обозначает
наименьший элемент множества  ). Назовем рангом
функции
). Назовем рангом
функции  наибольший элемент носителя (по определению носитель
конечен, так что наибольший элемент существует). Ранг определен
для всех функций, кроме тождественно нулевой, которая является
минимальным элементом множества
наибольший элемент носителя (по определению носитель
конечен, так что наибольший элемент существует). Ранг определен
для всех функций, кроме тождественно нулевой, которая является
минимальным элементом множества ![[B\to A]](/sites/default/files/tex_cache/dbea59e56a8b322788914be99997bd18.png) . Чем больше ранг
функции, тем больше сама функция в смысле введенного нами
порядка.
. Чем больше ранг
функции, тем больше сама функция в смысле введенного нами
порядка.
Пусть порядок на ![[B\to A]](/sites/default/files/tex_cache/dbea59e56a8b322788914be99997bd18.png) не является полным и
не является полным и  - убывающая последовательность
элементов
- убывающая последовательность
элементов ![[B\to A]](/sites/default/files/tex_cache/dbea59e56a8b322788914be99997bd18.png) . Все элементы
. Все элементы 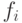 отличны
от
отличны
от  ;
рассмотрим их ранги. Эти ранги образуют невозрастающую
последовательность, поэтому начиная с некоторого места
стабилизируются (множество
;
рассмотрим их ранги. Эти ранги образуют невозрастающую
последовательность, поэтому начиная с некоторого места
стабилизируются (множество  вполне упорядочено). Отбросим
начальный отрезок и будем считать, что с самого начала ранги
всех элементов убывающей последовательности одинаковы и равны
некоторому
вполне упорядочено). Отбросим
начальный отрезок и будем считать, что с самого начала ранги
всех элементов убывающей последовательности одинаковы и равны
некоторому  . В соответствии с определением, значения
. В соответствии с определением, значения  образуют невозрастающую последовательность,
поэтому начиная с некоторого места стабилизируются. Отбросив
начальный отрезок, будем считать, что все
образуют невозрастающую последовательность,
поэтому начиная с некоторого места стабилизируются. Отбросив
начальный отрезок, будем считать, что все 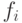 имеют одинаковый
ранг
имеют одинаковый
ранг  и одинаковое значение
и одинаковое значение 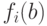 . Тогда
значения
. Тогда
значения 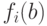 не влияют на сравнения, и потому их можно заменить на
не влияют на сравнения, и потому их можно заменить на  .
Получим убывающую последовательность элементов
.
Получим убывающую последовательность элементов ![[B\to A]](/sites/default/files/tex_cache/dbea59e56a8b322788914be99997bd18.png) с
рангами меньше
с
рангами меньше  . Чтобы завершить рассуждение, остается
сослаться на принцип индукции по множеству
. Чтобы завершить рассуждение, остается
сослаться на принцип индукции по множеству  .
.
(Более формально, рассмотрим все бесконечно убывающие
последовательности. У каждой из них рассмотрим ранг первого
элемента. Рассмотрим те из них, у которых этот ранг минимально
возможный; пусть  - это минимальное значение. В любой такой
последовательности все элементы имеют ранг
- это минимальное значение. В любой такой
последовательности все элементы имеют ранг  . Из всех таких
последовательностей
. Из всех таких
последовательностей 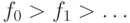 выберем ту, у которой
значение
выберем ту, у которой
значение 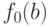 минимально; все следующие ее члены имеют то же
значение в точке
минимально; все следующие ее члены имеют то же
значение в точке  (т.е.
(т.е. 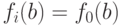 ). Заменив
значение в
точке
). Заменив
значение в
точке  нулем, получим бесконечную убывающую
последовательность из элементов меньшего ранга, что противоречит
предположению.)
нулем, получим бесконечную убывающую
последовательность из элементов меньшего ранга, что противоречит
предположению.)
Теперь покажем, что такое явное определение степени согласовано
с индуктивным определением. Для конечных  это очевидно.
Пусть
это очевидно.
Пусть 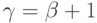 . Каково (явное)
определение
. Каково (явное)
определение 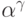 ?
Пусть
?
Пусть  упорядочено по типу
упорядочено по типу  . Тогда мы должны
добавить
к
. Тогда мы должны
добавить
к  новый наибольший элемент (обозначим его
новый наибольший элемент (обозначим его  ) и
рассмотреть отображения
) и
рассмотреть отображения  с конечным носителем.
Ясно, что такое отображение задается парой, состоящей из его
сужения на
с конечным носителем.
Ясно, что такое отображение задается парой, состоящей из его
сужения на  (которое может быть произвольным элементом
множества
(которое может быть произвольным элементом
множества ![[B\to A]](/sites/default/files/tex_cache/dbea59e56a8b322788914be99997bd18.png) ) и значения на
) и значения на  . При определении
порядка
мы сначала сравниваем значения на
. При определении
порядка
мы сначала сравниваем значения на  , а потом сужения
на
, а потом сужения
на  ,
то есть полученное множество изоморфно
,
то есть полученное множество изоморфно ![[B\to A]\hm\times A](/sites/default/files/tex_cache/c9553d015f91ca5cb7d030dd7c2fd0b4.png) , что
и требовалось.
, что
и требовалось.
Пусть теперь  - ненулевой предельный ординал и
множество
- ненулевой предельный ординал и
множество  упорядочено
по типу
упорядочено
по типу  . Как устроено множество
. Как устроено множество ![{[C\to A]}](/sites/default/files/tex_cache/996a6858560b0b600d27d90590bf5e5a.png) ?
Элементы, ранг которых меньше
?
Элементы, ранг которых меньше 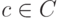 , образуют в нем
начальный отрезок, и этот начальный отрезок изоморфен
, образуют в нем
начальный отрезок, и этот начальный отрезок изоморфен ![[[0,c)\to
A]](/sites/default/files/tex_cache/ee8686681c50f311f03f23f3a6d8359a.png) .
А само множество
.
А само множество ![[C\to A]](/sites/default/files/tex_cache/6a66a86b73dc0c1c8de90d0bf535c647.png) является
объединением этих начальных отрезков (поскольку каждый элемент этого множества
имеет конечный носитель) и потому его
порядковый тип является точной верхней гранью их
порядковых типов, что и требовалось.
является
объединением этих начальных отрезков (поскольку каждый элемент этого множества
имеет конечный носитель) и потому его
порядковый тип является точной верхней гранью их
порядковых типов, что и требовалось.
Непосредственным следствием этой теоремы является такое утверждение:
Теорема 41.Если  и
и  - счетные ординалы, то
- счетные ординалы, то  ,
, 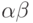 и
и 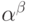 счетны.
счетны.
Доказательство. Для суммы и произведения утверждение очевидно.
Для степени: если мы пронумеровали все элементы вполне упорядоченных
множеств  и
и  , то любой элемент
множества
, то любой элемент
множества ![[B\to A]](/sites/default/files/tex_cache/dbea59e56a8b322788914be99997bd18.png) может быть задан конечным списком натуральных
чисел (носитель и значения на элементах носителя),
а таких списков счетное число.
может быть задан конечным списком натуральных
чисел (носитель и значения на элементах носителя),
а таких списков счетное число.
133. Докажите, что  двумя
способами: по индукции и с использованием явного определения степени.
двумя
способами: по индукции и с использованием явного определения степени.
134. Докажите, что  .
.
135. Докажите, что если  , то
, то  .
.
136. Докажите, что если 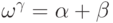 для некоторых
ординалов
для некоторых
ординалов  ,
,  и
и  , то
либо
, то
либо  , либо
, либо 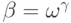 .
.
137. Какие ординалы нельзя представить в виде суммы двух меньших ординалов?
138. Докажите счетность 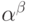 для счетных
для счетных  и
и  ,
используя индуктивное определение степени.
,
используя индуктивное определение степени.
139. Дан некоторый ординал  . Укажите наименьший
ординал
. Укажите наименьший
ординал  , для которого
, для которого 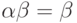 .
(Указание: что будет, если умножить
.
(Указание: что будет, если умножить  на степенной
ряд
на степенной
ряд 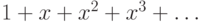 ?)
?)
Отметим важную разницу между операцией возведения ординалов
в степень и ранее рассмотренными операциями сложения и умножения
ординалов. Определяя сумму и произведение ординалов,
мы вводили некоторый
порядок на сумме и произведении соответствующих
множеств (в
обычном смысле), здесь же само множество ![{[B\to A]}](/sites/default/files/tex_cache/ecd3b667b7dd946b6e3570b9355f472c.png) определяется с
учетом порядка и отлично от
определяется с
учетом порядка и отлично от 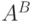 . (В частности,
при счетных
. (В частности,
при счетных  и
и  множество
множество ![{[B\hm\to A]}](/sites/default/files/tex_cache/aee1f1af1012406670e245e6d245ea62.png) счетно, а
счетно, а 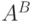 - нет.)
- нет.)
Явное описание множества ![[B\to A]](/sites/default/files/tex_cache/dbea59e56a8b322788914be99997bd18.png) позволяет понять, как
устроены его начальные отрезки, то есть какой вид имеют
ординалы, меньшие
позволяет понять, как
устроены его начальные отрезки, то есть какой вид имеют
ординалы, меньшие 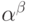 .
.
Рассмотрим некоторую функцию ![f\hm\in [B\to A]](/sites/default/files/tex_cache/94199aaf915fce56e88e984989755511.png) . Пусть она
отлична от нуля в точках
. Пусть она
отлична от нуля в точках  и принимает
там значения
и принимает
там значения  ,
,  ,
,  ,
, 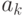 . Нас интересуют все
функции, меньшие функции
. Нас интересуют все
функции, меньшие функции  .
.
Все они равны нулю в точках, больших 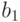 . В самой
точке
. В самой
точке 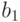 они могут быть либо меньше
они могут быть либо меньше  , либо равны
, либо равны  . Любая
функция первого типа меньше любой функции второго типа. Функции
первого типа могут принимать любые значения в точках,
меньших
. Любая
функция первого типа меньше любой функции второго типа. Функции
первого типа могут принимать любые значения в точках,
меньших 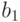 , а
в точке
, а
в точке 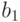 имеют значение из
имеют значение из 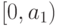 . Тем самым их
можно отождествить с элементами множества
. Тем самым их
можно отождествить с элементами множества ![[[0,b_1)\to A]\hm\times
[0,a_1)](/sites/default/files/tex_cache/be5fc4868bdb56cc1e8954706de8b221.png) , и при этом отождествлении сохраняется
порядок.
, и при этом отождествлении сохраняется
порядок.
Функции второго типа (равные  в точке
в точке 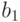 )
снова
разбиваются на две категории: те, которые в точке
)
снова
разбиваются на две категории: те, которые в точке 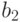 меньше
меньше  и
те, которые в
и
те, которые в 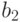 равны
равны  . Функции первой категории
отождествляются с элементами множества
. Функции первой категории
отождествляются с элементами множества ![[[0,b_2)\to A]\hm\times [0,a_2)](/sites/default/files/tex_cache/a49b3b26caa205d910e5e550dc2bc4a9.png) .
Функции второй категории снова разобьем на части в зависимости
от их значения в точке
.
Функции второй категории снова разобьем на части в зависимости
от их значения в точке 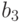 и т.д Таким образом,
и т.д Таким образом, 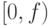 как
упорядоченное множество изоморфно множеству
как
упорядоченное множество изоморфно множеству
![\begin{align*}
[[0,b_1)\to A]\times [0,a_1)&+ [[0,b_2)\to A]\times [0,a_2)+\ldots+\\
&+[[0,b_k)\to A]\times [0,a_k).
\end{align*}](/sites/default/files/tex_cache/6c319d4c22597460ed55e92dc53f24f0.png)
