Теорема Кантора
Классический пример неравномощных бесконечных множеств (до сих пор такого примера у нас не было!) дает " диагональная конструкция Кантора".
Теорема Кантора
Множество бесконечных последовательностей нулей и единиц несчетно.
Доказательство
Предположим, что оно счетно. Тогда все последовательности нулей
и единиц можно перенумеровать: 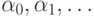 Составим бесконечную вниз таблицу, строками которой будут наши
последовательности:
Составим бесконечную вниз таблицу, строками которой будут наши
последовательности:
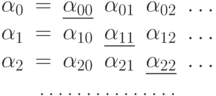
 мы обозначаем
мы обозначаем  -й член
-й член  -й
последовательности). Теперь рассмотрим последовательность,
образованную стоящими на диагонали членами
-й
последовательности). Теперь рассмотрим последовательность,
образованную стоящими на диагонали членами 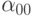 ,
,  ,
,  ,
,  ; ее
; ее  -й член есть
-й член есть 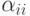 и
совпадает с
и
совпадает с  -м членом
-м членом  -й последовательности.
Заменив все члены на противоположные, мы получим
последовательность
-й последовательности.
Заменив все члены на противоположные, мы получим
последовательность  , у которой
, у которой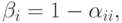
 отличается от любой из
последовательностей
отличается от любой из
последовательностей 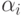 (в позиции
(в позиции  ) и потому
отсутствует в
таблице. А мы предположили, что таблица включает в себя все
последовательности - противоречие.
) и потому
отсутствует в
таблице. А мы предположили, что таблица включает в себя все
последовательности - противоречие.Из этой теоремы следует, что
множество  действительных
чисел (которое, как мы видели, равномощно множеству
последовательностей нулей и единиц) несчетно. В частности, оно
не может совпадать со счетным множеством алгебраических чисел и
потому существует действительное число, не являющееся
алгебраическим (не являющееся корнем никакого ненулевого многочлена
с целочисленными коэффициентами). Такие числа называют трансцендентными.
действительных
чисел (которое, как мы видели, равномощно множеству
последовательностей нулей и единиц) несчетно. В частности, оно
не может совпадать со счетным множеством алгебраических чисел и
потому существует действительное число, не являющееся
алгебраическим (не являющееся корнем никакого ненулевого многочлена
с целочисленными коэффициентами). Такие числа называют трансцендентными.
К моменту создания Кантором теории множеств уже было
известно,
что такие числа существуют. Первый пример такого числа построил
в 1844 году французский математик Ж.Лиувилль. Он
показал, что число, хорошо приближаемое рациональными, не может
быть алгебраическим (таково, например, число 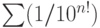 ).
Доказательство теоремы Лиувилля не очень сложно, но все-таки
требует некоторых оценок погрешности приближения; на его фоне
доказательство Кантора, опубликованное им в 1874 году, выглядит
чистой воды фокусом. Эта публикация была первой работой
по теории множеств; в ее первом параграфе доказывается
счетность множества алгебраических чисел, а во втором - несчетность
множества действительных чисел. (Общее определение равномощности
было дано Кантором лишь через три года, одновременно с доказательством
равномощности пространств разного числа измерений, о котором мы
уже говорили.)
).
Доказательство теоремы Лиувилля не очень сложно, но все-таки
требует некоторых оценок погрешности приближения; на его фоне
доказательство Кантора, опубликованное им в 1874 году, выглядит
чистой воды фокусом. Эта публикация была первой работой
по теории множеств; в ее первом параграфе доказывается
счетность множества алгебраических чисел, а во втором - несчетность
множества действительных чисел. (Общее определение равномощности
было дано Кантором лишь через три года, одновременно с доказательством
равномощности пространств разного числа измерений, о котором мы
уже говорили.)
Отметим кстати, что в том же 1874 году французский математик
Ш.Эрмит доказал, что основание
натуральных логарифмов  трансцендентно, а через восемь лет
немецкий математик Ф.Линдеман
доказал трансцендентность числа
трансцендентно, а через восемь лет
немецкий математик Ф.Линдеман
доказал трансцендентность числа  и тем самым невозможность
квадратуры круга.
и тем самым невозможность
квадратуры круга.
В нескольких следующих задачах мы предполагаем известными некоторые начальные сведения из курса математического анализа.
54. Покажите, что для всякого несчетного множества 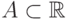 можно указать точку
можно указать точку  , любая окрестность которой пересекается
с
, любая окрестность которой пересекается
с  по несчетному множеству. (Утверждение остается верным,
если слова " несчетное множество" заменить на " множество
мощности континуума".)
по несчетному множеству. (Утверждение остается верным,
если слова " несчетное множество" заменить на " множество
мощности континуума".)
55. Покажите, что любое непустое замкнутое множество 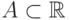 без
изолированных точек имеет мощность континуума.
без
изолированных точек имеет мощность континуума.
56. Покажите, что любое замкнутое множество 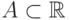 либо
конечно, либо счетно, либо имеет мощность континуума. (Указание.
Рассмотрим множество
либо
конечно, либо счетно, либо имеет мощность континуума. (Указание.
Рассмотрим множество 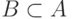 , состоящее из тех
точек множества
, состоящее из тех
точек множества  , в любой окрестности которых несчетно много
других точек из
, в любой окрестности которых несчетно много
других точек из  . Если
. Если  пусто, то
пусто, то  конечно или счетно.
Если
конечно или счетно.
Если  непусто, то оно замкнуто и не имеет изолированных
точек.)
непусто, то оно замкнуто и не имеет изолированных
точек.)
Эта задача показывает, что для замкнутых подмножеств прямой
верна гипотеза континуума, утверждающая,
что любое подмножество
прямой либо конечно, либо счетно, либо равномощно  .
(Кантор, доказавший этот факт,
рассматривал его как первый шаг к доказательству гипотезы
континуума для общего случая, но из этого ничего не вышло.)
.
(Кантор, доказавший этот факт,
рассматривал его как первый шаг к доказательству гипотезы
континуума для общего случая, но из этого ничего не вышло.)
57. Из плоскости выбросили произвольное счетное множество точек. Докажите, что оставшаяся часть плоскости линейно связна и, более того, любые две невыброшенные точки можно соединить двухзвенной ломаной, не задевающей выброшенных точек.
Вернемся к диагональной конструкции. Мы знаем, что множество последовательностей нулей и единиц равномощно множеству подмножеств натурального ряда (каждому подмножеству соответствует его " характеристическая последовательность", у которой единицы стоят на местах из этого подмножества). Поэтому можно переформулировать эту теорему так:
Множество
не равномощно множеству своих подмножеств.
Доказательство также можно шаг за шагом перевести на такой язык:
пусть они равномощны; тогда есть взаимно однозначное
соответствие 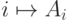 между натуральными числами и
подмножествами натурального ряда. Диагональная
последовательность в этих терминах представляет собой множество
тех
между натуральными числами и
подмножествами натурального ряда. Диагональная
последовательность в этих терминах представляет собой множество
тех  , для которых
, для которых 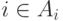 , а
последовательность
, а
последовательность  , отсутствовавшая в перечислении,
теперь будет его дополнением (
, отсутствовавшая в перечислении,
теперь будет его дополнением (  ).
).
При этом оказывается несущественным, что мы имеем дело с натуральным рядом, и мы приходим к такому утверждению:
