НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 6: Численное решение нелинейных алгебраических уравнений и систем

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский физико-технический институт

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3916 / 1197 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00

ISBN: 978-5-9556-0065-9

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Программист, Математик

|

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

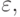Напомним критерий Коши сходимости числовой последовательности: последовательность {u_k}, k = 0, 1, ... является сходящейся, если для любого положительного числа $\varepsilon$ существует номер n такой, что при всех k > N и любых натуральных p расстояние между членами последовательности u_k и u_{k + 1} меньше $\varepsilon,$ т.е. $|u_{k} - u_{k + p}\} | < \varepsilon .$

Напомним критерий Коши для последовательности элементов метрического пространства: последовательность {u_k}, k = 0, 1, ... является сходящейся, если для любого 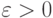$\varepsilon > 0$ существует номер n такой, что при всех k > N и любом натуральном p расстояние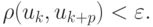 $\rho (u_{k}, u_{k + p}) < \varepsilon.$

Продолжим доказательство. Переходя в последнем неравенстве к пределу при 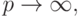$p \to \infty,$ получим

$\rho ({\mathbf{U}}, {\mathbf{u}}_k) \le \rho_0 \frac{q^k}{1 - q}.$

Покажем, что $\mathbf{U}$ есть корень уравнения (5.2)

$\begin{gather*} \rho \left[{{\mathbf{U}}, {\mathbf{F}}({\mathbf{U}})}\right] \le \rho ({\mathbf{U}}, {\mathbf{u}}_{{k + 1}}) + \rho \left[{{\mathbf{u}}_{{k + 1}}, {\mathbf{F}} ({\mathbf{U}})}\right] = \rho ({\mathbf{U}}, {\mathbf{u}}_{{k + 1}}) + \rho \left[ {{\mathbf{F}}({\mathbf{u}}_k), {\mathbf{F}}({\mathbf{U}})}\right] \le \\ \le \rho_0 \frac{q^{k + 1}}{1 - q} + q\rho (\mathbf{u}_k, \mathbf{U}) \le \rho_0 \frac{q^{k + 1}}{1 - q} + q\rho_0 \frac{q^{k}}{1 - q} = 2 \rho_0 \frac{q^{k + 1}}{1 - q} \end{gather*}$

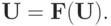
Поскольку k выбрано произвольно, а левая часть от k не зависит, то $\rho \left[{{\mathbf{U}}, {\mathbf{F}}({\mathbf{U}})}\right] = 0,$ или $\mathbf{U} = \mathbf{F}(\mathbf{U}).$

В случае скалярного уравнения имеем 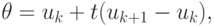$\theta = u_{k} + t(u_{k + 1} - u_{k}),$

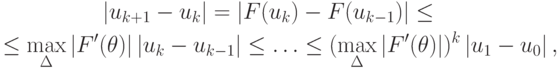
$\begin{gather*} \left|{u_{k + 1} - u_k}\right| = \left|{F(u_k) - F(u_{k - 1})}\right| \le\\ \le \max\limits_\Delta \left|{F^{\prime}(\theta )}\right| \left|{u_k - u_{k - 1}}\right| \le \ldots \le (\max\limits_\Delta \left|{F^{\prime}(\theta )}\right|)^{k} \left|{u_1 - u_0}\right|, \end{gather*}$

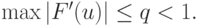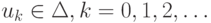
откуда следует условие сходимости итерационного процесса $\max \left|{F^{\prime}(u)}\right| \le q < 1.$ Отрезок $\Delta$ включает в себя всю последовательность { u_k }, $u_k \in \Delta, k = 0, 1, 2, \ldots$

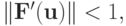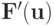В случае решения системы нелинейных уравнений достаточным условием сходимости итерационного процесса будет $\left\|{{\mathbf{F^{\prime}}}({\mathbf{u}})}\right\| < 1,$ где ${\mathbf{F^{\prime}}}({\mathbf{u}})$ — матрица Якоби.

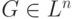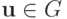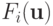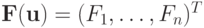Теорема (без доказательства.) Пусть область $G \in L^n$ выпуклая, ${\mathbf{u}} \in G$ а компоненты $F_i(\mathbf{u})$ вектор - функции ${\mathbf{F}}({\mathbf{u}}) = (F_1, \ldots , F_n)^T$ имеют равномерно непрерывные производные первого порядка. Положим, что норма матрицы Якоби

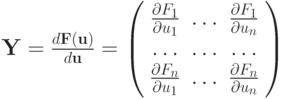
$$ \mathbf{Y} = \frac{d{\mathbf{F}}({\mathbf{u}})}{d{\mathbf{u}}} = \left( \begin{array}{ccc} \frac{\partial F_1}{\partial u_1} & \ldots & \frac{\partial F_1}{\partial u_n} \\ \ldots & \ldots & \ldots \\ \frac{\partial F_n}{\partial u_1} & \ldots & \frac{\partial F_n}{\partial u_n} \\ \end{array} \right)$

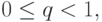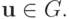
не превосходит некоторого числа $0 \le q < 1,$ т.е. $\left\|{\mathbf{Y}}\right\| \le q < 1$ для всех ${\mathbf{u}} \in G.$

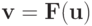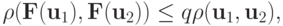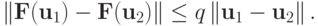
В этом случае отображение ${\mathbf{v}} = \mathbf{F}(\mathbf{u})$ является сжимающим в области G, т.е. $\rho ({\mathbf{F}}({\mathbf{u}}_1 ), {\mathbf{F}}({\mathbf{u}}_2 )) \le q \rho ({\mathbf{u}}_1, {\mathbf{u}}_2 ),$ или $\left\|{{\mathbf{F}}({\mathbf{u}}_1 ) - {\mathbf{F}}({\mathbf{u}}_2 )}\right\| \le q\left\|{{\mathbf{u}}_1 - {\mathbf{u}}_2} \right\|.$

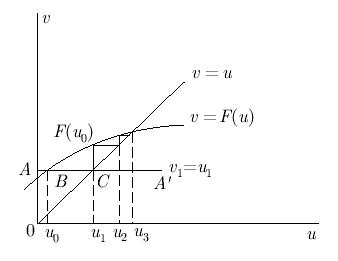
Геометрическая интерпретация метода простой итерации для скалярного случая u_{k + 1} = F(u_k) приведена на рис. 5.1. Алгоритм метода простых итераций таков.

Рис. 5.1. Геометрическая интерпретация метода простых итераций

Локализуем корень, приближенно определяем, на каком отрезке он находится. Вопрос локализации корня не решается алгоритмически, это, скорее, вопрос искусства вычислителя, хотя во многих случаях локализовать корень достаточно легко.
Выбираем точку u₀ на оси 0u.
Вычисляем F(u₀).
Определяем точку u₁ по значению F(u₀):
1. Пересечение горизонтальной прямой AA' с прямой v = u есть точка C (OA = v₁, AC = u₁)
2. Очевидно, что горизонтальная координата точки C и есть u₁ (так как F(u₀) = u₁ ).
3. Опустим перпендикуляр из C на u. Поскольку OA = u₁, то u₁ — значение на первой итерации.
Аналогично строим точки u₂, u₃. Получившаяся диаграмма носит название лесенка Ламерея.

Метод релаксации. Без ограничения общности рассмотрим скалярный случай. Положим 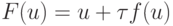$F(u) = u + \tau f(u)$ и построим итерационный процесс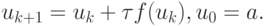 $u_{k + 1} = u_{k} + \tau f(u_{k}), u_{0} = a.$

Тогда 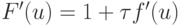$F'(u) = 1 + \tau f'(u)$ и $\tau$ выбирается из условия |F'(u)| < 1, причем, чем меньше значение |F'(u)|, тем быстрее будет сходиться итерационный процесс. В частности, если положить F'(u) = 0, то, $\tau = - [f'(u)]^{ - 1},$ а формулы итерационного процесса будут u_{k + 1} = u_k - [f'(u_k)]^{- 1} f(u_k), u₀ = a.

Дальше >>

Авторизоваться

Введение в вычислительную математику

Численное решение нелинейных алгебраических уравнений и систем

Вопросы и ответы