НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 6: Численное решение нелинейных алгебраических уравнений и систем

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский физико-технический институт

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3916 / 1197 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00

ISBN: 978-5-9556-0065-9

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Программист, Математик

|

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Рассматриваются численные методы решения нелинейных уравнений и систем. На основе принципа сжимающих отображений рассматриваются условия сходимости итерационных методов. Доказывается квадратичная сходимость метода Ньютона. Рассматривается задача о динамике простейшего нелинейного дискретного отображения - логистического. Дается понятие о бифуркациях дискретного отображения.

Ключевые слова: евклидово пространство, итерации, ПО, множества, отображение, функция, расстояние, теорема о неподвижной точке, доказательство, отрезок, системы нелинейных уравнений, матрица Якоби, вектор, производные, норма, интерпретация, метод простой итерации, алгоритм, значение, метод Ньютона, Метод касательных, место, невязки, выражение, погрешность, равенство, Метод секущих, параметр, метод наискорейшего спуска, обратная функция, дискретные отображения, процент, метод Эйлера, обобщение, интервал, неподвижная точка, траектория, устойчивость, определение, цикла, бифуркации, график, прямой, закономерность, диаграмма, элемент цикла, отношение, предел, симметричная функция, чередование, численное решение уравнений

5.1. Сжимающие отображения. Итерации. Метод простых итераций (МПИ)

Рассмотрим системы нелинейных алгебраических уравнений, записанные в векторном виде.

Система нелинейных алгебраических уравнений

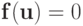${\mathbf{f(u)} = 0}$

( 5.1)

может быть также представлена в равносильном виде

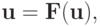$\mathbf{u} = \mathbf{F(u)},$

( 5.2)

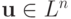где ${\mathbf{u}} \in L^n$ L_n — n - мерное евклидово пространство. Как правило, для нелинейной системы переход от формы записи (5.1) к равносильному виду (5.2) осуществляется не единственным образом.

Поставим в соответствие системе (5.2) итерационный процесс, определяющий последовательность итераций (последовательных приближений к решению) . Соответствующий итерационный процесс записывается в форме

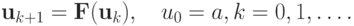${\mathbf{u}}_{k + 1} = {\mathbf{F}}({\mathbf{u}}_k), \quad u_0 = a, k = 0, 1, \ldots .$

( 5.3)

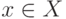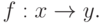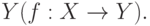Для дальнейшего изложения потребуется понятие отображения. Отображением называется закон, по которому каждому элементу x некоторого множества X однозначно сопоставляется определенный элемент y множества Y ( X может совпадать с Y ). 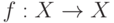Это соотношение между элементами $x \in X$ и $y \in Y$ записывается как y = f(x) или $f: x \rightarrow y.$ Говорят, что отображение f действует из X в $Y (f: X \rightarrow Y).$ Отображение $f: X \rightarrow X$ называют преобразованием множества X, это отображение f преобразует множество X в себя. В функциональном анализе и линейной алгебре вместо термина "отображение" часто употребляется термин "оператор", в случае, если X и Y — числовые множества, употребляется термин "функция".

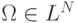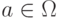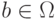Определение. Область $\Omega \in L^{N}$ называется выпуклой, если наряду с любыми двумя точками $a \in \Omega$ и $b \in \Omega$ она включает все точки отрезка [a, b], т.е. точки с координатами u = a + t(b - a), где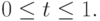 $0 \le t \le 1.$

Определение. Отображение 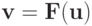${\mathbf{v}} = {\mathbf{F}}({\mathbf{u}})$ называется сжимающим в замкнутой выпуклой области $\Omega,$ если существует такое число 0 < q < 1, что

$\rho \left[{{\mathbf{F}}({\mathbf{u}}_1 ), {\mathbf{F}}({\mathbf{u}}_2 )}\right] \le q\rho ({\mathbf{u}}_1, {\mathbf{u}}_2 )$

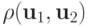при любых u₁, u₂, принадлежащих области $\Omega,$ здесь $\rho(\mathbf{u}_1, \mathbf{u}_2)$ — расстояние между элементами. В линейном нормированном пространстве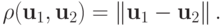 $\rho ({\mathbf{u}}_1, {\mathbf{u}}_2 ) = \left\|{{\mathbf{u}}_1 - {\mathbf{u}}_2}\right\|.$

Приведем без доказательства одну из основных теорем функционального анализа.

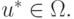
Теорема (принцип сжимающих отображений). Всякое сжимающее отображение имеет в $\Omega$ одну и только одну неподвижную точку $u^{*} \in \Omega.$

Более подробно о сжимающих отображениях и другие теоремы о неподвижных точках можно найти, например, в [5.1], [5.2], [5.3].

Теорема (о сжимающем отображении [5.1], [5.5].)

Последовательность 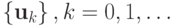$\left\{{{\mathbf{u}}_k}\right\}, k = 0, 1, \ldots$ элементов n - мерного евклидова пространства, порожденная итерационным процессом

${\mathbf{u}}_{{k + 1}} = {\mathbf{F}}({\mathbf{u}}_k), {\mathbf{u}}_0 = {\mathbf{a}},$

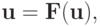сходится к решению $\mathbf{U}$ системы нелинейных алгебраических уравнений $\mathbf{u} = \mathbf{F(u)},$ если отображение

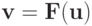
${\mathbf{v}} = {\mathbf{F}}({\mathbf{u}})$

является сжимающим; при этом выполнено

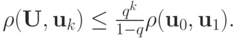
$\rho ({\mathbf{U}}, {\mathbf{u}}_k) \le \frac{q^k}{1 - q}\rho ({\mathbf{u}}_0, {\mathbf{u}}_1 ).$

Доказательство.

По определению сжимающего отображения

$\begin{gather*} \rho ({\mathbf{u}}_{k + 1}, {\mathbf{u}}_k) = \rho \left[{{\mathbf{F}}({\mathbf{u}}_k), {\mathbf{F}}({\mathbf{u}}_{k - 1})}\right] \le \\ \le q\rho ({\mathbf{u}}_k, {\mathbf{u}}_{k - 1}) \le \ldots \le q^k \rho ({\mathbf{u}}_0, {\mathbf{u}}_1 ) = q^k \rho_0 . \end{gather*}$

В таком случае получим цепочку неравенств при p > k:

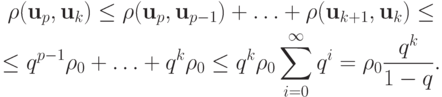
$\begin{gather*} \rho ({\mathbf{u}}_p, {\mathbf{u}}_k) \le \rho ({\mathbf{u}}_p, {\mathbf{u}}_{p - 1}) + \ldots + \rho ({\mathbf{u}}_{k + 1}, {\mathbf{u}}_k) \le \\ \le q^{p - 1}\rho_0 + \ldots + q^k \rho_0 \le q^k \rho_0 \sum\limits_{i = 0}^\infty q^i = \rho_0 \frac{q^k}{1 - q}. \end{gather*}$

В соответствии с критерием Коши существования предела последовательности, последовательность { 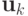$\mathbf{u}_k$ } стремится к пределу 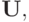$\mathbf{U},$ поскольку правая часть неравенства стремиться к нулю при $k \to \infty.$

Дальше >>

Авторизоваться

Введение в вычислительную математику

Численное решение нелинейных алгебраических уравнений и систем

5.1. Сжимающие отображения. Итерации. Метод простых итераций (МПИ)

Вопросы и ответы