Численное решение нелинейных алгебраических уравнений и систем
5.3. О вариационных подходах к решению нелинейных систем уравнений
Рассмотрим систему нелинейных уравнений f(u, v) = 0, g(u, v) = 0, 
Рассмотрим функционал 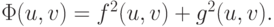
Так как  неотрицателен, то найдется точка
неотрицателен, то найдется точка  такая, что
такая, что  но
но 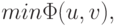 очевидно, достигается при f(u, v) = 0, g(u, v) = 0, т.е. на решении исходной системы уравнений.
очевидно, достигается при f(u, v) = 0, g(u, v) = 0, т.е. на решении исходной системы уравнений.
Построим итерационный процесс, соответствующий методу градиентного спуска
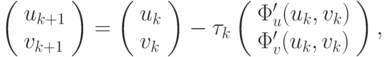
где  — параметр, который выбирается, например, из условия минимальности
— параметр, который выбирается, например, из условия минимальности 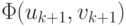 в данном направлении (метод наискорейшего спуска), {pk, qk} — вектор,
определяющий направление минимизации. На каждом шаге итераций решается задача минимизации
в данном направлении (метод наискорейшего спуска), {pk, qk} — вектор,
определяющий направление минимизации. На каждом шаге итераций решается задача минимизации  по одному аргументу.
по одному аргументу.
5.4. Метод Чебышёва построения итерационных процессов высшего порядка
Предположим, что существует функция g(u), обратная к f(u). При этом u = g[f(u)], U = g(0). Пусть, кроме того, f(u) непрерывна и имеет необходимое число непрерывных производных на отрезке, внутри которого лежат все члены последовательности {uk}, k = 0, 1, ... Обратная функция имеет такое же количество непрерывных производных, как и f(u). Разложим функцию g(f[v]) = g(h) в ряд Тейлора в окрестности корня - точки w = f(u)

Тогда, учитывая, что u = g[f(u)], w = f(u), h = f(v), получим
![$ g(0) = U \approx u + \sum\limits_{i = 1}^{n}{\frac{{g^{i}[f(u)]}}{{i!}}} [- f(u)]^{i} + \ldots. $](/sites/default/files/tex_cache/120e7e79fa9ccb65876ea82312837da8.png)
Можно показать, что итерационный метод
![$ u_{k + 1} = u_k + \sum\limits_{i = 1}^{n}(- 1)^{i}
\frac{g^{(i)} \left[{f(u_k)}\right]}{i!}[f(u_k)]} ^{i}, u^0 = a $](/sites/default/files/tex_cache/67b94ed7eae912527e7b6ca7b1e8bd2d.png)
имеет порядок сходимости n + 1. Для вычисления производных обратной функции u = g[f(u)] воспользуемся правилом дифференцирования сложной функции:
![\begin{gather*}
1 = g^{(1)} [f(u)] \cdot f^{(1)} (u), \\
0 = g^{(2)} [f(u)] \cdot [f^{(1)} (u)]^2 + g^{(1)} [f(u)]\cdot f_{(u)}^{(2)}, \\
0 = g^{(3)} [f(u)] \cdot [f_{(u)}^{(1)} ]^3 + 3g^{(2)} [f(u)]\cdot f_{(u)}^{(2)} \cdot f_{(u)}^{(1)} + g^{(1)} [f(u)]\cdot f_{(u)}^{(3)}, \\
\ldots
\end{gather*}](/sites/default/files/tex_cache/ee5f043b215db87855bc7ea9f06de9f2.png)
5.5. Разностные отображения в нелинейной динамике
Рассмотрим последовательность чисел  ( R — множество вещественных чисел), каждый член которой связан с предыдущим рекуррентным соотношением
( R — множество вещественных чисел), каждый член которой связан с предыдущим рекуррентным соотношением
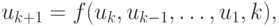 |
( 5.4) |
где 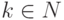 ( N — множество натуральных
чисел). Соотношения (5.4) называются разностными отображениями (уравнениями) с дискретным аргументом.
( N — множество натуральных
чисел). Соотношения (5.4) называются разностными отображениями (уравнениями) с дискретным аргументом.
Такие уравнения появляются при моделировании процессов, в которых величина u рассматривается через определенные промежутки времени. Например, еще в середине XIX века Ферхюльст для описания динамики популяционной системы предложил измерять ежегодно численность особей uk, где k — номер года. Относительная численность uk + 1 полагалась пропорциональной численности в k год, однако она начинает убывать, когда животных становится много ( uk сравнимо с 1):
 |
( 5.5) |
где
 |
( 5.6) |
Другой пример из экономической области — задача о банковских сбережениях. Пусть u0 — денежный вклад, растущий в соответствии с постоянным процентом 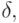 по закону:
по закону:

Пусть далее законодательный орган, желая воспрепятствовать такому обогащению вкладчика, издает закон о том, чтобы процент убывал пропорционально uk, т.е.

