НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 11: Численное решение краевых задач для систем обыкновенных дифференциальных уравнений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский физико-технический институт

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3914 / 1195 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00

ISBN: 978-5-9556-0065-9

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Программист, Математик

|

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Рассматриваются численные методы решения краевых задач. На примере линейных краевых задач иллюстрируется применение различных вариантов метода прогонки — дифференциальной прогонки, разностной трехточечной прогонки, пятиточечной прогонки, матричной прогонки, периодической прогонки. Для нелинейных краевых задач рассмотрены методы стрельбы и квазилинеаризации. Дается представление о методах решения спектральных задач (задач на собственные значения). Обсуждается вопрос о применении метода Фурье при решении краевых задач для разностных уравнений, аппроксимирующих исходную дифференциальную задачу.

Ключевые слова: единица, функция, частное решение, коэффициенты, метод трапеций, характеристическое уравнение, поток, погрешность, дифференциальная прогонка, равенство, жесткие краевые задачи, параметр, матрица, отношение, класс, задача Штурма-Лиувилля, численное решение уравнений, Главная диагональ, метод прогонки, запись, прямой, обратный, алгоритм, устойчивость, вычисление, место, обобщение, вектор, матричная прогонка, метод стрельбы, численное дифференцирование, дифференциальное уравнение, интегрирование, Метод касательных, значение, задача Коши, сходимость, коэффициенты Фурье, выражение, деление, метод Фурье, шаг вычислений, спектральные задачи

10.1. Краевая задача для линейной системы ОДУ первого порядка

Рассмотрим линейную систему ОДУ первого порядка

$\frac{du}{dt} = Au + f, u \in R^n, t \in [0, L]$

с краевыми условиями

Ru(0) + Su(L) = q,

где u, f, q — n - мерные векторы, A(t), R(t), S(t) — матрицы размера n x n.

Для приближенного решения задачи введем расчетную сетку 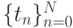$\{t_n\}_{n = 0}^{N}$ и за приближенное решение примем сеточную функцию 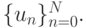$\{u_n\}_{n = 0}^{N}.$ Рассмотрим методы построения приближенного решения.

Метод построения фундаментальных решений аналогичен известному по курсу дифференциальных уравнений способу построения общего решения системы линейных уравнений первого порядка. Решение представляется в виде

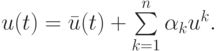
$u(t) = \bar{u}(t) + \sum\limits_{k = 1}^n {\alpha_k u^k}.$

Здесь u_k(t) есть полная фундаментальная система решений однородной задачи

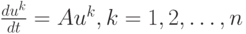
$\frac{{d{u}^{k}}}{dt} = Au ^{k}, k = 1, 2, \ldots , n$

с начальными данными, например,

u^k(0) ={0, ..., 0, 1, 0, ..., 0}^T,

где единица стоит на k месте, т.е. в качестве начальных данных используются векторы u^k(0) = E_k. Важно, чтобы решения однородной задачи составляли систему линейно независимых функций. Каждая такая функция ищется численно как решение соответствующей задачи Коши, используя методы, описанные в "Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений" и "Численные методы решения жестких систем обыкновенных дифференциальных уравнений" .

Пусть 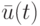$\bar{u}(t)$ — частное решение неоднородной системы

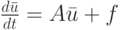
$\frac{d\bar{u}}{dt} = A\bar{u} + f$

с нулевыми начальными условиями 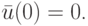$$ \bar{u}(0) = 0 $.$ Тогда неопределенные коэффициенты $\alpha_k$ находятся из краевых условий

$\begin{gather*} Ru(0) + Su(L) = q, \mbox{ или }\\ R[\sum\limits_{k = 1}^n{\alpha_k{u}^k (0)}] + S\bar {u}(L) + S[\sum\limits_{k = 1}^n{\alpha_k{u}^k(L)}] = q. \end{gather*}$

Последнее соотношение представляет собой СЛАУ относительно коэффициентов 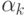$\alpha_{k}$ размерности n.

Полную фундаментальную систему решений однородной задачи можно получить, используя, например, схему второго порядка точности (метод трапеций)

$\begin{gather*} \frac{u_{n + 1} - u_n}{\tau } = A_{n + 1/2}\frac{u_n + u_{n + 1}}{2}, A_{n + 1/2} = A\left({t_n + \frac{\tau }{2}}\right), \\ u_{n + 1} = (E - \frac{\tau}{2} A_{n + 1/2})^{- 1}(E + \frac{\tau}{2}A_{n + 1/2})u_k, \\ u_0 = E_k . \end{gather*}$

Частное решение получаем аналогично:

$\begin{gather*} \frac{\bar{u}_{n + 1} - \bar{u}_n}{\tau } = A_{n + 1/2} \frac{\bar{u}_{n + 1} + \bar{u}^{\prime\prime}_n}{2} + f_{n + 1/2}, \\ f_{n + 1/2} = F\left({t_n + \frac{\tau }{2}}\right), \\ \bar{u}_0 (0) = 0, \mbox{или}\\ \bar{u}_{n + 1} = \left({E - \frac{\tau}{2}A}\right)^{- 1}\left[{\left({E + \frac{\tau}{2}A}\right)u_n + \tau f_{n + 1/2}}\right], \bar{u}_0 = 0. \end{gather*}$

Приведем пример, когда решение задачи методом построения фундаментальных решений не проходит. Рассмотрим систему уравнений

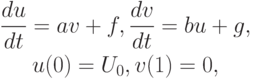
$\begin{gather*} \frac{du}{dt} = {av} + f, \frac{dv}{dt} = bu + g, \\ u(0) = U_0, v(1) = 0 , \end{gather*}$

Подобные системы ОДУ моделируют, например, процессы прохождения излучения или потоков элементарных частиц (гамма - излучение, потоки нейтронов) через разные среды (атмосфера, защита ядерных реакторов) в приближении оптически толстого слоя. Коэффициенты 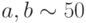$a, b \sim 50$ характерны для защиты реакторов. Найдем общее решение этой задачи с помощью метода фундаментальных систем в виде линейной комбинации двух решений однородных ОДУ:

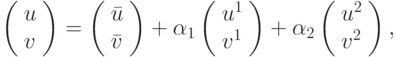
$\left( \begin{array}{l} u \\ v \\ \end{array} \right) = \left( \begin{array}{l} {\bar {u}} \\ {\bar {v}} \\ \end{array} \right) + \alpha_1 \left( \begin{array}{l} u^1 \\ v^1 \\ \end{array} \right) + \alpha_2 \left( \begin{array}{l} u^2 \\ v^2 \\ \end{array} \right),$

где (u₁, v₁) и (u₂, v₂) — решения двух однородных систем (в дальнейшем для простоты будем полагать, что 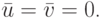$$ \bar {u} = \bar {v} = 0 $.$ ) Тогда

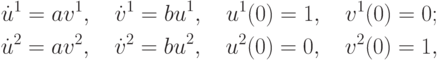
$\begin{gather*} \dot {u}^1 = {av}^1, \quad \dot {v}^1 = {bu}^1, \quad u^1 (0) = 1, \quad v^1 (0) = 0; \\ \dot {u}^2 = {av}^2, \quad \dot {v}^2 = {bu}^2, \quad u^2 (0) = 0, \quad v^2 (0) = 1, \end{gather*}$

а коэффициенты 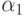$\alpha_1$ и $\alpha_2$ находятся из краевых условий.

Общее решение такой системы, как известно, представляет собой сумму двух экспонент

$\left( \begin{array}{l} u^1 \\ v^1 \\ \end{array} \right) = C_1 \left( \begin{array}{l} a_1 \\ b_1 \\ \end{array} \right)e^{\lambda_1 t} + C_2 \left( \begin{array}{l} a_2 \\ b_2 \\ \end{array} \right)e^{\lambda_2 t}$

(аналогичным образом решение представляется и для u₂, v₂ ), где a_i, b_i, i = 1, 2 находятся из решения задачи, C_i; i = 1, 2 — произвольные постоянные; 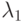$\lambda _{1}$ и $\lambda _{2}$ — корни характеристического уравнения

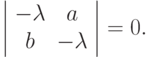
$\left| \begin{array}{cc} {- \lambda} & {a} \\ {b} & {- \lambda} \\ \end{array} \right| = 0.$

Решая характеристическое уравнение, получаем $\lambda_{1, 2} = \pm \sqrt{ab}} \approx \pm 50.$ Полученное решение есть сумма двух экспонент: одной, быстро растущей ( $\sim e^{50t}$ ), и второй, быстро убывающей ( $\sim e^{ - 50t}$ ). Искомое же решение есть функция, близкая к U₀e^{- 50t} (в случае задачи с защитой ректора U₀ — падающий поток нейтронов; задача защиты — значительное его ослабление, приблизительно в e⁵⁰ раз).

Слагаемые с быстрорастущими экспонентами должны взаимно уничтожиться. Получение же численного решения - весьма трудная задача, поскольку численное решение имеет большую и быстро возрастающую погрешность. Пусть 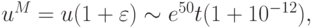$u^{M} = u(1 + \varepsilon ) \sim e^{50}t(1 + 10^{ - 12}),$ т.е. начальная погрешность имеет порядок 10^{- 12}. Она возрастает при вычислениях примерно в e^50t раз — даже при умеренных t это очень большое число.

Дальше >>

Авторизоваться

Введение в вычислительную математику

Лекция 11: Численное решение краевых задач для систем обыкновенных дифференциальных уравнений

10.1. Краевая задача для линейной системы ОДУ первого порядка

Вопросы и ответы