Московский физико-технический институт
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3916 / 1197 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00
ISBN: 978-5-9556-0065-9
Специальности: Программист, Математик
Теги:
Лекция 11: Численное решение краевых задач для систем обыкновенных дифференциальных уравнений
10.7. Краевые задачи на собственные значения для обыкновенных дифференциальных уравнений
Краевые задачи на собственные значения достаточно часто встречаются в физических приложениях. Например, это задача определения собственных колебаний струны, сводящаяся к ОДУ вида
![$ \frac{d}{dt} [k(t)\frac{du}{dt}] + \lambda r(t)u = 0. $](/sites/default/files/tex_cache/13ff5c3e937187d5832aef996e582831.png)
В приведенном уравнении краевые условия зависят от способа закрепления струны.
Это и задачи собственных колебаний упругого стержня (ОДУ четвертого порядка), нахождения энергетических уровней атома водорода, вычисление критических нагрузок в теории стержней и оболочек и др.
В задачах на собственные значения добавляется еще один пристрелочный параметр —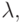 
поэтому эти задачи часто решаются методом стрельбы. Приведем простейший пример — одно дифференциальное уравнение первого порядка с двумя краевыми условиями (второе краевое условие появляется из - за присутствия неизвестного параметра 
):
Если не учитывать правое краевое условие, то получим задачу Коши. Ее численное интегрирование приводит к некому значению на правом конце, зависящему от и, вообще говоря, не равному u2. Варируя параметр 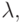можно добиться выполнения правого краевого условия с некоторой заданной точностью. При этом, разумеется, используются методы численного нахождения корней алгебраического уравнения, обычно метод касательных.
Второй пример — краевая задача на собственные значения для ОДУ второго порядка с нулевыми краевыми условиями:
![\begin{gather*}
\frac{d^2 u}{dt^2 } + {b^{\prime}}(t)\frac{du}{dt} + [{c^{\prime}}(t) + \lambda ]u = 0, \\
u(0) = u(L) = 0.
\end{gather*}](/sites/default/files/tex_cache/e5b322c0d9d08270920db7b6f84166a5.png)
Поскольку это уравнение второго порядка с неизвестным параметром (собственное значение дифференциального оператора), то для его решения требуется третье условие. Однако в силу линейности и однородности задачи
решение определяется с точностью до произвольного постоянного множителя, что и является неявным заданием третьего условия. Его можно задать, например, следующим образом:
Трудности при использовании метода стрельбы возникают, если соответствующая задача Коши плохо обусловлена, а также в случае жестких краевых задач. В этих случаях появляется сильная зависимость численного решения от пристрелочного параметра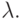 
В качестве тестового примера для сравнения с результатами численного расчета удобно использовать модельную краевую задачу на собственные значения:
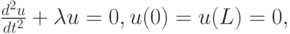
имеющую точное решение
Непосредственной подстановкой показывается, что решениями соответствующей разностной задачи на собственные значения
являются собственные значения и собственные функции
откуда видно, что
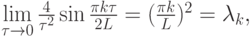
т.е. имеет место сходимость решения разностной задачи к решению дифференциальной задачи 
