НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 11: Численное решение краевых задач для систем обыкновенных дифференциальных уравнений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский физико-технический институт

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3916 / 1197 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00

ISBN: 978-5-9556-0065-9

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Программист, Математик

|

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

10.10. Задачи для самостоятельного решения

Рассмотреть две краевые задачи:
${y^{\prime\prime} = e^{y}, \quad y (0) = a, \quad y (1) = b, }$ ( 10.6)

${y^{\prime\prime} = - e^{y}, \quad y (0) = a , \quad y (1) = b.}$ ( 10.7)
- Найти решения этих задач, положив a = 1 и сделав замену y'_x = p(y).
- Найти решение методом стрельбы при a = 1 и различных b. Что происходит при 0 < b < 1, 499719998? При b > 1,499719998? [10.6, c. 110].
- Решить задачу (10.6) методом Нумерова (10.4) с линеаризацией по Ньютону. Сколько узлов сетки необходимо, чтобы найти решение с точностью $\varepsilon = 10^{ - 4}$ ?
Рассмотреть нелинейную сингулярно - возмущенную^{1Сингулярно - возмущенными задачами называются задачи с малым параметром при старшей производной.} краевую задачу:
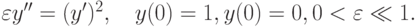
$\varepsilon y^{\prime\prime} = (y^{\prime})^2, \quad y(0) = 1, y(0) = 0, 0 < \varepsilon \ll 1.$
- Получить точное решение задачи [10.8, c. 11]. Для этого следует сделать замену y'_x = p(y).
- Предложить и реализовать численный метод решения задачи. Сравнить полученное решение с точным. Исследовать поведение погрешности численного метода при $\varepsilon \to 0.$
Рассмотрим краевую задачу
$\varepsilon y'' = (y - u(x))^{2q + 1}, \\ y(- 1) = A, y(1) = B,$

где $q \in N$ — натуральное число, $0 < \varepsilon \ll 1.$

Получить численное решение задачи в случаях:
- u(x) = x², A > 1, B> 1,
- u(x) = x², A = 1, B > 1 или A > 1, B = 1,
- u(x) = | x |, A > 1, B > 1,
- u(x) = | x |, A = 1, B > 1.
Что происходит с решением при увеличении q? (В численных расчетах задать $\varepsilon = 10^{ - 2}, 10^{ - 3}, 10^{ - 4}).$

Теоретически задача исследована в [10.8, c. 170 - 171]. В случае u(x) = | x | появляется внутренний пограничный слой — узкая область в окрестности x = 0, где y отличны от | x |.
Решить численно краевую задачу:
$\begin{gather*} \varepsilon y^{\prime\prime} = y - y^3, \\ y(0) = A, \quad y(1) = B, \left|A\right| < \sqrt 2, \quad \left|B\right| < \sqrt 2, \quad 0 < \varepsilon \ll 1. \end{gather*}$

Решением этой задачи являются так называемые пиковые, или пичковые, структуры. В [10.8, с. 171 - 174] исследованы свойства решений и приведены графики восьми линейно независимых решений. Там же показано, что при фиксированных A и B существует по четыре линейно независимых решения, таких, что

$\lim\limits_{\varepsilon \to 0} y(x, \varepsilon ) = 0$
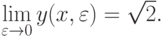
при всех x, за исключением точек $x_i = {i/n}, i = \overline{1, n - 1}, n \in N (n \ge 2),$ где $\lim\limits_{\varepsilon \to 0}y(x, \varepsilon ) = \sqrt 2 .$

Найти численно такие структуры для n = 2, n = 3, выбирая соответствующее начальное приближение при линеаризации по Ньютону. (Положить $\varepsilon = 10^{ - 2}, 10^{ - 3}, 10^{ - 4}$ ).
Известно, что краевая задача
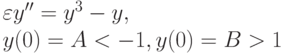
$\varepsilon y'' = y^{3} - y, \\ y(0) = A < - 1, y(0) = B> 1$

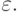
имеет решение с внутренним пограничным слоем в точке x = 1/2 [10.8, c. 175]. Исследовать, как его толщина зависит от параметра $\varepsilon.$

Какое начальное приближение надо использовать при решении задачи методом линеаризации?

Известно, что при A = 0, В = 0 данная краевая задача имеет еще два решения, кроме тривиального ( $y \equiv 0$ ). Найти их численно.

Всего у этой задачи счетное множество решений.
Исследовать следующую сингулярно - возмущенную задачу:
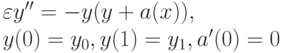
$\varepsilon y'' = - y(y + a(x)), \\ y (0) = y_{0}, y (1) = y_{1}, a'(0) = 0$

в зависимости от вида функции a(x). Рассмотреть поведение решения при $\varepsilon \to 0.$ Удалось ли получить пограничный слой типа всплеска?
Решить численно задачу на нахождение собственных значений и собственных функций волнового уравнения [10.1, c. 180 - 206]:
```
y'' = - k²y,  y (0) = y (1) = 0.
```
- Сравнить полученные решения с известными точными 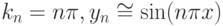$k_n = n\pi , y_n \cong \sin (n\pi x)$ ( n — положительное целое число).
- Использовать этот же алгоритм для получения решения при больших k. С какими трудностями пришлось столкнуться? Как можно улучшить используемый алгоритм?
- Рассмотреть данную задачу для других граничных условий, например, y'(0) = y (1) = 0.
В цилиндрических координатах задача на собственные значения имеет следующий вид:
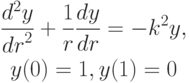
$\begin{gather*} \frac{d^2 y}{{dr}^2 } + \frac{1}{r}\frac{dy}{dr} = - k^2 y, \\ y(0) = 1, y(1) = 0 \end{gather*}$

Собственными функциями этой задачи являются цилиндрические функции Бесселя нулевого порядка, а собственными значениями задачи будут нули этих функций:
```
k₁ = 2, 404826 ,  k₂ = 5, 520078 , 
k₃ = 8, 653728 ,  k₄ = 11, 791538.
```
Показать, что подстановка
$\tilde {y} = \frac{y}{\sqrt{r}}$
приводит уравнение к виду, для которого можно применять метод Нумерова. Решить численно спектральную задачу. Сравнить результаты расчета с точными собственными значениями, приведенными выше.
Частица в потенциальной яме
Найти численно все уровни энергии частицы в потенциальной яме с потенциалом 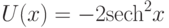$U(x) = - 2{\mathop{\mathrm{sech}}\nolimits}^2 x$ и соответствующие им функции распределения.

Указание: уровни энергии есть собственные значения 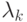$\lambda _{k}$ уравнения Шредингера $y'' + (\lambda - U(x))y = 0$ с условиями $y(+ \infty ) = y(- \infty ) = 0,$ а соответствующие им собственные функции и есть функции распределения.

Данный результат важен для решения уравнения Кортвега - Де Фриза, поэтому обсуждается в [10.9, c. 11 - 17].
Частица в потенциальной яме
- Получить аналитическое решение уравнения Шредингера для случая прямоугольной и параболической потенциальных ям и сравнить его с численными решениями, найденными обычным методом второго порядка аппроксимации с использованием алгоритма прогонки и методом Нумерова.
- Рассмотреть случай, когда потенциал имеет зеркальную симметрию относительно x = 0. При этом собственные функции системы будут четными или нечетными относительно x = 0, причем четность или нечетность чередуется с ростом квантового числа (энергии). Проверить этот эффект численно. Каким способом в этом случае можно в два раза сократить объем вычислений при расчете собственных значений для потенциалов?
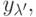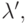- Проверить численно, что для заданного потенциала две волновые функции $y_{\lambda }$ и $y_{\lambda '},$ соответствующие разным собственным значениям $\lambda$ и $\lambda ',$ являются ортогональными: $\int {y_\lambda (x)y_{\lambda ^{\prime}} (x) = 0},$ как это следует из квантовой механики.
Частица в поле с потенциалом Тоды
Рассмотреть движение частицы в поле с потенциалом Тоды ([10.10, c. 87 - 89]):

$\ddot {x} = 1 - e^{x}$
Это уравнение можно трактовать как движение частицы в поле с потенциалом U(x) = e^x - x.

Найти численно все периодические решения, удовлетворяющие следующим граничным условиям:

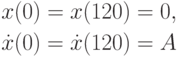
$\begin{gather*} x(0) = x(120) = 0, \\ \dot {x}(0) = \dot {x}(120) = A \end{gather*}$

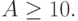
и дополнительному условию $A \ge 10.$

Как период колебаний зависит от A? Сколько решений получается?