Введение в вычислительную математику
[+]
Московский физико-технический институт
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3916 / 1197 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00
ISBN: 978-5-9556-0065-9
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Программист, Математик
Теги: beta, алгебра, алгоритмы, арифметика, вычисления, дифференциальные уравнения, курсы, линейная алгебра, матрица Якоби, метод трапеций, метод Эйлера, норма вектора, поиск, программирование, разделенные разности, разложение в ряд, системы нелинейных уравнений, спектральные задачи, таблицы бутчера, численное решение уравнений, элементы

Лекция 11: Численное решение краевых задач для систем обыкновенных дифференциальных уравнений

A
|
версия для печати
< Лекция 10 || Лекция 11: 123456789

10.2. Метод дифференциальной прогонки. Понятие о жестких краевых задачах

Рассмотрим метод дифференциальной прогонки, не приводя доказательства его устойчивости. Покажем, что с помощью этого метода можно решить рассмотренную выше задачу. Будем искать решение в виде

u(t) = \alpha(t)v (t) + \beta(t),

где \alpha и \beta — пока неизвестные функции (прогоночные коэффициенты), для которых необходимо получить дифференциальные уравнения.

Продифференцируем это соотношение

$ \dot {u} = \dot {\alpha} v + \alpha \dot {v} + \dot {\beta} $

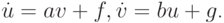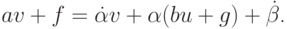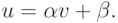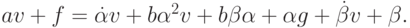
и подставим в него уравнения системы $ \dot {u} = {av} + f, \dot {v} = {bu} + g $. В результате получим, что $ {av} + f = \dot {\alpha} v + \alpha ({bu} + g) + \dot {\beta} $. Подставим в полученное соотношение уравнение u = \alpha v + \beta . Тогда {av} + f = \dot {\alpha} v + b\alpha ^2 v + b\beta \alpha + \alpha g + \dot {\beta} v + \beta .

После приведения подобных членов имеем равенство

$ v(\dot {\alpha} + b\alpha ^2 - a) + (\dot {\beta} + b\beta \alpha + \alpha g - f) = 0. $

Приравнивая к нулю коэффициенты при v и единице, получим два дифференциальных уравнения для прогоночных коэффициентов:

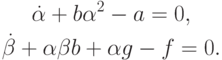
\begin{gather*} \dot {\alpha} + b\alpha^2 - a = 0, \\ \dot {\beta} + \alpha \beta b + \alpha g - f = 0. \end{gather*}

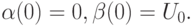Дополним их начальными условиями. Левое краевое условие вида u (0) = U0 запишем в виде прогоночного соотношения u(0) = \alpha (0) v(0) + \beta(0), полагая \alpha (0) = 0, \beta(0) = U_0. Таким образом, получаем начальные данные для двух задач Коши для 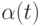\alpha (t) и \beta (t), которые могут быть решены численно.

Теперь разрешим правое краевое условие. На правой границе отрезка интегрирования имеем условие v(1) = 0 и прогоночное соотношение при t = 1: u (1) = \alpha (1)v(1) + \beta (1), откуда получаем u(1) = \beta (1).

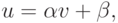Далее воспользуемся уравнением $ \dot {v} = {bu} + g $, подставив в него прогоночное соотношение u = \alpha v + \beta, получим дифференциальное уравнение для v:

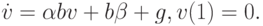
$ \dot {v} = \alpha {bv} + b\beta + g, v(1) = 0. $

Интегрируя эту задачу справа налево, попутно определяем u(t):

u(t) = \alpha (t) v(t) + \beta(t).

Метод дифференциальной прогонки оказывается весьма эффективным при решении линейных систем дифференциальных уравнений с переменными коэффициентами. Очевидно, что все приведенные выше соотношения верны без изменения и для таких систем.

Рассмотрим теперь общую постановку жесткой краевой задачи, неявно содержащую большой параметр. О жестких системах и задаче Коши для них речь шла в "Численные методы решения жестких систем обыкновенных дифференциальных уравнений" . Рассматривается линейная система

\begin{gather*} \frac{d{u}}{dt} = Au + F, t \in \left[{a, b}\right], \\ (D_i , u(a)) = \sum\limits_{s = 1}^{N}{d_{is}}u_{s} (a) = q_i , i = 1, \ldots , k, \quad k < N, \\ (D_i , u(b)) = \sum\limits_{s = 1}^{N}{d_{is}}u_{s} (b) = q_i , i = k + 1, \ldots , N, \end{gather*}

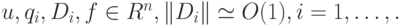
где u, q_i , D_i, f \in R^n, \left\|{D_i}\right\| \simeq O(1), i = 1, \ldots,.

Здесь \mathbf{A} — постоянная матрица размером N x N (дальнейшие рассуждения будут справедливы и для систем уравнений с переменными коэффициентами). Определители систем линейных алгебраических уравнений, которыми являются краевые условия на обоих концах интервала интегрирования, полагаются отличными от нуля.

Определение. Рассматриваемая краевая задача для ОДУ является жесткой, если спектр собственных значений матрицы \mathbf{A} можно разделить на три части.

  1. Левый жесткий спектр, для которого справедливо {\mathop{\mathrm{Re}}\nolimits} \Lambda_i^1 \le - \Lambda_0, \left|{{\mathop{\mathrm{Im}}\nolimits} \Lambda_i^1 }\right| < \Lambda _0, \Lambda_0 \gg 1, i = 1, \ldots , N_1.
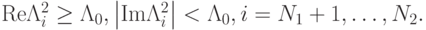
  2. Правый жесткий спектр, для которого {\mathop{\mathrm{Re}}\nolimits} \Lambda_i^2 \ge \Lambda_0, \left|{{\mathop{\mathrm{Im}}\nolimits} \Lambda_i^2 }\right| < \Lambda_0, i = N_1 + 1, \ldots , N_2 .
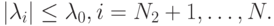
  3. Мягкий спектр \left|{\lambda_i}\right| \le \lambda_0, i = N_2 + 1, \ldots , N.

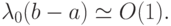
Отношение {{\Lambda_0 }/{\lambda_0 }} \gg 1 является параметром, характеризующим жесткость системы. В дальнейшем будем полагать \Lambda _0 (b - a) \gg 1, \lambda_0 (b - a) \simeq O(1).

Общее решение такой системы имеет вид

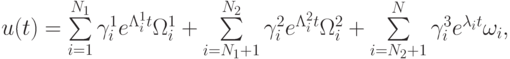
{u}(t) = \sum\limits_{i = 1}^{N_1 }{\gamma_i^1 e^{\Lambda_i^1t}{{\Omega }}_i^1 + \sum\limits_{i = N_1 + 1}^{N_2 }{\gamma_i^2 e^{\Lambda_i^2 t}{{\Omega }}_i^2 + \sum\limits_{i = N_2 + 1}^{N}{\gamma_i^3 {e}^{\lambda_it}} }}{{ \omega }}_i,

где \Omega_i^1, \Omega_i^2, \omega_i есть собственные векторы матрицы A, соответствующие трем частям спектра. Понятна качественная структура этого решения, содержащего как левый, так и правый пограничные слои. Будем полагать, что количество собственных значений в каждой из трех частей спектра не изменяется. Особенность жестких краевых задач состоит в том, что их решениями являются ограниченные функции. 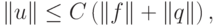Для них верно \left\|{{u}}\right\| \le C\left({\left\|f\right\| + \left\|{q }\right\|}\right), || f || и || q || - нормы правых частей в системе ОДУ и краевых условиях, соответственно. Для численного решения задачи можно использовать такую же схему второго порядка, как и ранее. Рассматриваем класс вычислительно корректных задач, для которых C = O(1) \ll \exp(\Lambda_0(b - a)).

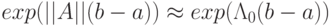В дальнейшем будем полагать величину ||A|| (b - a) \approx \Lambda _{0}(b - a) большой, а величину exp(||A|| (b - a)) \approx exp(\Lambda _{0}(b - a)) — очень большой. В приложениях такие задачи встречаются наиболее часто. Важно отметить и то, что не все возможные постановки задач для жесткой системы приводят к вычислительно корректным алгоритмам. Показывается, что необходимыми (и почти достаточными) условиями корректности являются следующие неравенства: 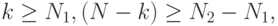k \ge N_1, (N - k) \ge N_2 - N_1, т.е. число краевых условий на левом конце отрезка интегрирования не должно быть меньше быстро убывающих вправо решений, на правом конце — не меньше быстро убывающих влево решений. В противном случае краевая задача оказывается вычислительно некорректной, так как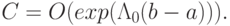 C = O(exp(\Lambda _{0}(b - a))).

Проблемы, которые возникают при численном решении жесткой краевой задачи, были уже рассмотрены: суммирование функций порядка eLt, как известно, приводит к потере точности и накоплению вычислительных ошибок. Вторая проблема состоит в следующем. Для вычисления коэффициентов 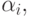\alpha_i, входящих в общее решение неоднородной системы (а оно состоит из суммы частного решения неоднородной системы и общего решения однородной 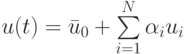u (t) = {\bar{u}}_0 + \sum\limits_{i = 1}^{N}{\alpha_i}u_i ), приходится решать плохо обусловленную СЛАУ (D_i, \bar{u}(b) + \sum\limits_i {\alpha_i}u_i(b)) = q_i, i = k + 1, \ldots,.

Дальше >>
< Лекция 10 || Лекция 11: 123456789

Вопросы и ответы

вопросов: 1
Sanjar Ibrohimov
Sanjar Ibrohimov
ответить