НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 11: Численное решение краевых задач для систем обыкновенных дифференциальных уравнений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский физико-технический институт

Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3791 / 1086 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00

ISBN: 978-5-9556-0065-9

Темы: Алгоритмы и дискретные структуры, Математика

Специальности: Программист, Математик

|

Вам нравится? Нравится 53 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

10.8. Решение краевой задачи методом Фурье

Рассмотрим разностную задачу

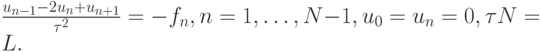
$\frac{{u_{n - 1} - 2u_n + u_{n + 1}}}{{\tau ^2 }} = - f_n , n = 1, \ldots , N - 1, u_0 = u_n = 0, \tau N = L .$

Построим ее решение в виде разложения по базису из собственных функций разностного оператора:

${P}^\tau (u) = \frac{{u_{n - 1} - 2u_n + u_{n + 1}}}{{\tau ^2 }}.$

Этот оператор имеет полную ортонормированную систему собственных функций

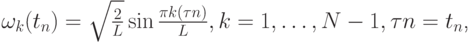
$$ \omega_k (t_n) = \sqrt {\frac{2}{L}} \sin \frac{{\pi k(\tau n)}}{L}, k = 1, \ldots , N - 1, \tau n = t_n $,$

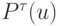которые соответствуют собственным значениям оператора $P^{\tau }(u)$ :

$$ \lambda_k = \frac{4}{\tau^2 }\sin ^2 \frac{\pi k\tau }{2L} $.$

Будем искать решение в виде

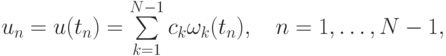
$u_n = u(t_n) = \sum\limits_{k = 1}^{N - 1}c_k \omega_k(t_n), \quad n = 1, \ldots , N - 1,$

где c_k — пока неизвестные коэффициенты Фурье. Для нахождения этих коэффициентов представим правую часть разностного уравнения в виде суммы Фурье

$f_n = \sum\limits_{k = 1}^{N - 1}{\hat f_k}\omega_k (t_n), \quad \mbox{где}\quad \hat f_k = (f, \omega_k) = \sum\limits_{i = 1}^{N - 1}f_i\omega_k(t_i)\tau.$

Подставим выражение для u_n, f_n в виде сумм Фурье в исходное разностное уравнение

$P^{\tau}[\sum\limits_{k = 1}^{N - 1}c_k \omega_k(t_n)] = - \sum\limits_{k = 1}^{N - 1}\widehatf_k \omega_k (t_n)$

или

$\sum\limits_{k = 1}^{N - 1}{c_k}{P}^\tau \left[{\omega_k(t_n)}\right] = - \sum\limits_{k = 1}^{N - 1}{\hat {f_k}}\omega_k (t_n),$

откуда, с учетом соотношения

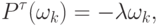
$P^{\tau }(\omega _{k}) = - \lambda \omega _{k},$

получим

$- \sum\limits_{k = 1}^{N - 1}{c_k} (\lambda_k \omega_k) = - \sum\limits_{k = 1}^{N - 1}{\hat f_k}\omega_k , c_k \lambda_k = \hat f_k , c_k = \frac{{\hat f_k}}{{\lambda_k}}.$

Таким образом, получено решение разностного уравнения в виде суммы Фурье. Несложные арифметические подсчеты показывают, что метод прогонки, требующий O(N) арифметических действий для численного решения этой же разностной задачи (из них 2(N - 1) умножений и N - 1 деление) оказывается более экономичным, чем метод Фурье, требующий O(N²) действий ( 2(N - 1)² умножений и N - 1 деление). Преимущества метода Фурье сказываются при решении двумерных разностных уравнений с постоянными коэффициентами.

10.9. Задачи

Пусть краевая задача имеет вид
${y^{\prime\prime} = f(x, y), y(0) = a, y(1) = b, }$ ( 10.3)

где нелинейная функция f не зависит явно от первой производной y'_x. В 1924 году Б.Нумеров предложил следующий метод аппроксимации задачи (10.3):

${y_{n + 1} - 2y_n + y_{n - 1} = h^2 [f_n + \frac{1}{{12}}(f_{n + 1} - 2f_n + f_{n - 1})], }$ ( 10.4)

где введено обозначение f_k = f(x_k, y_k).

В чем заключается отличие метода Нумерова от аппроксимации вида (10.5):

${y_{n + 1} - 2y_n + y_{n - 1} = h^2 f_n?}$ ( 10.5)

Описать алгоритмы численного решения нелинейных алгебраических систем (10.4) и (10.5). В случае (10.4) и f = f(x) это — алгоритм прогонки.

Решение. Выпишем главный член погрешности аппроксимации разностного уравнения (10.4). Для этого подставим в разностное уравнение проекцию на сетку точного решения задачи (10.3). Следует отметить, что конкретный вид решения не важен, достаточно только, чтобы решение существовало. Предположим также, что оно четырежды непрерывно дифференцируемо.

Раскладывая проекции точного решения в правой части (10.4) в ряд Тейлора до четвертого порядка включительно, убедимся, что все нечетные производные взаимно уничтожатся, а четные дадут следующее выражение для главного члена погрешности аппроксимации:

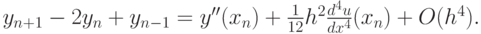
$y_{n + 1} - 2y_n + y_{n - 1} = y^{\prime\prime}(x_n) + \frac{1}{12}h^2 \frac{{d^4 u}}{{dx^4 }}(x_n) + O(h^4 ).$

Из уравнения (10.3) следует, что во всех внутренних точках области выполняется равенство

$y^{(4)} = \frac{{d^2 }}{{dx^2 }}f(x, y),$

переходя в последнем равенстве к разностной аппроксимации правой части, можно учесть явно главный член погрешности аппроксимации в (10.5). Приводя подобные слагаемые в (10.4), получаем аппроксимацию Нумерова

$y_{n + 1} - 2y_n + y_{n - 1} = \frac{h^2 }{12}(f_{n + 1} + 10f_n + f_{n - 1}),$

которая приближает исходную задачу во внутренних точках сеточной области с четвертым порядком.

Такая идея разумного распоряжения правой частью для неоднородных и нелинейных задач приводит к компактным (возможно, название не слишком удачное — термины "компакт" и "компактный" уже давно заняты в математике под совсем другое!) разностным схемам — схемам повышенного порядка точности на нерасширенном шаблоне. Действительно, и в элементарном шаге вычислений для (10.4) и (10.5) участвуют только три точки. Вопросам построения компактных разностных схем для нелинейных уравнений в частных производных посвящена монография [10.7].

В случае, когда правая часть явно зависит от первой производной, либо не получается компактной схемы, либо схема перестает быть экономичной. Действительно, чтобы не ухудшить порядок аппроксимации, необходимо вычислять значение первой производной в соответствующих узлах со вторым порядком. Если во всех точках использовать формулу с центральной разностью, то расширится шаблон схемы — в каждом шаге элементарных вычислений должно теперь участвовать пять точек. Если для точки с индексом n использовать формулу с центральной разностью, а для точек с индексами n + 1 и n - 1 — соответствующие формулы для односторонней производной, то для каждой точки шаблона придется вычислять заново значения функции f. При использовании классического вида аппроксимации Нумерова при каждом элементарном вычислении производится лишь однократное обращение к функции вычисления правой части — лишь для f_{n + 1}, значения f_n и f_{n - 1} уже получены при вычислениях для точки с индексом n - 1. Так как время вычислений, как правило, определяется в таких задачах именно количеством обращений к правой части, то вычисления замедляются в три раза.
Для численного отыскания периодического с периодом "единица" решения уравнения
```
y'' + p(x)y' + q(x)y = f(x)
```
где f, q, p — заданные функции, используется разностная схема.

Предложить модификацию метода прогонки (периодическая прогонка) для решения данной задачи.

Решение. Рассмотрим следующую краевую задачу для уравнения Штурма - Лиувилля
```
y'' + p(x)y' + q(x)y = f(x)
```
с условиями периодичности
```
y^(p)(0) = y^(p)(1),
```
где p принимает значения 0 и 1. Отметим, что пока период решения считается известным. Отрезок [0, 1] возможно рассматривать без ограничения общности, так как любой отрезок можно перевести в единичный неособым линейным преобразованием, при этом вид уравнения существенно не изменится (функции p и q умножатся на постоянный множитель).

Краевая задача с условиями периодичности решается методом циклической прогонки. Запишем дискретный аналог уравнения:

$\frac{y_{n + 1} - 2y_n + y_{n - 1}}{h^2 } + p_n \frac{y_{n + 1} - y_{n - 1}}{2h} + q_n y_n = f_n .$

Очевидно, что оно аппроксимирует дифференциальную задачу со вторым порядком на равномерной сетке. На случай неравномерной сетки рассматриваемый метод легко обобщается.

В силу периодичности дискретное уравнение должно выполняться во всех точках сетки, включая граничные. Кроме того, в силу граничного условия при p = 0, y₀ = y_{N + 1}, система сеточных соотношений примет вид:

$\begin{gather*} a_0 y_n - b_0 y_0 + c_0 y_1 = \varphi_0 , \\ \ldots , \\ a_n y_{n - 1} - b_n y_n + c_n y_{n + 1} = \varphi_n , \\ \ldots , \\ a_n y_{N - 1} - b_n y_n + c_n y_0 = \varphi_n , \end{gather*}$

где $a_k = 1 - 0, 5p_k h, b_k = 2 - q_k h^2, c_k = 1 + 0, 5p_k h, \varphi_k = f_k h^2 .$ Матрица системы линейных уравнений получается "почти трехдиагональной" — от трехдиагональной ее отличают всего два элемента в углах матрицы.

Обобщение стандартных прогоночных соотношений (для трехточечной прогонки) на периодический случай будет иметь вид

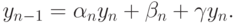
Из приведенного выше соотношения для y₀ сразу получаем, что 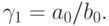$\alpha_1 = {{c_0 }/ {b_0, }}$ $\beta_1 = - {{f_0 }/{b_0 }},$ $\gamma _{1} = a_{0}/ b_{0}.$ Теперь несложно получить рекуррентную зависимость для прогоночных коэффициентов: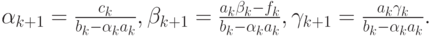

$\alpha_{k + 1} = \frac{c_k}{b_k - \alpha_k a_k}, \beta_{k + 1} = \frac{a_k \beta_k - f_k}{b_k - \alpha_k a_k}, \gamma_{k + 1} = \frac{a_k \gamma_k}{b_k - \alpha_k a_k}.$

По приведенным выше формулам получаются значения коэффициентов для всех уравнений с номерами меньше, чем n. Подставим теперь прогоночные соотношения в последнее уравнение линейной системы. В итоге с учетом введенных выше обозначений получаем

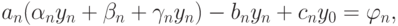
а это соотношение, сгруппировав члены, можно переписать как:

$y_{n} = \mu _{n}y_{0} + \eta _{n},$

где введены обозначения

$\mu_n = \frac{- c_n}{a_n(\alpha_n + \gamma_n) - b_n}, \eta_n = \frac{\varphi_n - a_n \beta_n}{a_n (\alpha_n + \gamma_n) - b_n}.$

Теперь выражение для значения сеточной функции y_{n - 1} подставляем в прогоночные соотношения. Получается выражение, связывающее y_{n - 1} с y₀:

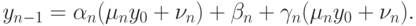
Отсюда получаем следующие рекуррентные соотношения:

Отметим, что эти коэффициенты вычисляются в обратном порядке — аналог обратного хода прогонки. Последнее соотношение приводит к явному выражению для y₀. В результате получаем

$y_0 = \frac{\eta_0 }{1 - \mu_0 }.$

Теперь информации для определения значений искомой функции во всех точках сетки (еще один ход прогонки) достаточно.

Алгоритм периодической прогонки был предложен А.А.Абрамовым.