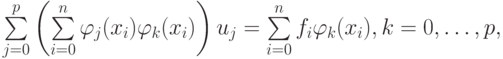Московский физико-технический институт
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 3968 / 1245 | Оценка: 4.50 / 4.33 | Длительность: 24:00:00
ISBN: 978-5-9556-0065-9
Специальности: Программист, Математик
Теги:
Лекция 4:
Численное решение переопределенных СЛАУ. Метод наименьших квадратов
Аннотация: В лекции рассматриваются методы решения переопределенных систем уравнений. Обсуждается вопрос о выборе базиса на погрешность результата. Вкратце
описываются итерационные методы решения плохо обусловленных систем линейных
уравнений.
Ключевые слова: переопределенная система, функция, коэффициенты, прямой, значение, невязки, вес, метод наименьших квадратов, базис, выражение, обобщенный полином, производные, матрица, обобщенный многочлен, конечный ряд Фурье, скалярное умножение, ранг, минимум, равенство, базисные функции, эквивалентность, Произведение, вектор, произведение вектора, симметричность, эквивалентная система
3.1. Пример использования метода наименьших квадратов (МНК)
Приведем простой пример получения переопределенной системы линейных уравнений. Такого рода задачи часто встречаются, например, при обработке результатов экспериментов.
Пусть f — линейная (или близкая к линейной) функция аргумента x: f(x) = u1x + u0. В точках xk известны значения функции f(xk). Тогда u0, u1 — коэффициенты, которые необходимо подобрать так, чтобы выполнялись условия u1xk + u0 = fk, k = 0,1,2,3,4, fk = f(xk).
Получим систему пяти уравнений относительно двух неизвестных. Это — переопределенная система. Она не имеет классического решения, так как в общем случае не существует прямой, проходящей через все 5 точек (это возможно только тогда, когда какие - либо три уравнения полученной системы линейными преобразованиями сводятся к двум другим — система линейно зависима).
Рассмотрим общий случай. Пусть коэффициенты {u0, u1} необходимо определить по результатам n + 1 измерения. Введем функцию, равную сумме квадратов невязок rk = u1xk + u0 - fk
 |
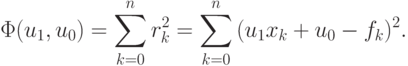( 3.1) |
Примем за обобщенное решение переопределенной СЛАУ такие {u0,
u1} для которых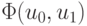 
принимает наименьшие значение. Для определения обобщенного решения из условия минимума суммы квадратов невязки получаем систему двух уравнений, имеющую классическое решение:
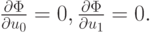
Выбор функции 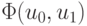имеет некоторый произвол. Например, возможно каждому измерению придать некоторый вес bk. От набора таких весовых множителей зависело бы решение системы. В этом случае функция 
будет
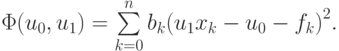
Если в качестве невязки выбрать rk = | u1xk + u0 - fk |, то получим задачу линейного программирования на отыскании минимума функции
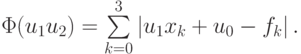
Получившийся таким образом функционал, вообще говоря, не дифференцируем. Для решения задачи нельзя использовать метод наименьших квадратов.
Произвол имеется и в выборе базисных функций. Вообще говоря, можно было бы записать невязку rk в виде
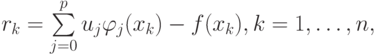
где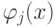 
— некоторые функции, образующие базис, например, тригонометрические: 
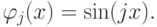Выражение 
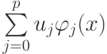называется обобщенным полиномом. В приведенном выше примере в качестве базисных функций были
выбраны степенные функции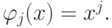 
Обобщенный полином превратился в алгебраический.
В случае выбора произвольной системы базисных функций переопределенная СЛАУ
и функционал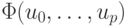 
будут
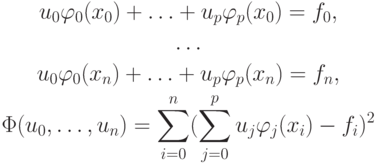
Отыщем обобщенное решение методом наименьших квадратов. Приравнивая все частные производные по компонентам обобщенного решения к нулю
